CHƯƠNG 1. CC KIN THC CƠ S
1.1. Các khái niệm cơ bản
1.2. Lý thuyết tổ hợp
1.3. Hai nguyên lý cơ bản
1.4. Lý thuyết số và các hệ đếm
1.5. Bài tập
1.1. CC KHI NIM CƠ BN
1. Logic mệnh đề.
2. Logic vị từ.
3. Các phương pháp chứng minh.
4. Tập hợp và hàm.
5. Ma trận và giải thuật.
LOGIC MNH Đ
a) Mệnh đề, mệnh đề có điều kiện và sự tương đương logic.
b) Dạng chuẩn tắc hội và chuẩn tắc tuyển của công thức.
c) Các phương pháp kiểm tra tính hằng đúng, hằng sai của công thức.
MNH ĐÊ(1/3)
Mệnh đề là câu có giá trị hoặc đúng hoặc sai; nhưng không thể vừa
đúng vừa sai hoặc không thể khẳng định tính đúng, sai của nó.
Ví dụ 1:
"6 là một số chẵn”
“Hà Nội là thủ đô của Việt Nam”
“3+2 = 6”
Ví dụ 2: Những câu không là mệnh đề
“x là một số chẵn”
“Kinh tế Mỹ khi nào phục hồi”
“Trật tự”
MNH ĐÊ(2/3)
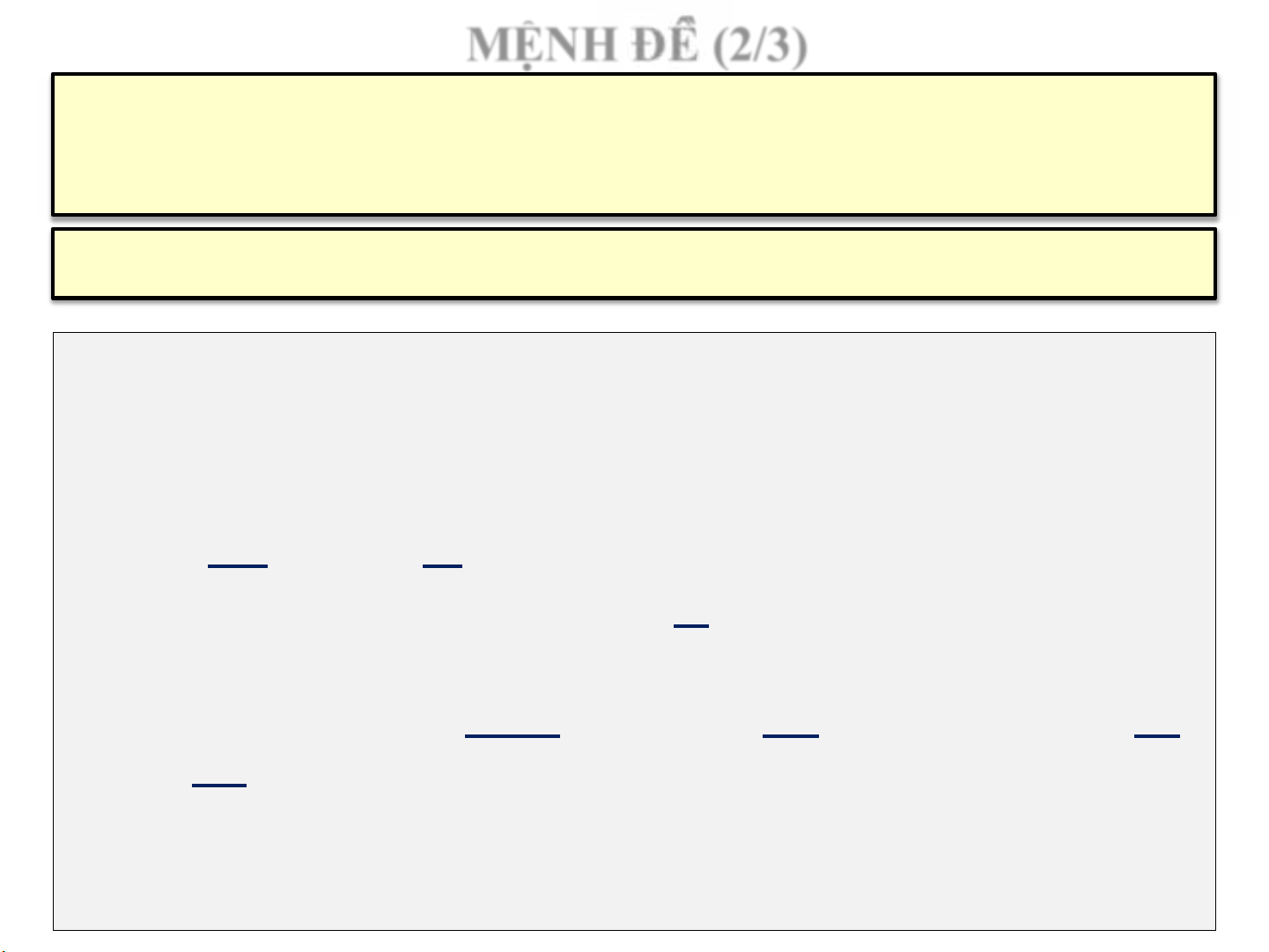
Mệnh đề không chứa các liên từ "và", "hoặc", "không", "nếu... thì..." được
gọi là mệnh đề nguyên thủy hay mệnh đề sơ cấp.
Ví dụ 3:
1) "6 là một số chẵn”
2) “Tôi là tổng thống Mỹ”
3) “Nếu trời nắng thì tôi đi chơi”
4) “Hà Nội là thủ đô của Việt Nam và Thành phố HCM là trung tâm
kinh tế lớn nhất Việt Nam”
5) “Người đi xe máy không vượt đèn đỏ nếu anh ta thấy công an trừ
khi anh ta quá liều”
1), 2) là mệnh đề sơ cấp.
3), 4), 5), 6) là các mệnh đề phức hợp
Mệnh đề không phải là mệnh đề sơ cấp được gọi là mệnh đề phức hợp.