CÂY
ntsonptnk@gmail.com
Đ NH NGHĨAỊ
•CÂY là đ th liên thông và không ồ ị
có chu trình
•R NG là m t đ th g m p thành Ừ ộ ồ ị ồ
ph n liên thông, trong đó m i ầ ỗ
thành ph n liên thông là m t câyầ ộ
•L u ýư: cây không ch a khuyên và ứ
c nh song song.ạ
Lý thuy t đ th - ch ng 2 – Nguy n Thanh S nế ồ ị ươ ễ ơ
C
AB
D
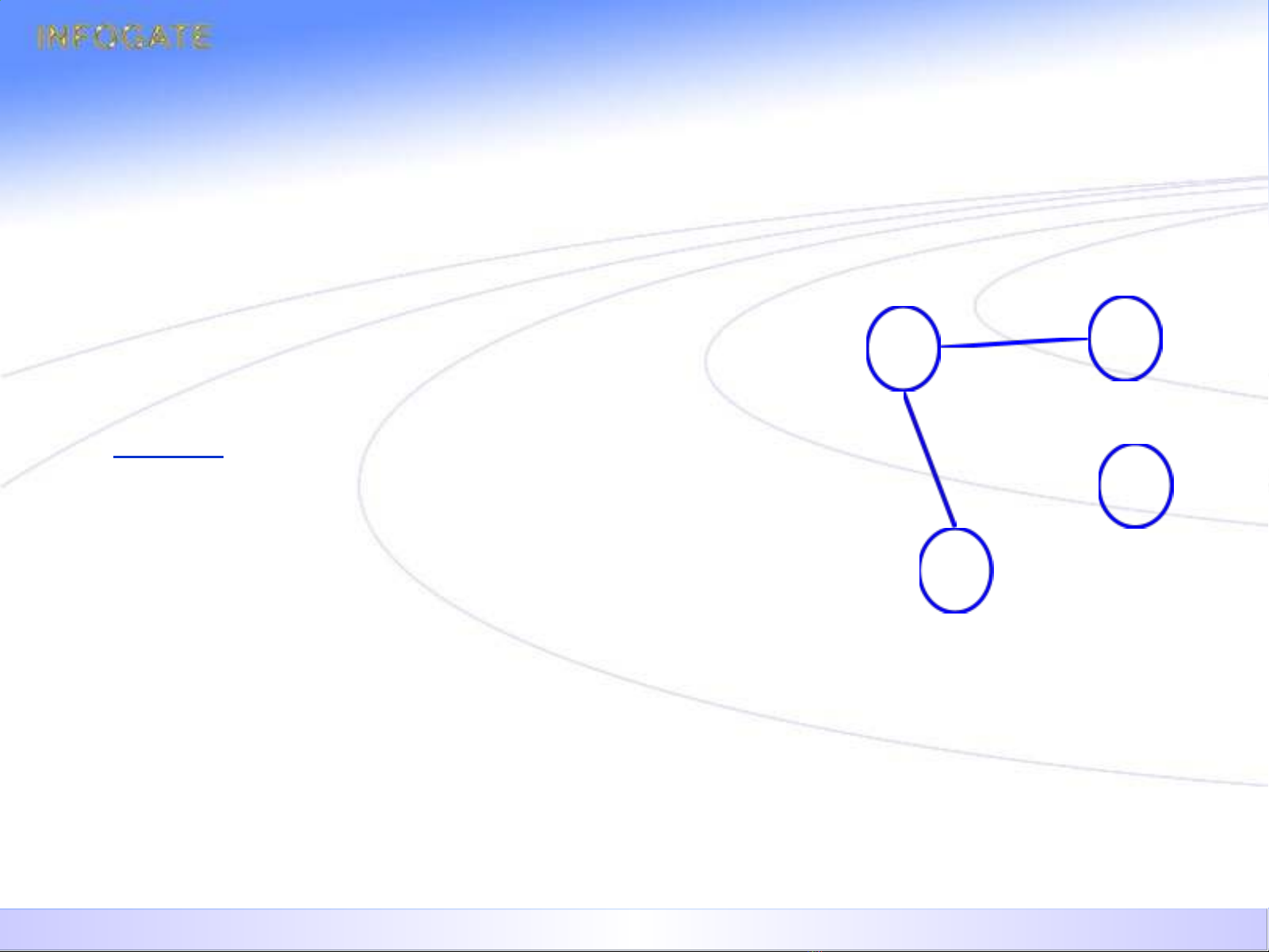
S T N T I Đ NH TREOỰ Ồ Ạ Ỉ
Đ nh lý: ịM t cây T g m N đ nh v i N 2 ch a ít nh t hai ộ ồ ỉ ớ ứ ấ
đ nh treo ỉ
Lý thuy t đ th - Nguy n Thanh S nế ồ ị ễ ơ
C
AB
D
E
F
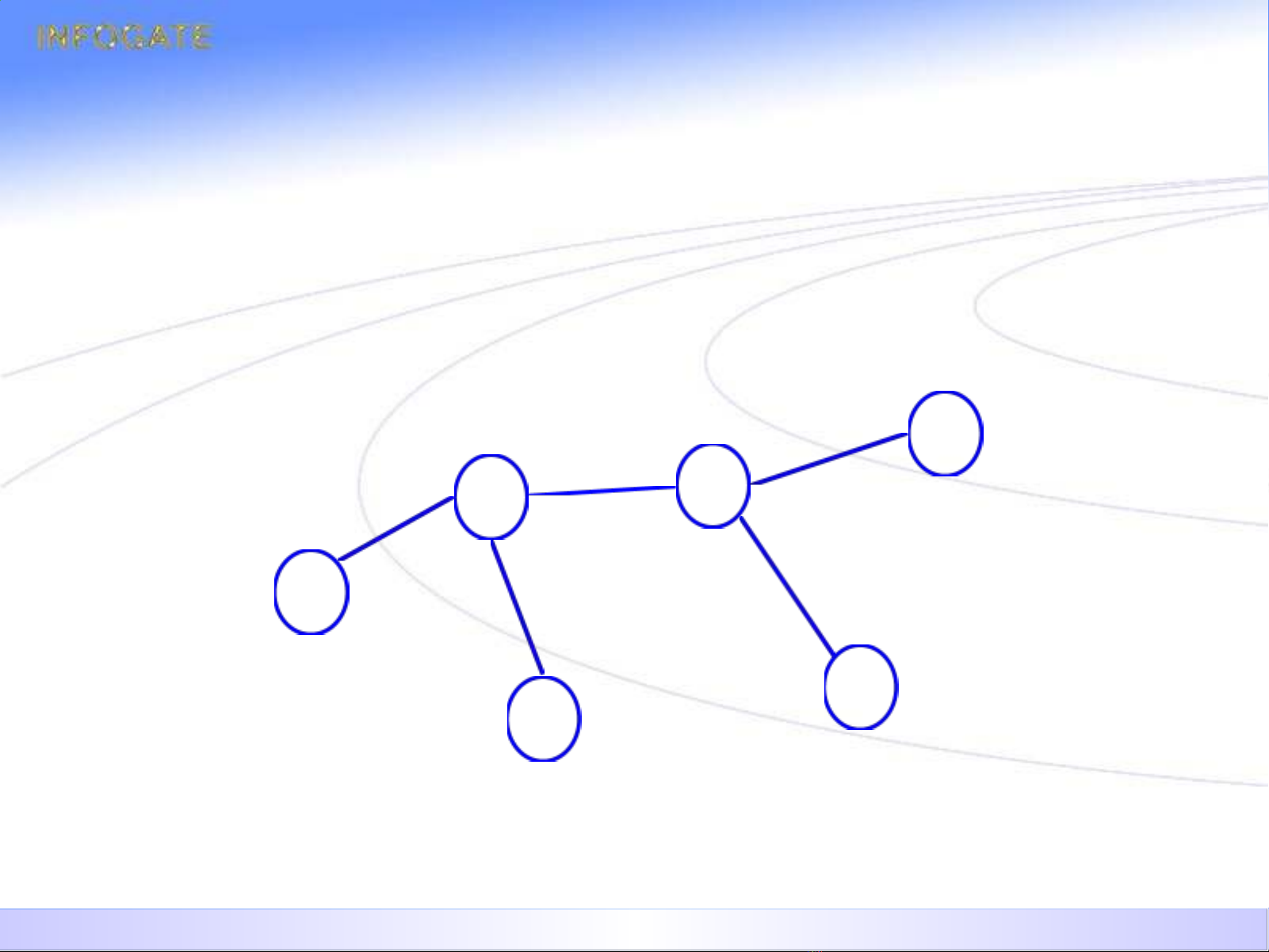
CÁC Đ NH NGHĨA T NG Đ NGỊ ƯƠ ƯƠ
Xét đ th G g m N đ nh, các đi u sau đây t ng đ ng.ồ ị ồ ỉ ề ươ ươ
1.Đ th G là cây.ồ ị
–Gi a hai đ nh b t kỳ c a G, t n t i duy nh t m t dây ữ ỉ ấ ủ ồ ạ ấ ộ
chuy n n i chúng v i nhau.ề ố ớ
–G liên thông t i ti u.ố ể
–Thêm m t c nh n i 2 đ nh b t kỳ c a G thì G s ch a ộ ạ ố ỉ ấ ủ ẽ ứ
m t chu trình duy nh t.ộ ấ
–G liên thông và có n-1 c nhạ
–G không có chu trình và có n-1 c nhạ
Lý thuy t đ th - Nguy n Thanh S nế ồ ị ễ ơ
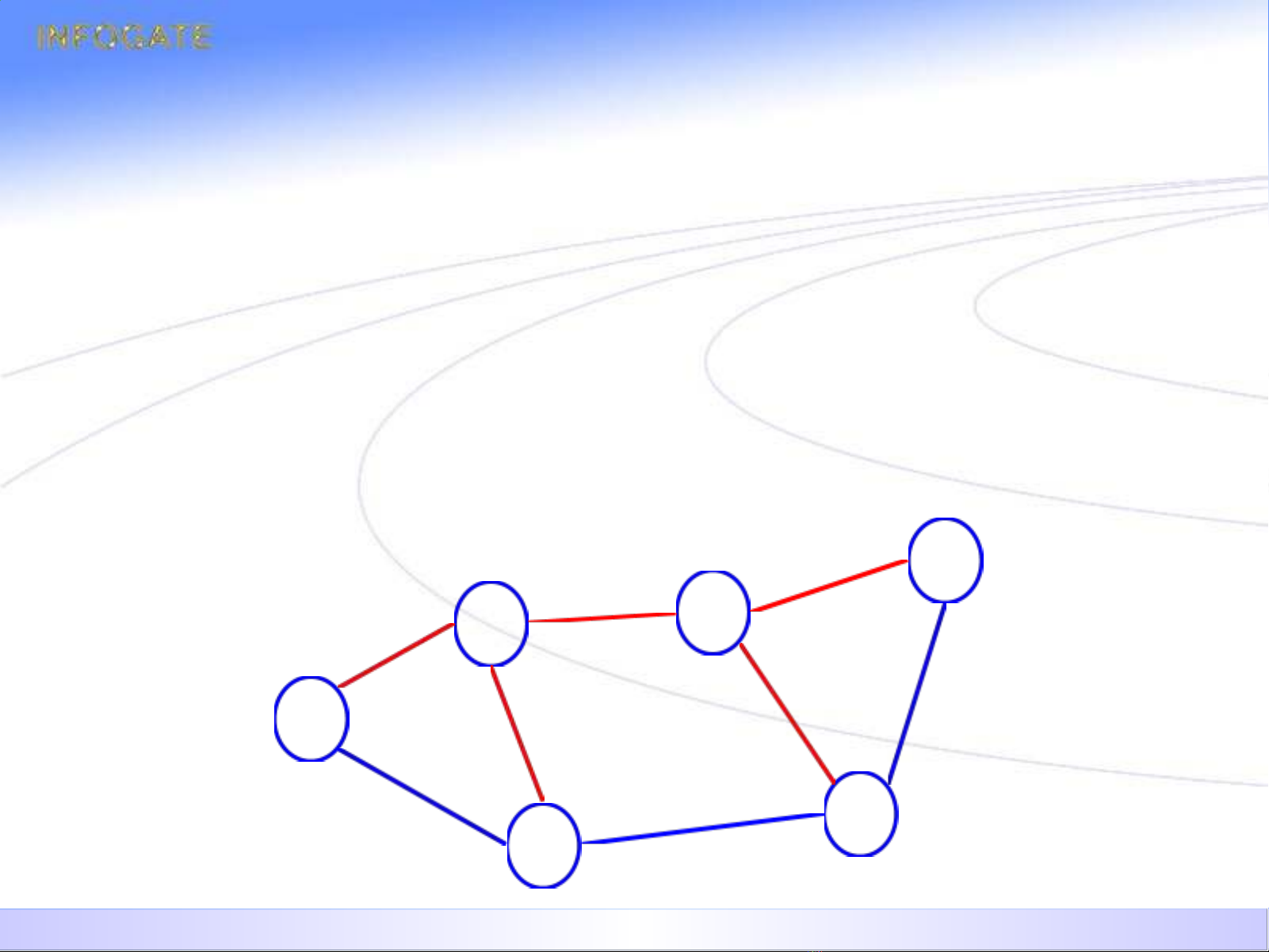
CÂY T I Đ IỐ Ạ
•Đ nh nghĩa: ịCho G=(X, E) là m t đ th liên thông và ộ ồ ị
T=(X, F) là m t đ th b ph n c a G. N u T là cây thì T ộ ồ ị ộ ậ ủ ế
đ c g i là m t cây t i đ i c a G.ượ ọ ộ ố ạ ủ
•Các tên g i khác: cây khung, cây bao trùm, cây phọ ủ
Lý thuy t đ th - Nguy n Thanh S nế ồ ị ễ ơ
C
AB
D
E
F