LÝ THUYẾT
XÁC SUẤT VÀ THỐNG KÊ TOÁN HỌC
Phan Văn Tân
Bộmô Khí tượng
CHƯƠNG 4. HỆCÁC ĐẠI LƯỢNG NGẪU NHIÊN
4.1 Khái niệm
• Khi giải quyết nhiều bài toán người ta thường gặp tình
huống là kết quảthí nghiệm được mô tảbởi một số (>1)
đại lượng ngẫu nhiên
•Khi đóta nói cómột “hệcác đại lượng ngẫu nhiên”
• Các tính chất của hệ đại lượng ngẫu nhiên không được
mô tảhết bởi những tính chất của các đại lượng ngẫu
nhiên riêng rẽ, chúng còn bao hàm cảnhững mối quan
hệ tương hỗgiữa các đại lượng ngẫu nhiên của hệ
•Giảsửxét đồng thời hai đại lượng ngẫu nhiên X và Y,
khi đómỗi cặp giá trịcó thểcủa X và Y được xem như
các tọa độ của một điểm ngẫu nhiên trong mặt phẳng
CHƯƠNG 4. HỆCÁC ĐẠI LƯỢNG NGẪU NHIÊN
4.1 Khái niệm
•Tương tự, nếu có ba đại lượng ngẫu nhiên X, Y, Z khi đó
mỗi bộba giá trịcó thểcủa X, Y, Z sẽlà các tọa độ của
một điểm ngẫu nhiên trong không gian ba chiều
•Nếu có đồng thời n đại lượng ngẫu nhiên X1, X2,…,Xn
thì bộngiá trịcó thể(x1, x2,…, xn) của X1, X2,…,Xnlà
tọa độ của điểm ngẫu nhiên trong không gian nchiều
•Vìvậy, có thểxem hệcác đại lượng ngẫu nhiên như là
biến ngẫu nhiên nhiều chiều hoặc vectơ ngẫu nhiên
•Nếu các đại lượng ngẫu nhiên thành phần là rời rạc ta có
hệcác đại lượng ngẫu nhiên rời rạc, ngược lại ta có hệ
các đại lượng ngẫu nhiên liên tục
CHƯƠNG 4. HỆCÁC ĐẠI LƯỢNG NGẪU NHIÊN
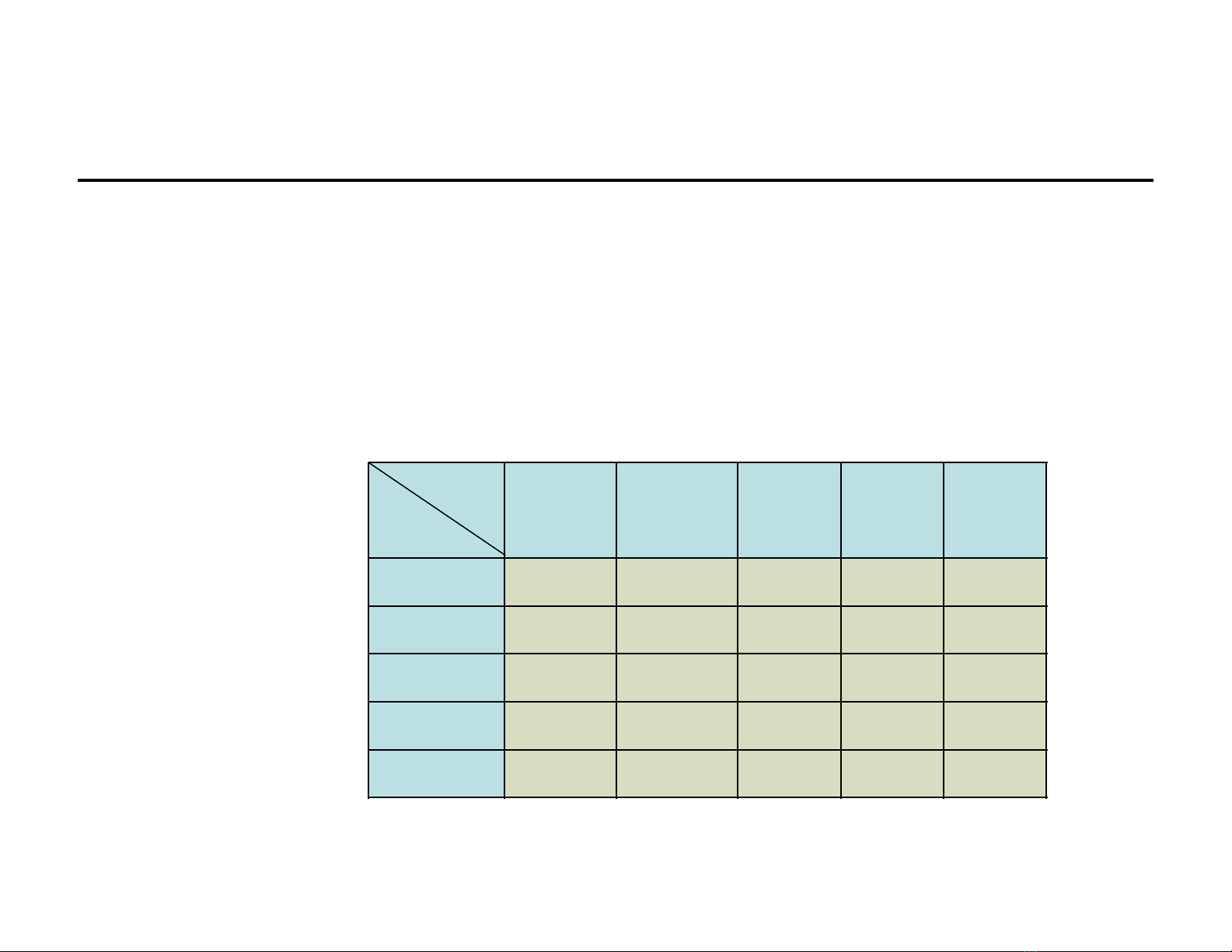
4.2 Hệ hai đại lượng ngẫu nhiên rời rạc. Bảng phân bốxác suất
•Xét hệ hai đại lượng ngẫu nhiên (X, Y), trong đócảX và Y đều là
những đại lượng ngẫu nhiên rời rạc, với
X={xi, i=1,2,…, n,…}, Y={yj, j=1, 2,…, m,…}
• Ký hiệu pi=P(X=xi), qj=P(Y=yj), pij=P(X=xi, Y=yj)
……………
...
…
…
…
pnm
…pn2
pn1
…………
p2m
…p22
p21
p1m
…p12
p11
…
…
xn
…
x2
x1
ym
…y2
y1
Y
X
Bảng phân bố
xác suất của
hệ hai đại
lượng ngẫu
nhiên rời rạc
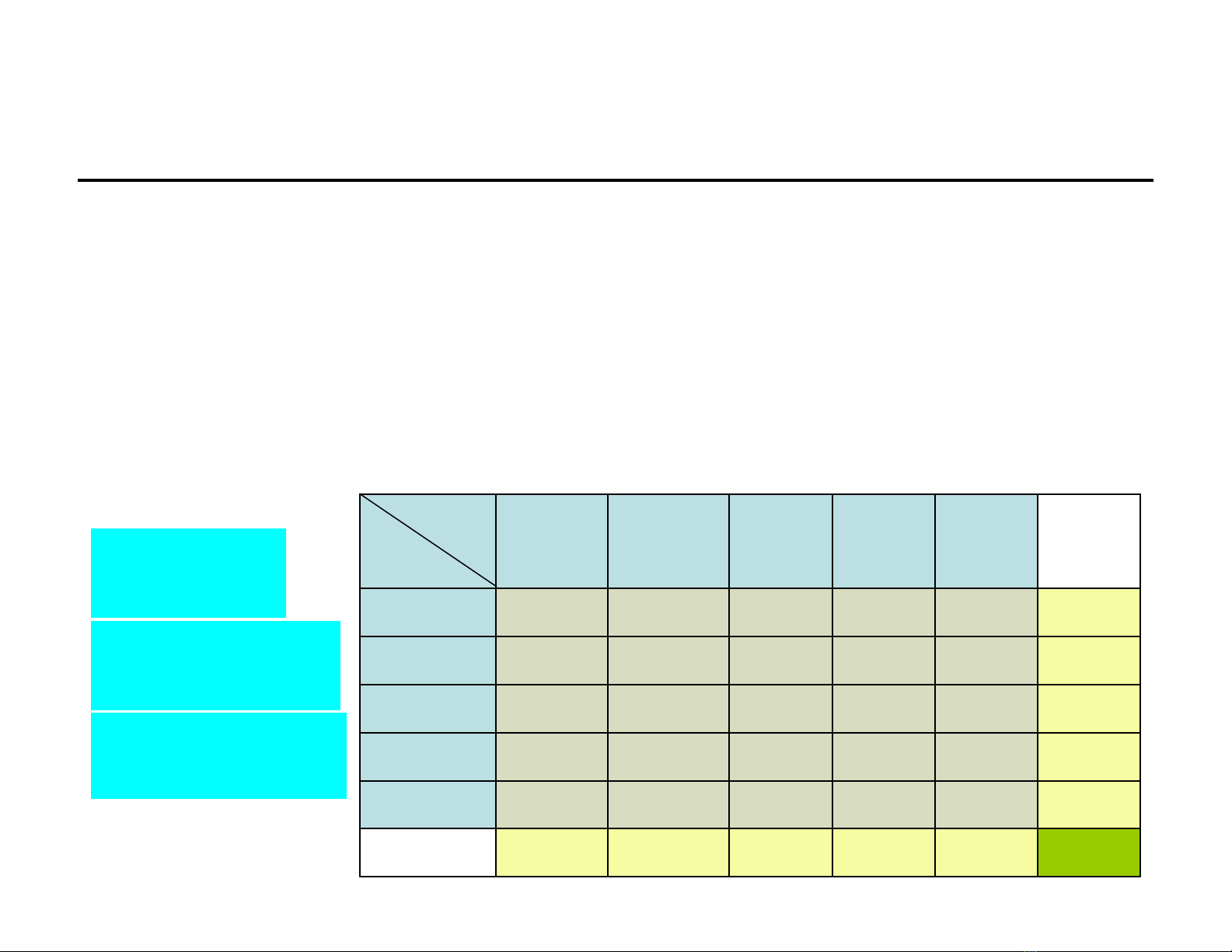
CHƯƠNG 4. HỆCÁC ĐẠI LƯỢNG NGẪU NHIÊN
4.2 Hệ hai đại lượng ngẫu nhiên rời rạc. Bảng phân bốxác suất
•Nhận thấy: Các sựkiện (X=xi) xung khắc, (Y=yj) xung khắc
•ÎCác sựkiện (X=xi)(Y=yj) là nhóm đầy đủ các sựkiện xung
khắc nên Σpij = 1
•(X=x
i)=Σj (X=xi)(Y=yj) ÎP(X=xi)=P(Σj (X=xi)(Y=yj))=pi≡pi•
•(Y=y
j)=Σi (X=xi)(Y=yj) ÎP(Y=yj)=P(Σi (X=xi)(Y=yj))=qj≡p•j
1
…
p•m
…p•2
p•1
∑
……………
...
…
…
…
pnm
…pn2
pn1
…………
p2m
…p22
p21
p1m
…p12
p11
…
pn•
…
p2•
p1•
∑
…
…
xn
…
x2
x1
ym
…y2
y1
Y
X
1=
∑∑
ij
ij
p
•
≡=
∑ii
j
ij ppp
jj
i
ij pqp •
≡=
∑