Mật mã ứng dụng
Mã dòng
1 / 34
Tài liệu
•Khóa học "Computer and Network Security"của Ron Rivest
•Khóa học "Crypto 1"của Dan Boneh
2 / 34
Nội dung
1Mã hóa
2One-time Pad
3Mã dòng
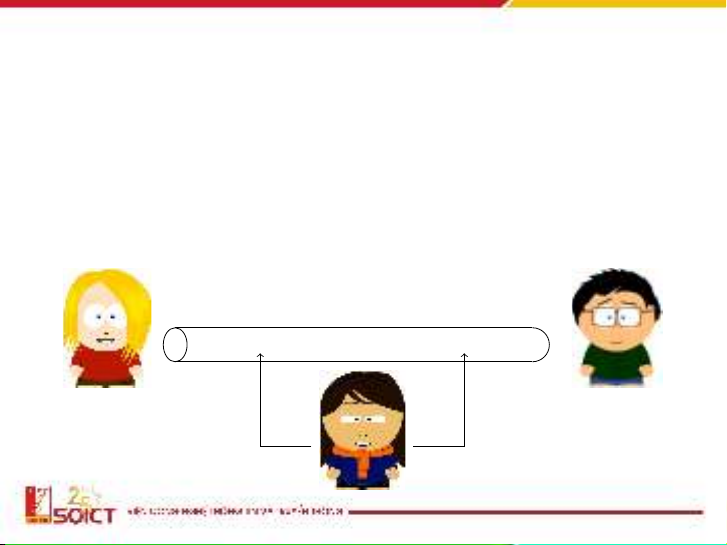
Mã hóa
Mục tiêu: Đảm bảo tính bí mật cho các thông điệp được gửi đi
(hoặc lưu trữ).
Nhân vật tham gia trò chơi:
•Alice, Bob là người “tốt”
•Eve là kẻ “nghe trộm”,“tấn công”
Alice Bob
Eve
Lắng nghe Sửa đổi
Kênh truyền không an toàn
4 / 34
Cách tiếp cận của mật mã
Alice Bob
Eve
Lắng nghe Sửa đổi
Kênh truyền không an toàn
•Bob biết khóa Kmà Eve không biết.
•Alice có thể mã hóa thông điệp Msao cho người biết khóa K
có thể giải mã.
•Eve có bản mã, nhưng không biết thông tin gì về M.
5 / 34