Bài giảng Nền móng: Chương 3 - PGS.TS Nguyễn Hồng Nam

Chia sẻ: Nguyễn Thị Ngọc Lựu | Ngày: | Loại File: PDF | Số trang:13

Thêm vào BST

Báo xấu

269
lượt xem 67
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Nền móng - Chương 3: Tính toán móng mềm, giới thiệu khái niệm móng mềm và mô hình nền, tính móng băng theo mô hình nền biến dạng cục bộ, tính móng băng theo mô hình nền biến dạng tuyến tính. Đây là tài liệu tham khảo cho sinh viên ngành Xây dựng.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Nền móng: Chương 3 - PGS.TS Nguyễn Hồng Nam

Chương 3 Tính toán móng mềm Nguyễn Hồng Nam, 2010 183 Nội dung • Khái niệm về móng mềm và mô hình nền • Tính móng băng theo mô hình nền biến dạng cục bộ • Tính móng băng theo mô hình nền biến dạng tuyến tính Nguyễn Hồng Nam, 2010 184
Khái niệm về móng mềm và mô hình nền • Căn cứ vào độ cứng của móng chia móng cứng và móng mềm. • Móng mềm chỉ liên quan đến móng có độ cứng hữu hạn (EJ≠0). • Không xét móng có độ cứng rất lớn (EJ=∞) hoặc độ cứng rất nhỏ (EJ=0). • Mục đích tính toán móng mềm là xác định phản lực nền và độ võng của dầm, từ đó xác định được nội lực trong dầm. Nguyễn Hồng Nam, 2010 185 Sự khác nhau chủ yếu về tính toán móng cứng và móng mềm • Đối với móng cứng lớn, bản thân móng bị biến dạng rất nhỏ, và coi như không ảnh hưởng đến sự phân bố phản lực nền, không phát sinh nội lực trong móng. • Đối với móng mềm, độ cứng của móng có ảnh hưởng đến sự phân bố phản lực nền và nội lực móng. • Chú ý: Khi tính toán móng mềm, xác định phản lực theo công thức nén lệch tâm sẽ có sai số lớn. Nguyễn Hồng Nam, 2010 186
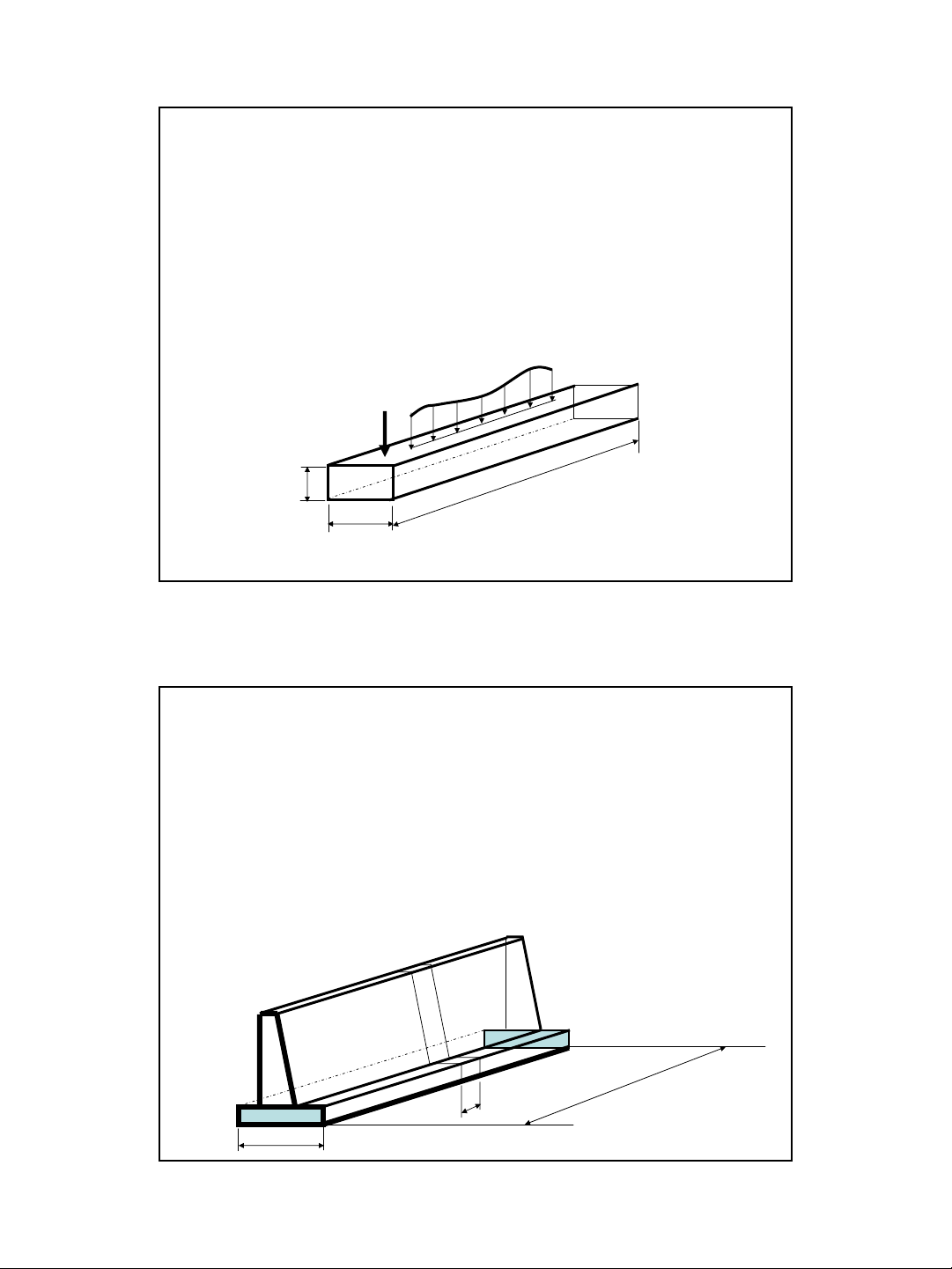
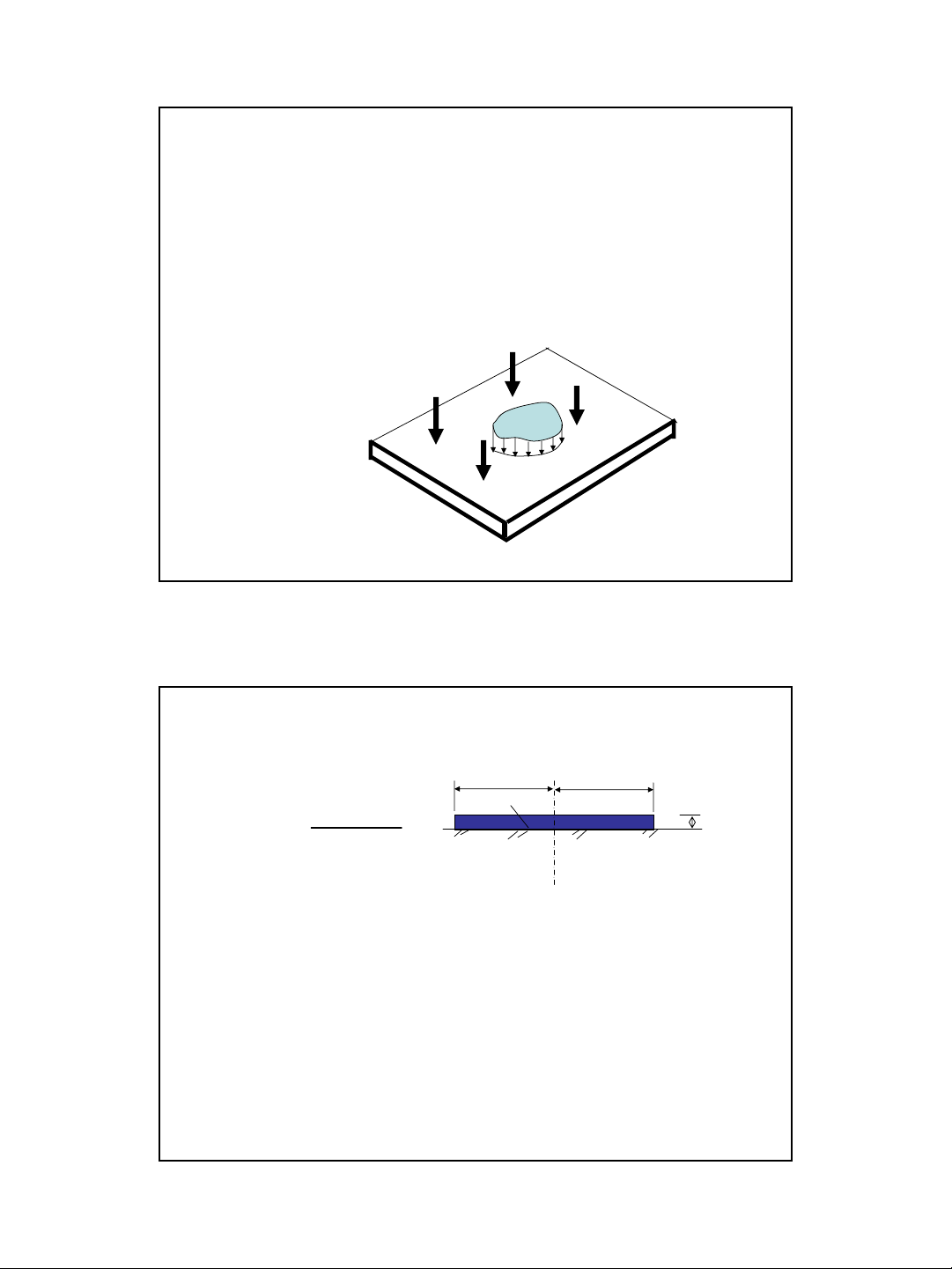
3 loại kết cấu móng mềm • Dầm: là móng có một kích thước (chiều dài) lớn hơn nhiều hai kích thước còn lại. Vì chiều rộng b nhỏ nên giả thiết trạng thái ứng suất biến dạng của dầm không biến đổi theo phương ngang bài toán ứng suất phẳng. L h b DẦM Nguyễn Hồng Nam, 2010 187 3 loại kết cấu móng mềm • Dải: là móng kéo dài vô hạn theo một phương. Tiết diện ngang và quy luật phân bố tải trọng không đổi theo phương đó. Chỉ cần xét bài toán biến dạng phẳng (cắt 1 m dài) vì biến dạng theo phương dài vô hạn bằng 0. • Đối với CTTL: xét chiều dài ≥ 3 lần chiều rộng, ví dụ: đê,đường. l>>b l l=1m DẢI 188 b Nguyễn Hồng Nam, 2010
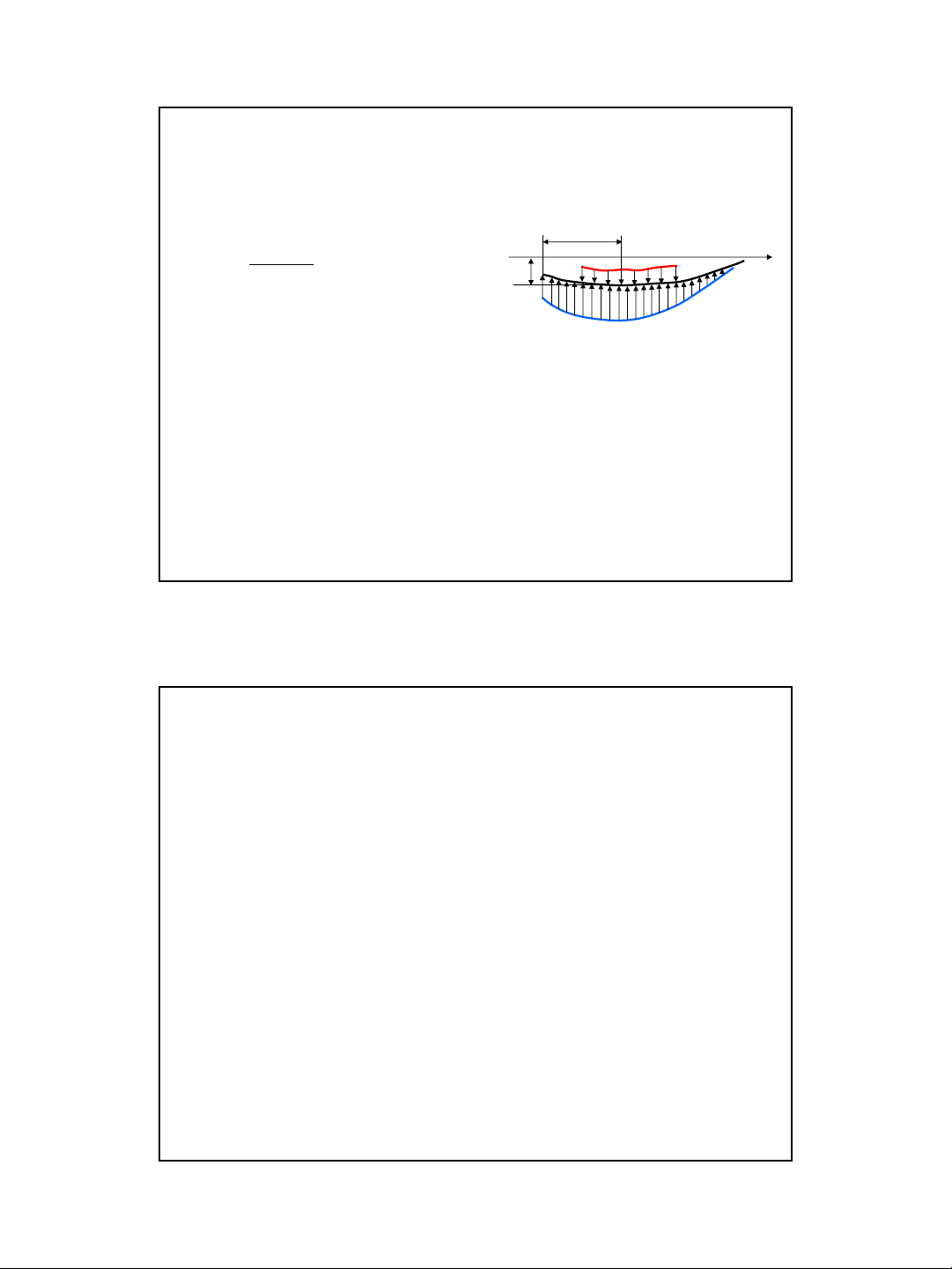
3 loại kết cấu móng mềm • Tấm (bản): là móng có hai kích thước mặt bằng cùng một cấp lớn. Trạng thái ứng suất biến dạng biến đổi theo cả hai phương. P1 P4 q P2 TẤM P3 (BẢN) Nguyễn Hồng Nam, 2010 189 Chỉ số độ mảnh l l 3 10 Eo l E t= h Eh 3 Eo • E: Mô đun đàn hồi của vật liệu móng • Eo: Mô đun biến dạng của đất nền. • l, h: Nửa chiều dài và chiều cao của móng. • Móng cứng: t
Khái niệm về mô hình nền • Mô hình nền là mô hình cơ học mô tả tính biến dạng của nền dưới tác dụng của ngoại lực. x d 4 w( x) x EJ = q ( x) − p( x) w(x) q(x) dx 4 p(x) • q(x): tải trọng phân bố bên ngoài tác dụng lên mặt nền • p(x): phản lực nền ẩn số • w(x): độ võng của móng (chuyển vị theo phương thẳng đứng) ẩn số • Pt có 2 ẩn nên không giải được biến dạng của dầm và nội lực của nó không những phụ thuộc tải trọng ngoài và độ cứng của dầm mà còn phụ thuộc tính biến dạng của nền nữa. • Điều kiện tiếp xúc: móng và nền cùng làm việc, luôn tiếp xúc với nhau, w(x)=S(x) • Cần thiết lập mối quan hệ thứ hai, thể hiện độ lún của mặt nền với áp lực đáy móng, tức là S ( x) = F [ p( x)] p( x) = F [ S ( x)] Nguyễn Hồng Nam, 2010 1 2 191 Khái niệm về mô hình nền • Hiện nay có 3 mô hình nền phổ biến là: Mô hình nền biến dạng cục bộ, Mô hình nền nửa không gian biến dạng tuyến tính, và Mô hình lớp không gian biến dạng tổng thể Nguyễn Hồng Nam, 2010 192
Mô hình nền biến dạng cục bộ (Mô hình Winkler) p(x) = c.S(x) • Giả thiết áp suất trên mặt nền tỷ lệ bậc nhất với độ võng của nền. • c: hệ số tỷ lệ, gọi là hệ số nền, thứ nguyên là p/chiều dài • Đối với dầm có chiều rộng b: p(x)=b.c.S(x) • Mô hình đơn giản • Mô hình có tính chất cục bộ (các lò xo độc lập với nhau) không phản ánh tính phân phối của đất (đặc tính huy động vùng đất xung quanh vào cùng làm việc với phần đất ngay dưới tải trọng). • Hệ số c không có ý nghĩa vật lý rõ ràng, nó không phải là hằng số đối với từng loại đất. Nguyễn Hồng Nam, 2010 193 Mô hình nền nửa không gian biến dạng tuyến tính • Nền đất được xem như bán không gian biến dạng tuyến tính (Eo, µo) • Lời giải Bousinessq (bài toán không gian) P d P (1 − µ o ) 2 S= (3-5) πEo d s • Trong đó: • Eo, µo: mô đun biến dạng và hệ số nở hông của nền. • P: tải trọng tác dụng tập trung • d: khoảng cách từ điểm đang xét đến điểm lực tác dụng • S: độ lún của nền • Nguyễn Hồngđộ lún mặt nền là một đường Hyperbol. Dạng Nam, 2010 194
Mô hình nền nửa không gian biến dạng tuyến tính • Lời giải Flamant (bài toán phẳng) P • Độ lún của điểm A so với điểm B: D d P.2(1 − µ o ) D 2 S= ln (3-6) πEo d d s B A • Trong đó: • A, B: 2 điểm đang xét • P: tải trọng tác dụng theo đường thẳng • d: khoảng cách từ điểm đang xét đến điểm lực tác dụng • S: độ lún của nền • Dạng độ lún mặt nền là một đường cong logarit Nguyễn Hồng Nam, 2010 195 Mô hình nền nửa không gian biến dạng tuyến tính Nhận xét: • Mô hình nền bán không gian biến dạng tuyến tính có xét tính phân phối của đất mô hình nền biến dạng tổng quát. • Nhược điểm: Đánh giá thiên lớn tính phân phối của đất, coi chiều sâu nén bằng vô hạn biến dạng mặt nền ra xa vô hạn nên không sát thực nội lực móng lớn • Mô hình này phù hợp với đất nền có tính nén ít và trung bình, chiều dày lớp đất chịu nén khá lớn. Nguyễn Hồng Nam, 2010 196
Mô hình lớp không gian biến dạng tổng thể • Phát triển mô hình bán không gian biến dạng tuyến tính nhưng có xét chiều dày lớp đất chịu nén Ha. • Kết quả tính sát thực hơn. • Nhược điểm: coi Ha là hằng số. thực tế Ha thay đổi theo từng điểm tính lún. Nguyễn Hồng Nam, 2010 197 Tính móng băng theo mô hình nền biến dạng cục bộ 2l b q(x) q(x) p(x) p(x) 4 d W ( x) EJ = q ( x) − p( x) (1) • Phương trình vi phân cơ bản dx 4 d 4 S ( x) EJ + b.c.S ( x) = q( x) (2) dx 4 • Điều kiện tiếp xúc W(x)=S(x) ta có: d 4 S ( x) q ( x) + 4α 4 S ( x) = (3) bc dx 4 EJ Đặt α =4 4EJ Nghiệm (3)=nghiệm tổng quát (4) và 1 nghiệm riêng (3) d 4 S ( x) PTVP thuần nhất khi q(x)=0 4 + 4α 4 S ( x) = 0 (4) Nghiệm của pt(4): dx S ( x) = C1e αx cos αx + C 2 e αx sin αx + C 3 e −αx cos αx + C 4 e −αx sin αx 198 (5) Nguyễn Hồng Nam, 2010
Tính dầm dài vô hạn • Nếu αLtr, αLp>2÷3 coi dầm P dài vô hạn. Lt Lp • X ∞, S(x) 0. x • Nghiệm pt (5) : C1=C2=0. S ( x ) = C3e −αx cos αx + C 4 e −αx sin αx (6) y bc α =4 4EJ Nguyễn Hồng Nam, 2010 199 Tính dầm dài vô hạn khi chịu tác dụng của tải trọng tập trung P P • Bài toán đối xứng qua X=0 (điểm đặt lực P). • Góc xoay:x=0 θ=S’=0 (7) • Lực cắt: x=0 Q=-EJS”’=-P/2. (8) M • Từ (7) C3=C4 P • (8) C3 = C 4 = (9) Q 8α EJ 3 p Các hàm Zimmerman Nguyễn Hồng Nam, 2010 200
Tính dầm dài vô hạn chịu nhiều lực tập trung P tác dụng • Xét dầm dài vô hạn chịu lực tập trung Pi, i=1, n. Cần tính S,p, M,Q tại một điểm bất kỳ. Áp P1 P2 P3 dụng phương pháp đường ảnh hưởng và nguyên lý cộng tác N x dụng. n x1 S = ∑ S io Pi -∞ x2 +∞ x3 x P=1 i =1 Trong đó:n là số lực tác dụng S10 S30 • Sio: tung độ đường ảnh hưởng S20 lún do P=1 đặt tại vị trí điểm tính S(x) toán M gây ra tại vị trí điểm đặt lực tác dụng Pi, cách điểm tính Đường ảnh hưởng lún toán một khoảng xi (khoảng cách từ điểm Pi đến điểm N). • Việc tính toán p, M, Q cũng làm tương tự như tính độ lún S nói 201 Nguyễn Hồng Nam, 2010 trên. Tính toán dầm dài vô hạn chịu mô men tập trung Mo M Q p Mo Mo S= η2 p = α 2 M oη 2 αM o M = η4 4α 2 EJ Q= η1 2 2 Nguyễn Hồng Nam, 2010 202
Tính dầm dài vô hạn chịu tải trọng phân bố b dξ a q(ξ) dp=q(ξ)dξ N 0 x, dξ x ξ d 4 S ( x) q ( x) 4 + 4α 4 S ( x) = dx EJ Để đơn giản, tìm nghiệm ứng với phương trình vi phân thuần nhất đối với dầm chịu tải trọng tập trung -> tính S, M,Q khi dầm chịu tải trọng phân bố. Xét dp=q(ξ)dξ như một lực tập trung --> tính dS,dM,dQ, sau đó lấy tích phân toàn miền phân bố tải trọng. [ ] Xét q=const: q −α ( b− x ) xa: (3-37) S= 2bc e [ q −α ( x −b ) ] cos α ( x − b) − e −α ( x −a ) cos α ( x − a ) [ ] + a
Hệ phương trình vi phân cơ bản p(x) dp=p(xo)dxo A O x Mx B o dxo x, ξ L L d 4 w( x) PTVP trục uốn EJ = q ( x) − p( x) (a) dx 4 2(1 − µo ) 2 B D p(x)~ S(x) S ( x) = πEo A ∫ p( xo ) ln xo − x dxo (b) Điều kiện tiếp xúc w( x) = S ( x) (c) • Một số lời giải: • Gemoskin: Sử dụng gối tựa tính toán thay thế liên kết giữa dầm và nền giải hệ siêu tĩnh • Ximvulidi: p(x) là một hàm parabol bậc 3 205 Nguyễn Hồng Nam, 2010 • Gorbunov-Possadov: lập bảng, sử dụng thuận tiện Phương pháp Gorbunov-Possadov Giả thiết phản lực nền có dạng: p (ξ ) = ao + a1ξ + a2ξ 2 + ... + anξ n (d) ξ = x/L Thay (d) (a) và (b) ta có: EJ d 4 w(ξ ) = q (ξ ) − p (ξ ) (1 − µ 2 ) L4 dξ 4 1−ξ 2(1 − µ o ) L 2 D D là hằng số vì điểm mốc chọn xa s(ξ ) = πEo ∫+ξ ) p(ξ ) ln ρ dρ − (1 dp=p(xo)dxo w(ξ ) = Ao + A1ξ + A2ξ 2 + ... + An ξ n p(x) s (ξ ) = Bo + B1ξ + B2ξ 2 + ... + Bn ξ n x x, ξ A O Mx dxo B xo − x x L L o ρ= , ξo = o = ξ + ρ Nguyễn Hồng Nam, 2010 L L 206
Phương pháp Gorbunov-Possadov • Từ điều kiện tiếp xúc: S(x)=W(x) Ai=Bi • Để tìm p(ξ) bậc n cần (n+1) hệ số ai cần (n+1) phương trình. • Ta có: 2 pt cân bằng tĩnh (lực và mô men) cần (n-1) phương trình. (n-1) pt này lấy từ điểm tiếp xúc. • Gorbunov-Possadov đã lập bảng tính sẵn ứng với nhiều trường hợp móng dầm chịu tải trọng khác nhau. Xem bảng 3-2, 3-3, 3-4, 3-5 Nền và móng, ĐHTL, 1998 • Khi có lực phân bố đều q P • tra bảng (3-3) p, M , Q = f (t , ξ ) x ξ = x / L; α = a / L a • Khi có lực tập trung P hoặc mô men tập trung M O L N x • tra bảng (3-4) hoặc (3-5) L p, M , Q = f (t , ξ , α ) • Nếu móng dầm chịu tác dụng của nhiều tải trọng khác nhau áp dụng nguyên lý cộng tác dụng • Khi lực tác dụng đối xứng p, M, S: đối xứng, Q: phản đối xứng • Nguyễnlực tác dụng phản đối xứng p, M, S: phản đối xứng, Q: đối xứng 207 Khi Hồng Nam, 2010 Các biểu thức tính toán nội lực của dải cứng và ngắn Nội lực Đơn vị Lực phân Lực tập Mô men tập bố q trung P trung M p(ξ) kN/m2 P M p. q p. ± p. L L2 Q(ξ) kN M Q. L.q ± Q. p Q. L M(ξ) kNm M . L2 .q M .P.L ± M.M Nguyễn Hồng Nam, 2010 208