Bài giảng Tinh thể - Khoáng vật - Chương 2: Sự đối xứng của tinh thể

Chia sẻ: Hàn Lâm Cố Mạn | Ngày: | Loại File: PDF | Số trang:25

Thêm vào BST

Báo xấu

14
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Tinh thể - Khoáng vật - Chương 2: Sự đối xứng của tinh thể. Chương này cung cấp cho học viên những nội dung về: các yếu tố đối xứng; phương đơn và phương cân đối; phép cộng các yếu tố đối xứng; các hệ tinh thể;... Mời các bạn cùng tham khảo chi tiết nội dung bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Tinh thể - Khoáng vật - Chương 2: Sự đối xứng của tinh thể

Trường Đại học Bách Khoa TP.HCM Khoa Kỹ thuật Địa chất & Dầu khí Bộ môn Tài nguyên Trái đất và Môi trường Chương 2 SỰ ĐỐI XỨNG CỦA TINH THỂ  Các yếu tố đối xứng  Phương đơn và phương cân đối  Phép cộng các yếu tố đối xứng  Các hệ tinh thể
Các yếu tố đối xứng Tinh thể lặp lại vị trí trong không gian giống ban đầu bằng các phép chiếu, phản chiếu, phép quay hoặc kết hợp đồng thời hai trong ba phép trên. → Tinh thể có tính đối xứng. 2
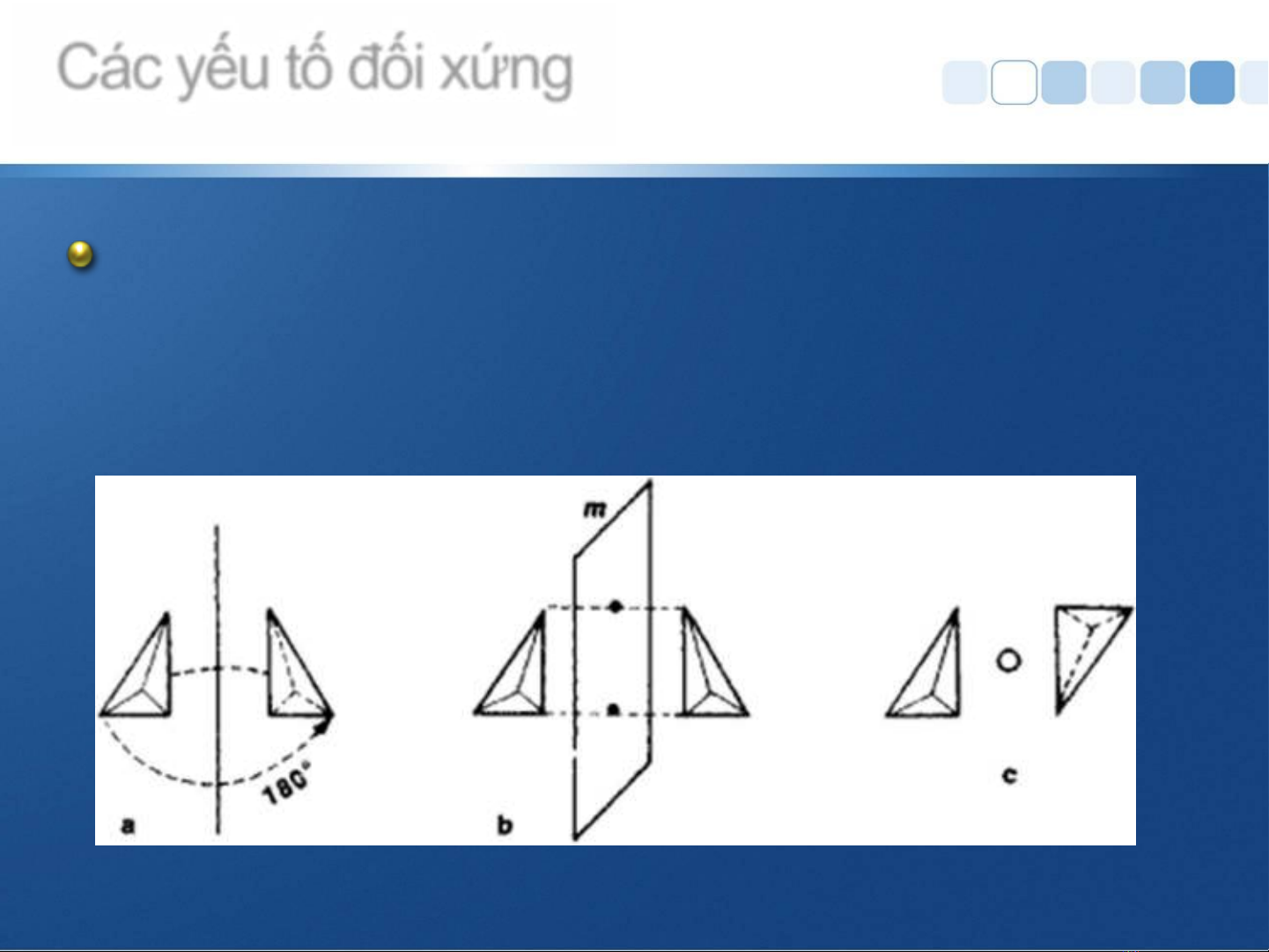
Các yếu tố đối xứng Là một điểm, một đường, một mặt phẳng tưởng tượng mà qua nó hoặc quanh nó hình sẽ trở về vị trí giống như ban đầu. 3
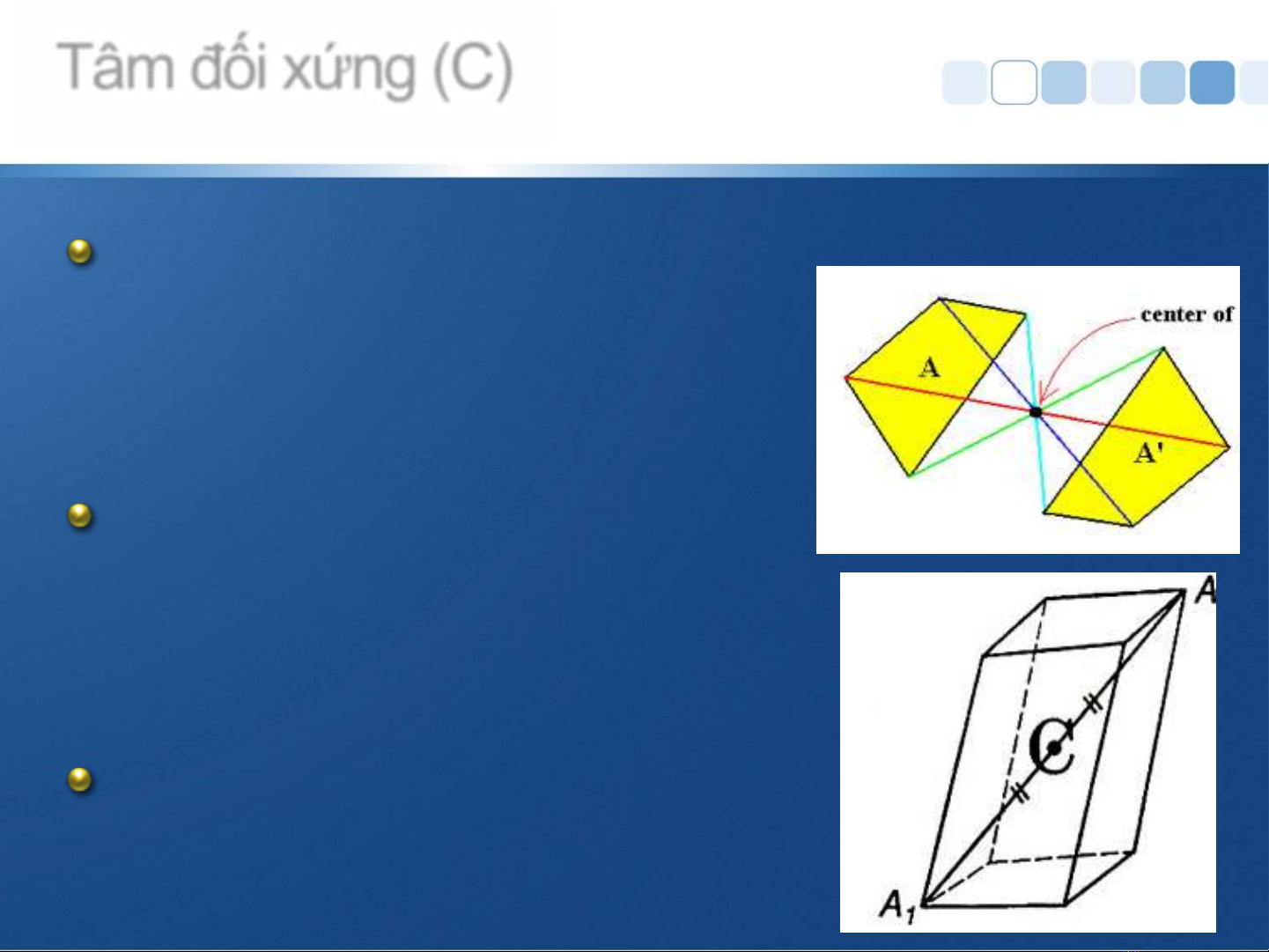
Tâm đối xứng (C) Một điểm bất kỳ → tìm một điểm khác tương ứng và ngược lại → hình có tâm đối xứng. Mọi đường thẳng qua tâm đối xứng đều cắt hình tại hai điểm và nhận tâm đối xứng làm trung điểm. Tâm nghịch đảo. 4
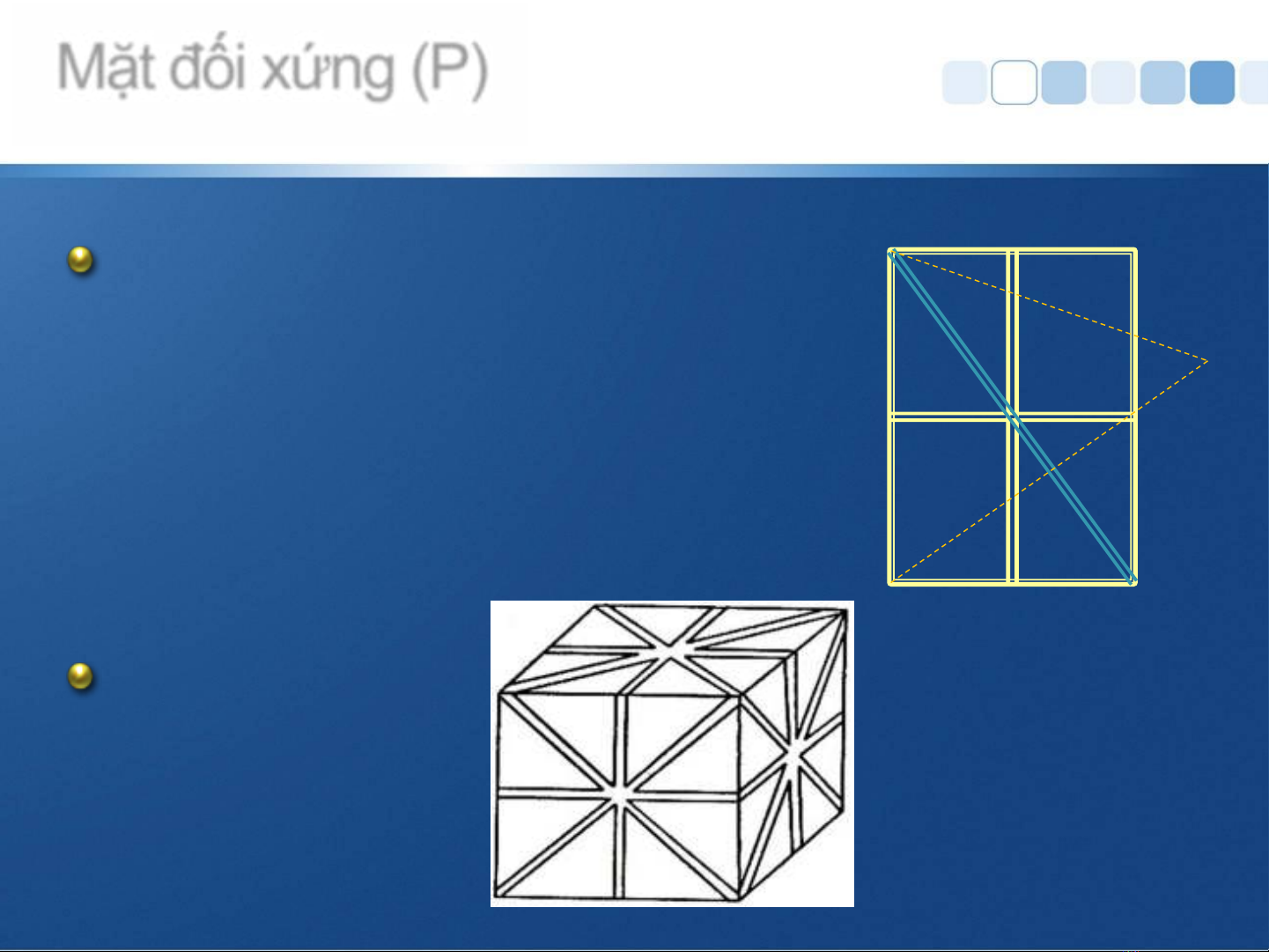
Mặt đối xứng (P) A B Một mặt phẳng chia hình P1 thành hai phần bằng D1 nhau, phần này là ảnh P2 của phần kia qua gương P3 và ngược lại. D C Mặt gương. 5
Trục đối xứng (Ln) Khi quay hình quanh trục với một góc nào đó, hình lặp lại vị trí giống ban đầu. Trục quay. 6
Bậc của trục và góc quay nguyên tố Khi quay hình quanh trục đối xứng 360o → hình lặp lại vị trí giống ban đầu n lần → n là bậc của trục. Góc quay α nhỏ nhất để hình lặp lại vị trí giống ban đầu → α là góc quay nguyên tố (cơ sở). 7
Các định lý về Ln và α Định lý 1: Góc α bao giờ cũng nghiệm đúng đẳng thức: n.α=360o Định lý 2: Không có trục bậc 5 (L5) và trục bậc lớn hơn 6. Nghĩa là n=1; 2; 3; 4; 6. Các vị trí của Ln trong tinh thể? 8
Trục nghịch đảo (Lin) B1 B A A1 C1 Một phương được C thành lập bởi tác dụng E1 đồng thời một trục D E đối xứng và một tâm D1 F F1 A B đối xứng. * Tâm đối xứng không là một yếu tố đối xứng độc lập. D C 9
Trục nghịch đảo (Lin) Li1 Li2 Li3 10
Trục nghịch đảo (Lin) Li4 Li6 11
Ký hiệu các yếu tố đối xứng Yếu tố đối xứng Ký hiệu Hình chiếu nổi Tâm đối xứng. C Mặt đối xứng. P Trục đối xứng bậc 1. L1 Trục đối xứng bậc 2. L2 Trục đối xứng bậc 3. L3 Trục đối xứng bậc 4. L4 Trục đối xứng bậc 6. L6 Trục nghịch đảo bậc 4. Li4 12
Trình tự xác định các yếu tố đối xứng Xác định: Tâm → mặt → trục. Biểu diễn lớp đối xứng: trục → mặt → tâm. 3L44L36L29PC 13
Phương đơn – Phương cân đối Phương đơn (D) Một phương đặc biệt, qua tác dụng của các yếu tố đối xứng, nó không thay đổi vị trí. Phương duy nhất, không lặp lại, không có phương tương ứng (khi thỏa đúng vị trí của D). 14
Phương đơn – Phương cân đối Phương cân đối Phương lặp lại (một số lần) qua tác dụng của các yếu tố đối xứng. L6 L4 L2 15 15
Phương đơn – Phương cân đối Một đa diện chỉ chứa một D. có thể chứa nhiều D. có khi không chứa D nào cả. 16 16
Vị trí của D đối với các yếu tố đối xứng Đối với tâm đối xứng D C: D có thể qua C = Khi có D qua C thì C tác dụng của C không làm thay đổi = phương của D. D1 17
Vị trí của D đối với các yếu tố đối xứng Đối với mặt đối xứng P: D có thể nằm trong P. D có thể vuông góc với P. D không thể xiên góc với P. D D P P D1 P D1 Phép chiếu qua P, Phép chiếu qua P, D không đổi phương Phép chiếu qua P, D không đổi phương LL1 → L’L’1 18 18
Vị trí của D đối với các yếu tố đối xứng Đối với trục đối xứng L: D có thể trùng với trục đối xứng. D có thể vuông góc trục đối xứng bậc 2. D không thể xiên góc với trục đối xứng. DLn L2 Ln D 19 19
Phép cộng các yếu tố đối xứng Định lý: Giao tuyến của hai mặt phẳng đối xứng bao giờ cũng là một trục đối xứng. Tác dụng của trục bằng tổng tác dụng của hai mặt đối xứng và có góc quay nguyên tố bằng hai lần góc giữa hai mặt phẳng đối xứng đó. M1 M2 M1 → M2 → M3 (P1) (P2) (P2) L2 M3 (P1) 20