Bài giảng Xử lý ngôn ngữ tự nhiên (Natural Language Processing): Bài 4 - Lê Thanh Hương

Bài toán PTCP<br /> cây PTCP mẫu<br /> <br /> Phân tích cú pháp<br /> <br /> P<br /> <br /> Lê Thanh Hương<br /> Bộ môn Hệ thống Thông tin<br /> Viện CNTT &TT – Trường ĐHBKHN<br /> Email: huonglt-fit@mail.hut.edu.vn<br /> <br /> T<br /> <br /> tính<br /> <br /> C<br /> <br /> điể<br /> điểm<br /> <br /> câu<br /> <br /> P<br /> cây cú pháp<br /> Văn phạm<br /> <br /> độ chính xác<br /> <br /> Các bộ PTCP<br /> hiện nay có độ<br /> chính xác cao<br /> (Eisner, Collins,<br /> Charniak, etc.)<br /> <br /> 1<br /> <br /> Khái niệm về văn phạm<br /> z<br /> z<br /> z<br /> <br /> Văn phạm<br /> <br /> Phân tích câu “Bò vàng gặm cỏ non”<br /> Cây cú pháp:<br /> Tập luật<br /> z<br /> z<br /> z<br /> z<br /> z<br /> <br /> 2<br /> <br /> z<br /> z<br /> z<br /> <br /> C Æ CN VN<br /> CN Æ DN<br /> VN Æ ĐgN<br /> ĐgN Æ ĐgT DN<br /> DN Æ DT TT<br /> <br /> z<br /> z<br /> z<br /> z<br /> z<br /> <br /> Một văn phạm sản sinh là một hệ thống<br /> G = ( T, N, S, R ), trong đó<br /> T (terminal) – tập ký hiệu kết thúc<br /> N (non terminal) – tập ký hiệu không kết thúc<br /> S (start) – ký hiệu khởi đầu<br /> R (rule) – tập luật<br /> R = { α Æ β | α, β ∈ (T∪N) }<br /> α Æ β gọi là luật sản xuất<br /> <br /> 3<br /> <br /> Nhắc lại về văn phạm<br /> <br /> Dạng chuẩn Chomsky<br /> z<br /> <br /> z<br /> <br /> Mọi NNPNC không chứa ε đều có thể sinh từ<br /> một văn phạm tnđó mọi sản xuất đều có<br /> dạng A Æ BC hoặc A Æ a, với A,B,C∈N và a<br /> ∈T<br /> Ví dụ: Tìm dạng chuẩn Chomsky cho văn<br /> phạm G với T = {a,b}, N ={S,A,B}, R như sau:<br /> z<br /> z<br /> z<br /> <br /> 4<br /> <br /> S Æ bA|aB<br /> A ÆbAA|aS|a<br /> B Æ aBB|bS|b<br /> <br /> z<br /> z<br /> z<br /> z<br /> <br /> Văn phạm: 1 tập luật viết lại<br /> Ký hiệu kết thúc: các ký hiệu không thể phân rã được<br /> nữa.<br /> Ký hiệu không kết thúc: các ký hiệu có thể phân rã<br /> được.<br /> Xét văn<br /> ă phạm<br /> h<br /> G:<br /> G<br /> S → NP VP<br /> NP → John, garbage<br /> VP → laughed, walks<br /> <br /> G có thể sinh ra các câu sau:<br /> John laughed. John walks.<br /> Garbage laughed. 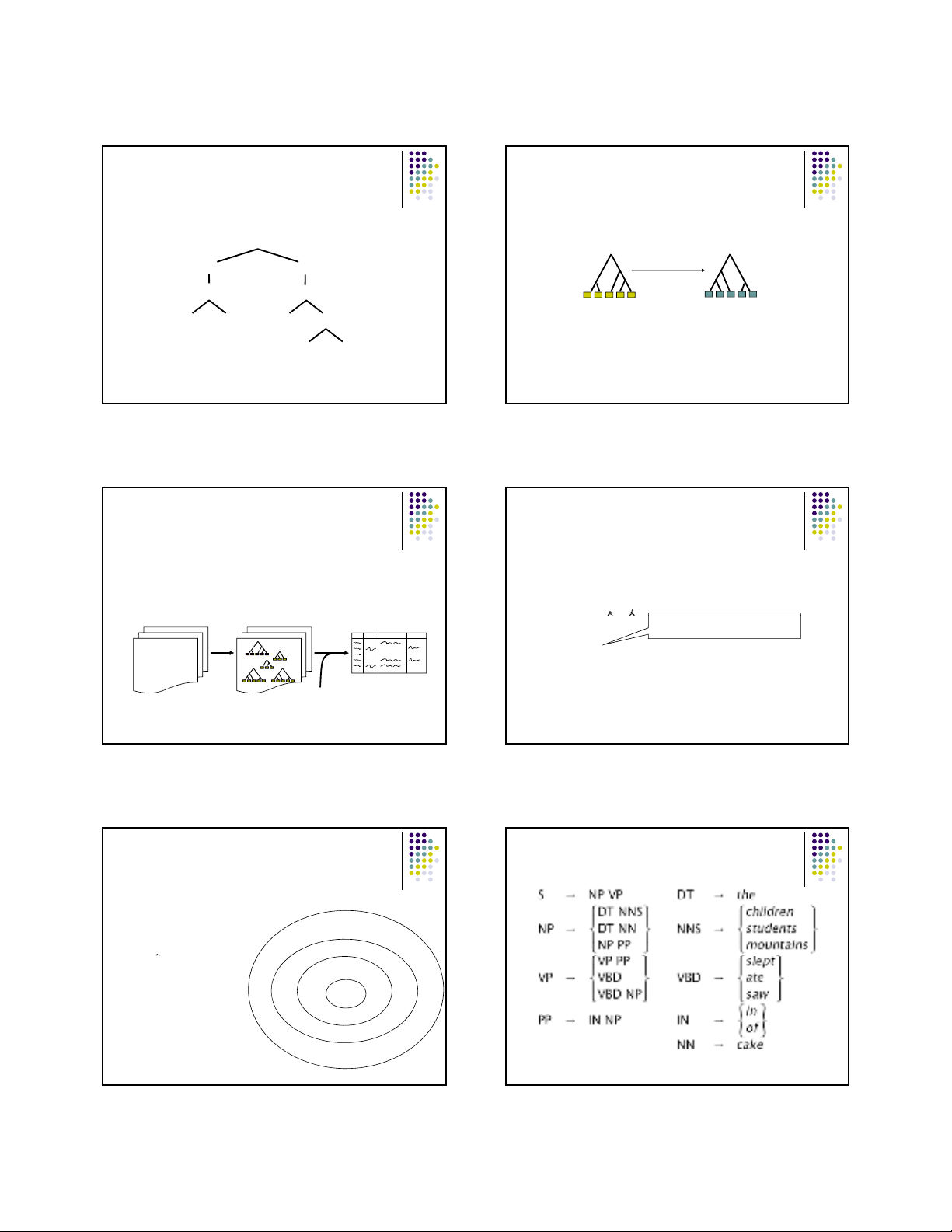Garbage walks.<br /> 5<br /> <br /> 6<br /> <br /> Cấu trúc ngữ pháp<br /> <br /> Các ứng dụng của PTCP<br /> <br /> Cây cú pháp biểu diễn cấu trúc ngữ pháp của một câu.<br /> Bò vàng gặm cỏ non.<br /> <br /> ƒ<br /> <br /> Dịch máy<br /> <br /> (Alshawi 1996, Wu 1997, ...)<br /> <br /> C<br /> <br /> DT<br /> Bò<br /> <br /> CN<br /> <br /> VN<br /> <br /> DN<br /> <br /> ĐgN<br /> ĐgT<br /> gặm<br /> <br /> TT<br /> vàng<br /> <br /> tiếng Anh<br /> <br /> DN<br /> <br /> ƒ<br /> <br /> DT<br /> cỏ<br /> <br /> các thao tác<br /> với cây<br /> <br /> tiếng Việt<br /> <br /> Nhận dạng tiếng nói sử dụng PTCP (Chelba et al 1998)<br /> Put the file in the folder.<br /> Put the file and the folder.<br /> <br /> TT<br /> non<br /> 7<br /> <br /> Văn phạm phi ngữ cảnh<br /> (Context-Free Grammar)<br /> <br /> Các ứng dụng của PTCP<br /> ƒ<br /> <br /> Kiểm tra ngữ pháp<br /> <br /> ƒ<br /> <br /> Trích rút thông tin (Hobbs 1996)<br /> <br /> … còn gọi là văn phạm cấu trúc đoạn<br /> z G = <br /> z T – tập các ký hiệu kết thúc (terminals)<br /> z N - tập các ký hiệu không kết thúc (non-terminals)<br /> z P – ký hiệu tiền kết thúc (preterminals), khi viết lại trở<br /> thành ký hiệu kết thúc,<br /> thúc<br /> P⊂<br /> Nphạm cảm ngữ cảnh<br /> So với<br /> văn<br /> z S – ký hiệu bắt đầu R: αAγ ⇒ αβγ<br /> z R: X → γ , X là ký hiệu không kết thúc; γ là chuỗi các<br /> ký hiệu kết thúc và không kết thúc (có thể rỗng)<br /> z Văn phạm G sinh ra ngôn ngữ L<br /> z Bộ nhận dạng: trả về yes hoặc no<br /> z Bộ PTCP: trả về tập các cây cú pháp<br /> <br /> (Microsoft)<br /> <br /> CSDL<br /> <br /> Kho văn bản<br /> NY Times<br /> <br /> 8<br /> <br /> câu truy vấn<br /> 9<br /> <br /> z<br /> <br /> Văn phạm ngữ cấu:<br /> z<br /> <br /> z<br /> <br /> z<br /> <br /> z<br /> <br /> r = α→β, với α ∈ V+ , β ∈ V* , ⏐α⏐≤⏐β⏐<br /> và α1Aα2→α1β’α2 với β’≠ε<br /> <br /> Văn phạm phi ngữ cảnh:<br /> z<br /> z<br /> <br /> z<br /> <br /> Văn phạm phi ngữ cảnh<br /> <br /> α→β, với α ∈ V+ , β ∈ V*<br /> <br /> Văn phạm cảm ngữ cảnh:<br /> z<br /> <br /> 10<br /> <br /> A → θ, A ∈ N,<br /> với<br /> ới θ ∈ V*=<br /> V* ( T ∪ N )*<br /> <br /> Văn phạm chính qui:<br /> A → aB,<br /> A → Ba,<br /> z A → a,<br /> với A, B ∈ N, a ∈ T.<br /> z<br /> z<br /> <br /> VPCQ<br /> VPPNC<br /> VPCNC<br /> VPNC<br /> 11<br /> <br /> 12<br /> <br /> Cấu trúc đoạn đệ qui<br /> <br /> 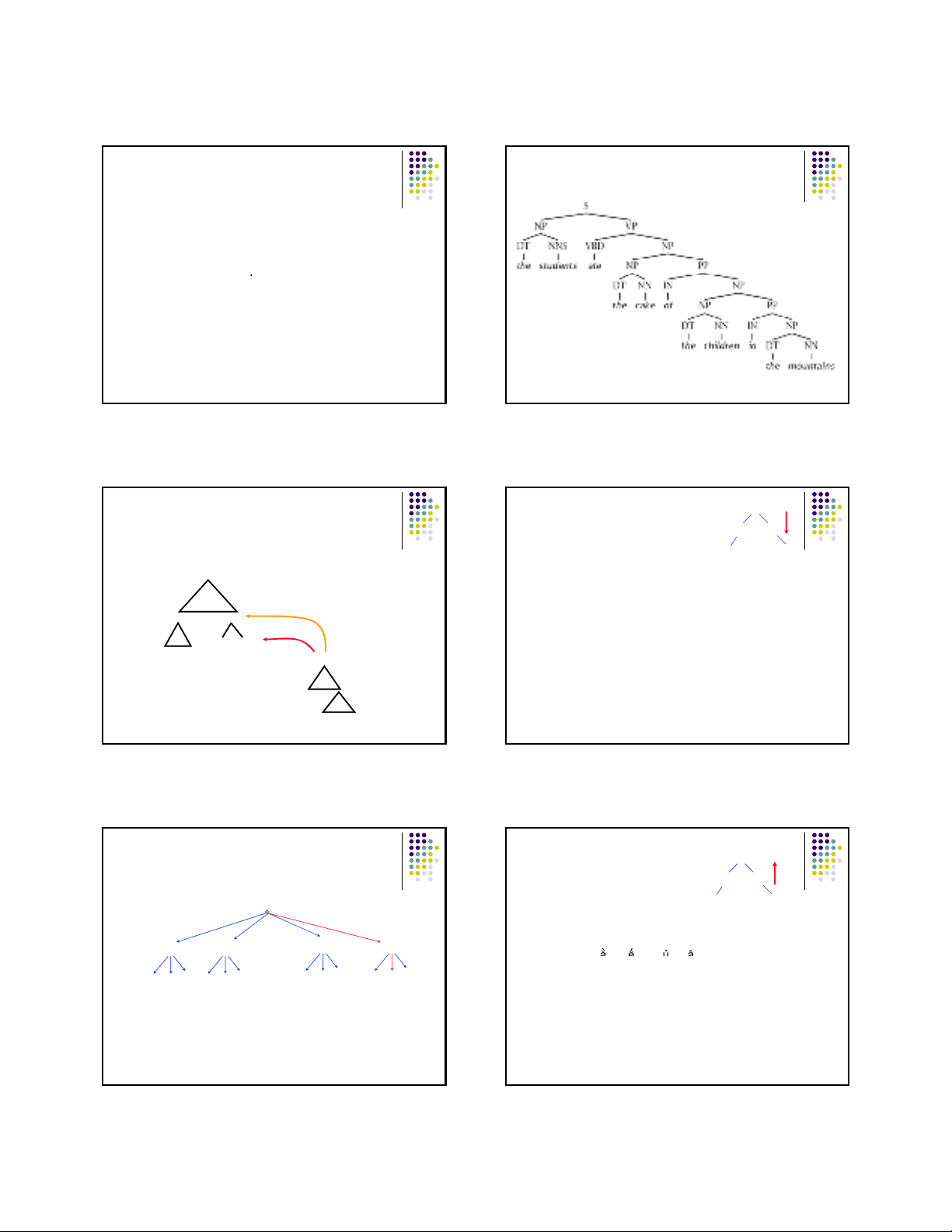Áp dụng tập luật ngữ pháp<br /> z<br /> <br /> S<br /> → NP VP<br /> → DT NNS VBD<br /> → The children slept<br /> p<br /> <br /> z<br /> <br /> S<br /> → NP VP<br /> → DT NNS VBD NP<br /> → DT NNS VBD DT NN<br /> → The children ate the cake<br /> 13<br /> <br /> Văn phạm cho ngôn ngữ tự nhiên<br /> có nhập nhằng<br /> <br /> S<br /> <br /> PTCP kiểu trên xuống<br /> <br /> John saw snow on the campus<br /> S<br /> <br /> NP<br /> 0 John<br /> <br /> 14<br /> <br /> z<br /> <br /> Nhập nhằng - PP<br /> có thể gắn tại 2 điểm (với VP<br /> hoặc với NP)<br /> <br /> z<br /> <br /> z<br /> <br /> VP<br /> <br /> …….<br /> <br /> z<br /> <br /> z<br /> <br /> PP<br /> 3 on<br /> <br /> NP<br /> <br /> z<br /> <br /> VP<br /> <br /> Hướng đích<br /> Khởi đầu với 1 danh sách các ký hiệu cần triển khai (S,<br /> NP,VP,…)<br /> Viết lại các đích trong tập đích bằng cách:<br /> z<br /> <br /> 1 saw NP<br /> 2 snow<br /> <br /> NP<br /> <br /> tìm luật có vế trái trùng với đích cần triển khai<br /> triểu khai nó với vế phải luật, tìm cách khớp với câu đầu vào<br /> <br /> Nếu 1 đích có nhiều cách viết lại Æ chọn 1 luật để áp<br /> dụng (bài toán tìm kiếm)<br /> Có thể sử dụng tìm kiếm rộng (breadth-first search) hoặc<br /> tìm kiếm sâu (depth-first search)<br /> <br /> 4 the 5 campus 6<br /> 15<br /> <br /> Khó khăn với PTCP trên xuống<br /> z<br /> <br /> Các luật đệ qui trái<br /> <br /> z<br /> <br /> PTCP trên xuống rất bất lợi khi có nhiều luật có cùng vế trái<br /> <br /> 16<br /> <br /> PTCP dưới lên<br /> z<br /> <br /> S→NP X2<br /> <br /> ……<br /> <br /> S→NP X600<br /> <br /> VP<br /> …….<br /> <br /> z<br /> <br /> S→NP X1<br /> <br /> S<br /> NP<br /> <br /> z<br /> <br /> S→VP Y1<br /> <br /> z<br /> z<br /> <br /> Nhiều thao tác thừa: triển khai tất cả các nút có thể phân tích trên<br /> xuống<br /> <br /> z<br /> <br /> z<br /> <br /> PTCP trên xuống sẽ làm việc tốt khi có chiến lược điều khiển ngữ<br /> pháp phù hợp<br /> <br /> z<br /> <br /> z<br /> <br /> PTCP trên xuống không thể triển khai các ký hiệu tiền kết thúc<br /> thành các ký hiệu kết thúc. Trên thực tế, người ta thường sử dụng<br /> phương pháp dưới lên để làm việc này.<br /> <br /> z<br /> <br /> Lặp lại công việc: bất cứ chỗ nào có cấu trúc giống nhau<br /> <br /> 17<br /> <br /> Hướng dữ liệu<br /> Khởi tạo với xâu cần phân tích<br /> Nếu chuỗi trong tập đích phù hợp với vế phải của 1 luật<br /> → thay nó bằng vế trái của luật<br /> luật.<br /> Kết thúc khi tập đích = {S}.<br /> Nếu vế phải của các luật khớp với nhiều luật trong tập<br /> đích, cần lựa chọn luật áp dụng (bài toán tìm kiếm)<br /> Có thể sử dụng tìm kiếm rộng (breadth-first search) hoặc<br /> tìm kiếm sâu (depth-first search)<br /> <br /> 18<br /> <br /> Thuật toán CKY (bộ nhận dạng)<br /> <br /> Khó khăn với PTCP dưới lên<br /> z<br /> z<br /> z<br /> <br /> Không hiệu quả khi có nhiều nhập nhằng mức<br /> từ vựng<br /> Lặp lại công việc: bất cứ khi nào có cấu trúc con<br /> chung<br /> Cả PTCP TD (LL) và BU (LR) đều có độ phức<br /> tạp là hàm mũ của độ dài câu.<br /> <br /> ƒ<br /> ƒ<br /> ƒ<br /> <br /> Vào: xâu n từ<br /> Ra: yes/no<br /> Cấu trúc ngữ<br /> g pháp:<br /> p p bảng<br /> g n x n ((chart table))<br /> ƒ<br /> ƒ<br /> ƒ<br /> <br /> hàng đánh số 0 đến n-1<br /> cột đánh số 1 đến n<br /> cell [i,j] liệt kê tất cả các nhãn cú pháp giữa i và j<br /> <br /> 19<br /> <br /> Thuật toán CKY (bottom-up)<br /> ƒ<br /> <br /> ƒ<br /> <br /> 20<br /> <br /> Ví dụ<br /> <br /> for i := 1 to n<br /> ƒ Thêm tất cả từ loại của từ thứ i vào ô [i-1,i]<br /> for width := 2 to n<br /> ƒ for start := 0 to n-width<br /> ƒ end := start + width<br /> ƒ for mid := start+1 to end-1<br /> ƒ for mọi nhãn cú pháp X trong [start,mid]<br /> ƒ<br /> for mọi nhãn cú pháp Y trong [mid,end]<br /> ƒ<br /> for mọi cách kết hợp X và Y (nếu có)<br /> ƒ<br /> Thêm nhãn kết quả vào [start,end] nếu chưa<br /> <br /> Bò<br /> <br /> vàng<br /> <br /> gặm<br /> <br /> 2<br /> <br /> 3<br /> <br /> 1<br /> 0<br /> DT<br /> <br /> 3.<br /> 4.<br /> 5.<br /> 6.<br /> 7.<br /> 8.<br /> <br /> 5<br /> C<br /> <br /> TT<br /> 2<br /> <br /> VN<br /> ĐgN<br /> <br /> ĐgT<br /> 3<br /> DT<br /> <br /> DN<br /> <br /> 4<br /> TT<br /> <br /> Văn phạm phi ngữ cảnh<br /> Start→ S<br /> S → NP VP<br /> NP → Det Noun<br /> NP → Name<br /> NP → Name PP<br /> PP → Prep NP<br /> VP → V NP<br /> VP → V NP PP<br /> <br /> 4<br /> <br /> CN<br /> DN<br /> <br /> 21<br /> <br /> 2.<br /> <br /> non<br /> <br /> 1<br /> <br /> có nhãn này<br /> <br /> 1.<br /> <br /> cỏ<br /> <br /> 9.<br /> 10.<br /> 11.<br /> 12.<br /> 13.<br /> 14.<br /> 15.<br /> <br /> 22<br /> <br /> Luật kết hợp<br /> <br /> V → ate<br /> Name → John<br /> Name → ice-cream, snow<br /> Noun → ice-cream, pizza<br /> Noun → table, guy, campus<br /> Det → the<br /> Prep → on<br /> <br /> Ô Cell[i,j] chứa nhãn X nếu<br /> <br /> z<br /> z<br /> z<br /> <br /> z<br /> <br /> 23<br /> <br /> Có luật X→YZ;<br /> Cell[i,k] chứa nhãn Y và ô Cell[k,j] chứa nhãn Z,<br /> với k nằm<br /> ằ giữa i và j;<br /> <br /> VD: NP → DT [0,1] NN[1,2]<br /> <br /> 24<br /> <br /> CKY phải sử dụng luật nhị<br /> phân<br /> <br /> CKY chart<br /> “ The<br /> <br /> guy ate the ice-cream on<br /> <br /> 1<br /> z<br /> <br /> Chuyển VP→V NP PP thành:<br /> <br /> 0<br /> 1<br /> 2<br /> 3<br /> 4<br /> 5<br /> 6<br /> 7<br /> <br /> 8.a. VP→V Arguments<br /> 8 b Arguments → NP PP<br /> 8.b.<br /> <br /> 2<br /> <br /> 3<br /> <br /> 4<br /> <br /> 5<br /> <br /> the table”<br /> <br /> 6<br /> <br /> 7<br /> <br /> 8<br /> <br /> DT<br /> NN<br /> VBD<br /> <br /> DT<br /> NN<br /> IN<br /> DT<br /> NN<br /> <br /> 25<br /> <br /> 26<br /> <br /> Nhập nhằng!<br /> <br /> Áp dụng thao tác ‘dán’<br /> 1<br /> 0<br /> 1<br /> 2<br /> 3<br /> 4<br /> 5<br /> 6<br /> 7<br /> <br /> 2<br /> <br /> 3<br /> <br /> 4<br /> <br /> 5<br /> <br /> 6<br /> <br /> 7<br /> <br /> 1<br /> <br /> 8<br /> <br /> 0<br /> 1<br /> 2<br /> 3<br /> <br /> DT NP<br /> NN<br /> VBD<br /> DT<br /> NN<br /> IN<br /> DT<br /> NN<br /> 27<br /> <br /> Thuật toán Earley (top-down)<br /> z<br /> <br /> B<br /> <br /> C<br /> <br /> +<br /> D<br /> <br /> D<br /> <br /> E<br /> <br /> A→BC.DE<br /> <br /> B<br /> <br /> C<br /> <br /> D<br /> <br /> E<br /> <br /> Tiến hành dần từ trái sang phải<br /> <br /> 5<br /> <br /> 6<br /> <br /> 7<br /> <br /> 8<br /> S<br /> <br /> VBD<br /> <br /> VP<br /> NP,<br /> Args<br /> <br /> DT NP<br /> <br /> 4<br /> 5<br /> 6<br /> 7<br /> <br /> NN<br /> IN<br /> DT<br /> <br /> PP<br /> NP<br /> NN<br /> <br /> 28<br /> <br /> NP → Papa<br /> N → caviar<br /> N → spoon<br /> V → ate<br /> P → with<br /> Det<br /> → the<br /> Det<br /> →a<br /> <br /> A→BCD.E<br /> 29<br /> <br /> z<br /> <br /> 4<br /> <br /> DT NP<br /> NN<br /> <br /> ROOT → S<br /> S<br /> → NP VP<br /> NP → Det N<br /> NP → NP PP<br /> VP<br /> → VP PP<br /> VP<br /> → V NP<br /> PP<br /> → P NP<br /> <br /> A<br /> <br /> =<br /> <br /> 3<br /> <br /> Ví dụ<br /> <br /> Tìm các nhãn và các nhãn thiếu (partial constituents) từ<br /> đầu vào<br /> z A → B C . D E là nhãn thiếu:<br /> <br /> A<br /> <br /> 2<br /> <br /> 5. NP → NN PP<br /> 8.a. VP→V Arguments<br /> 8.b. Arguments → NP PP<br /> <br /> 30<br /> <br />