1
BÀI TẬP DÀI MÔN ĐIỀU KHIỂN TỰ ĐỘNG
PHẦN I/ YÊU CẦU THIẾT KẾ
1) Yêu cầu thiết kế hệ thống điềukhiển tự động có:
- Bộ điều khiển PID có hàm truyền :
WPID(s) = KP*(1+ sTI*
1+TD*s)
- Đối tượng điều khiển là khâu trễ và quán tính bậc nhất có hàm truyền:
WDT(s) = 1* +
−
sT
eLs
Với các tham số: L/T = 0.9; T = 95;
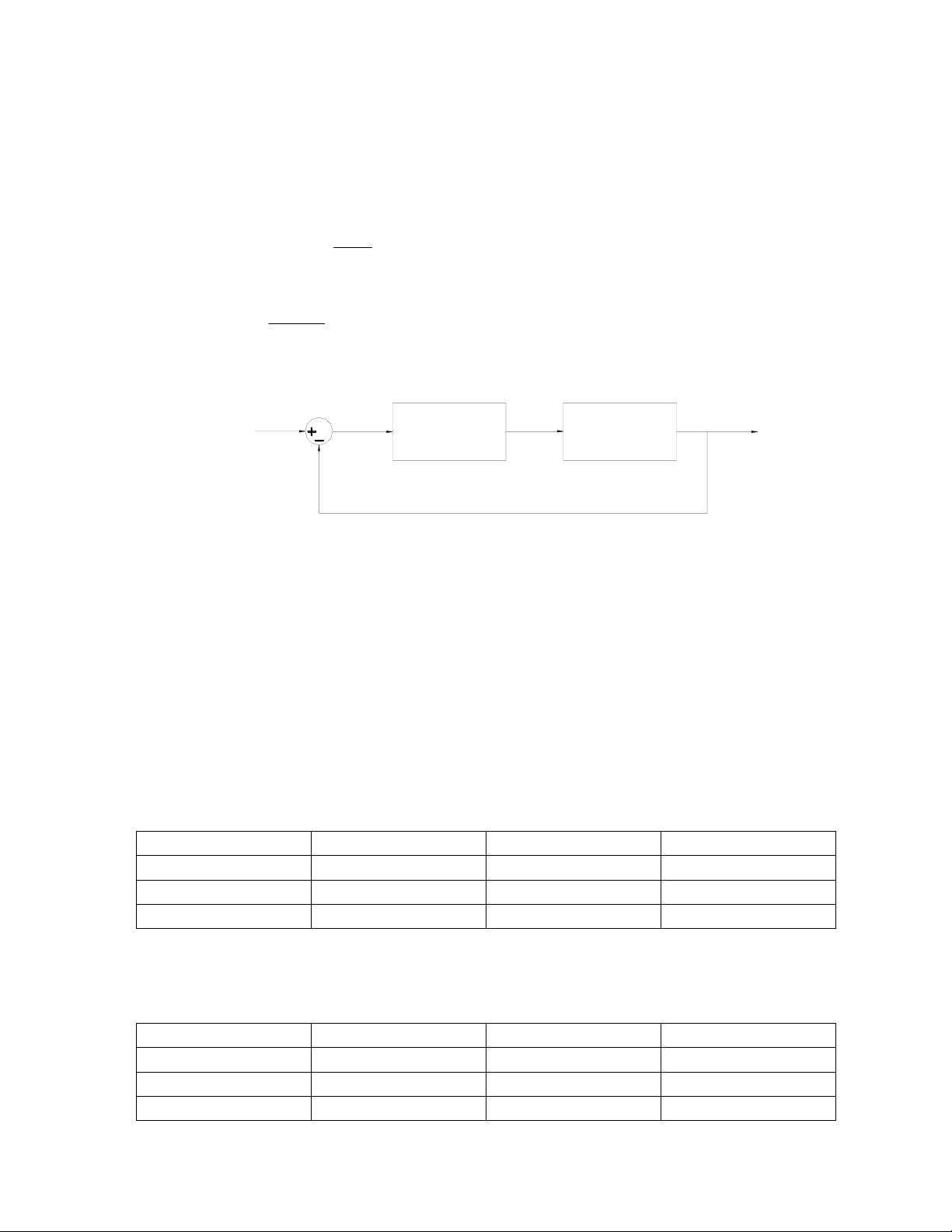
Hệ thống có sơ đồ như hình vẽ:
Wpid(s)Wdt(s)
2) Tính toán các tham số Kp, Ti, Td đảm bảo tính ổn định và chất lượng của
hệ thống (theo Ziegler – Nichols).
3) Xét ổn định của hệ thống. Tìm các điểm cực và điểm không.
4) Khảo sát chất lượng, chọn các tham số với các luật điều khiển P, PI, PID
đảm bảo cho hệ thống có chất lượng tốt nhất (chỉnh định bằng tay).
5) Tính tham số tối ưu của bộ điều khiển PID dùng hàm least – squares (sai số
bình phương nhỏ nhất) với các tham số L và T đã cho ở trên.
PHẦN II/ TÍNH TOÁN VỚI MATLAB
I/ Tính toán các tham số Kp, Ti, Td theo tiêu chuẩn Ziegler – Nichols
Áp dụng bảng công thức thực nghiệm của Ziegler – Nichols:
Luật điều khiển Kp Ti Td
P T/L
∞
0
PI 0.9T/L 10L/3 0
PID 1.2T/L 2L 0.5L
Với các tham số đã cho: L/T = 0.9; T = 95 ⇒L=85.5
Thay vào bảng trên ta có:
Luật điều khiển Kp Ti Td
P 1.111
∞
0
PI 1 285 0
PID 1.333 171 42.75
2
II/ Phân tích hệ thống với các tham số chọn theo phương pháp Ziegler –
Nichols và hiệu chỉnh bằng tay
Để có thể phân tích hệ thống, ta cần khai triển Taylor khâu trễ e-Ls, lấy 3 số
hạng đầu là đủ chính xác. Việc khai triển này đựơc thực hiện nhờ MatLab qua hàm
xấp xỉ Pade:
Chương trình MatLab như sau:
>> [ts,ms]=pade(85.5,3)
ts =
-1.0000 0.1404 -0.0082 0.0002
ms =
1.0000 0.1404 0.0082 0.0002
>> wtre=tf(ts,ms)
Transfer function:
-s^3 + 0.1404 s^2 - 0.008208 s + 0.000192
---------------------------------------------------
s^3 + 0.1404 s^2 + 0.008208 s + 0.000192
1/ Khảo sát hệ thống với luật điều khiển tỉ lệ P:
>> T=95;L=85.5;
>> [ts,ms]=pade(L,3)
ts =
-1.0000 0.1404 -0.0082 0.0002
ms =
1.0000 0.1404 0.0082 0.0002
>> wdt=tf(ts,ms)*tf(1,[T 1])
Transfer function:
-s^3 + 0.1404 s^2 - 0.008208 s + 0.000192
------------------------------------------------------
95 s^4 + 14.33 s^3 + 0.9201 s^2 + 0.02645 s + 0.000192
>> Kp=T/L
Kp =
1.1111
>> wkinp=feedback(Kp*wdt,1)
Transfer function:
-1.111 s^3 + 0.1559 s^2 - 0.00912 s + 0.0002133
------------------------------------------------------
95 s^4 + 13.22 s^3 + 1.076 s^2 + 0.01733 s + 0.0004053
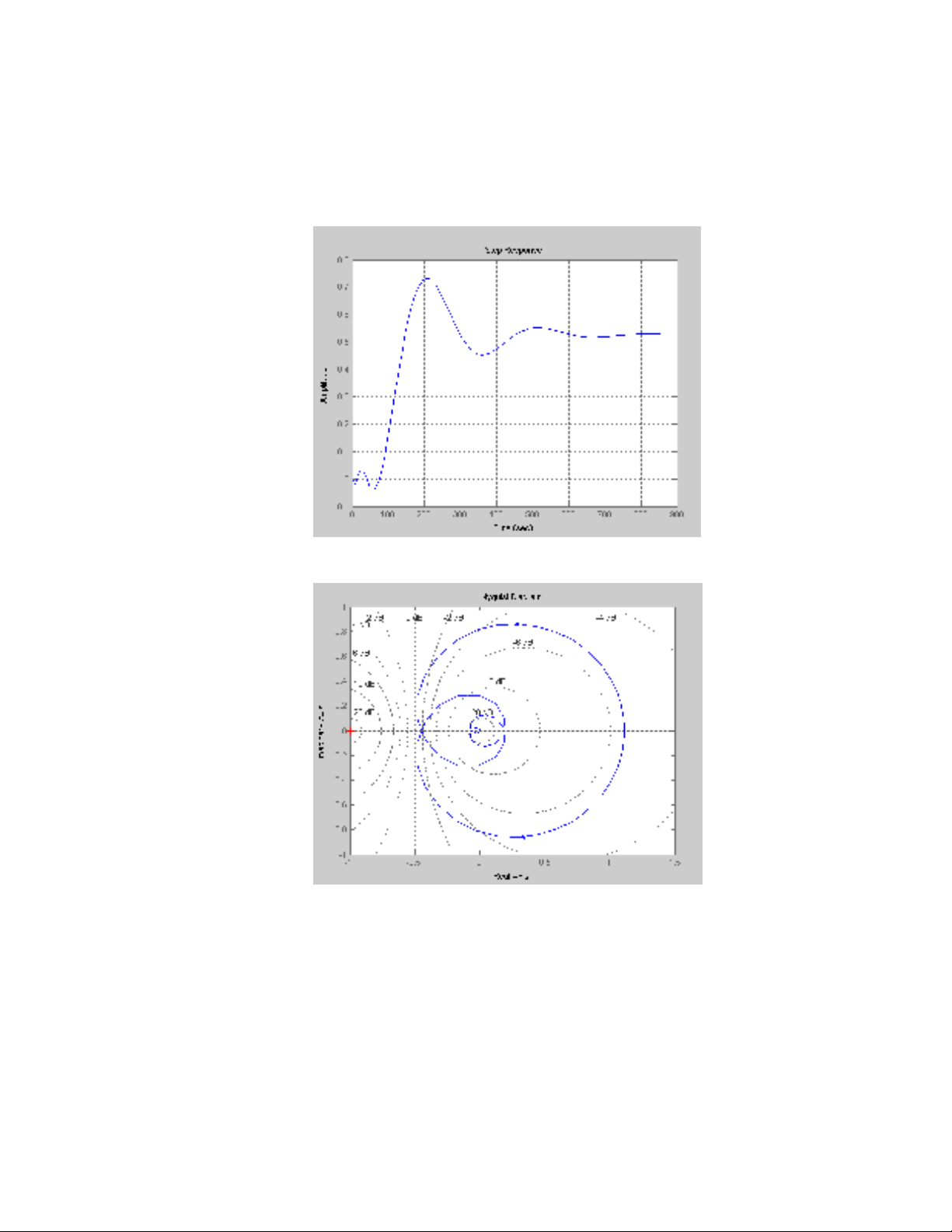
>> step(wkinp)
>> nyquist(wkinp)
>> pzmap(wkinp)
>> [p,z]=pzmap(wkinp)
p =
-0.0628 + 0.0722i
-0.0628 - 0.0722i
-0.0068 + 0.0205i
3
-0.0068 - 0.0205i
z =
0.0430 + 0.0410i
0.0430 - 0.0410i
0.0543
Đặc tính quá độ
Đặc tính tần số
4
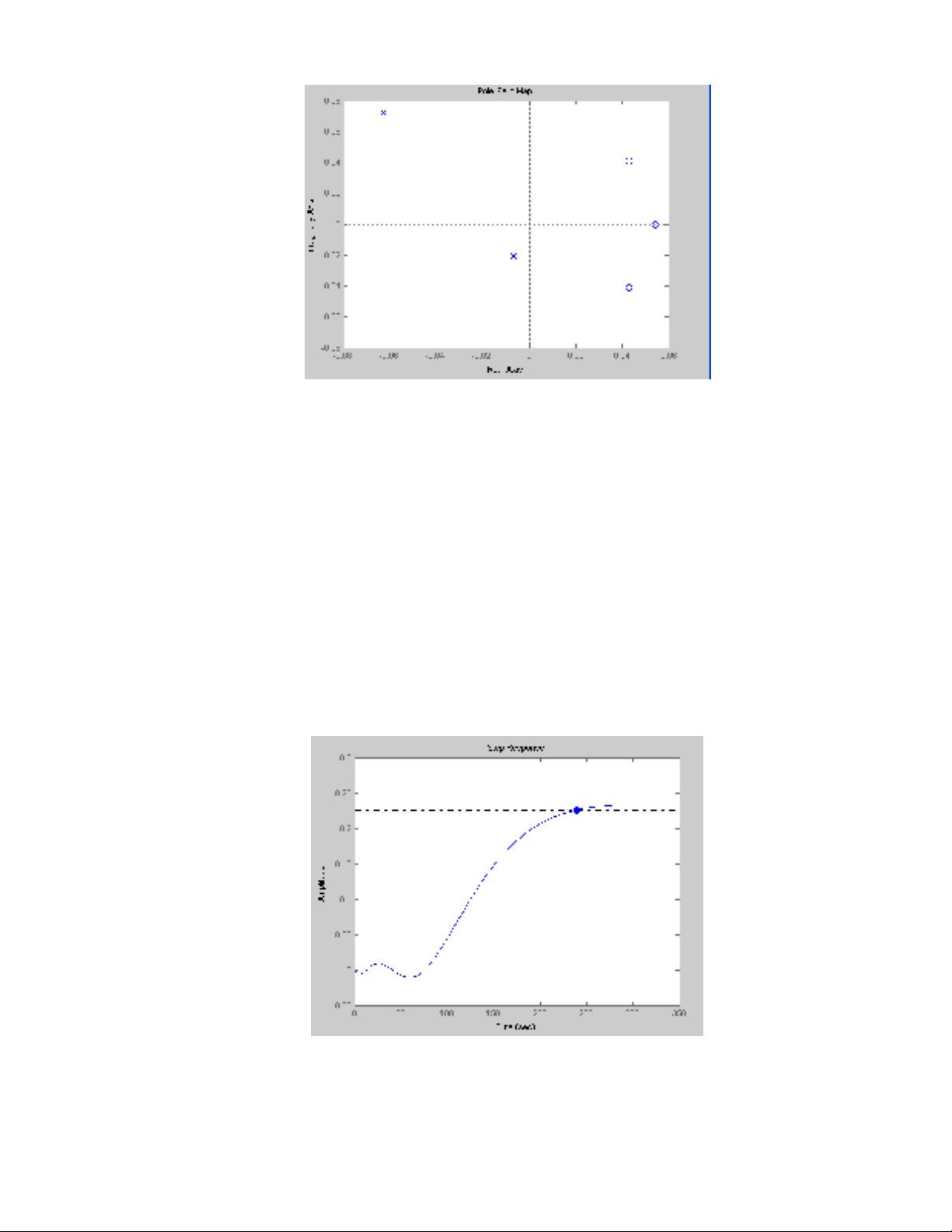
Đồ thị điểm không, điểm cực
*Nhận xét:
- Các điểm cực đều nằm bên trái trục ảo nên hệ thống ổn định.
- Độ quá điển khiển max
δ
= 39%
- Thời gian tăng tốc (Rise time): 54.1s
- Thời gian quá độ (Settling time): 573s.
*Hiệu chỉnh để có đặc tính quá độ tốt hơn: cho Kp = 0.3
>> Kp = 0.3;
>> wkinp = feedback(Kp*wdt,1)
Transfer function:
-0.3 s^3 + 0.04211 s^2 - 0.002462 s + 5.76e-005
-------------------------------------------------------
95 s^4 + 14.03 s^3 + 0.9622 s^2 + 0.02398 s + 0.0002496
>> step(wkinp)
- Sau khi hiệu chỉnh có:
+ Độ quá điều chỉnh max
δ
= 1.24%
+ Thời gian quá độ: 239 (s)
5
+ Thời gian tăng tốc: 112 (s)
2/ Khảo sát hệ thống với luật điều chỉnh tỉ lệ – tích phân PI
Chương trình Matlab:
>> T=95; L=85.5
>> Kp=0.9*T/L;Ti=10*L/3;
>> [ts,ms]=pade(L,3)
ts =
-1.0000 0.1404 -0.0082 0.0002
ms =
1.0000 0.1404 0.0082 0.0002
>> wdt=tf(ts,ms)*tf(1,[T 1])
Transfer function:
-s^3 + 0.1404 s^2 - 0.008208 s + 0.000192
------------------------------------------------------
95 s^4 + 14.33 s^3 + 0.9201 s^2 + 0.02645 s + 0.000192
>> wpi=tf([Kp*Ti Kp],[Ti 0])
Transfer function:
285 s + 1
---------
285 s
>> wkinpi=feedback(wdt*wpi,1)
Transfer function:
-285 s^4 + 39 s^3 - 2.199 s^2 + 0.04651 s + 0.000192
------------------------------------------------------------------
27075 s^5 + 3800 s^4 + 301.2 s^3 + 5.339 s^2 + 0.1012 s + 0.000192
>> step(wkinpi)
>> nyquist(wdt*wpi)
>> pzmap(wkinpi)
>> [p,z]=pzmap(wkinpi)
p =
-0.0618 + 0.0694i
-0.0618 - 0.0694i
-0.0073 + 0.0184i
-0.0073 - 0.0184i
-0.0021
z =
0.0430 + 0.0410i
0.0430 - 0.0410i
0.0543
-0.0035