e
I
>
H
b
ị
Tr
o
W
ch
ỉ
T
ừ
Xác
đ
Xác
đ
của
h
Xác
đ
B
>
Xác địn
h
H
àm truyề
n
ị
.
Ta có
h
W
=
o
ng đó :
W
W
g
(p) là hà
m
ỉ
nh
ừ
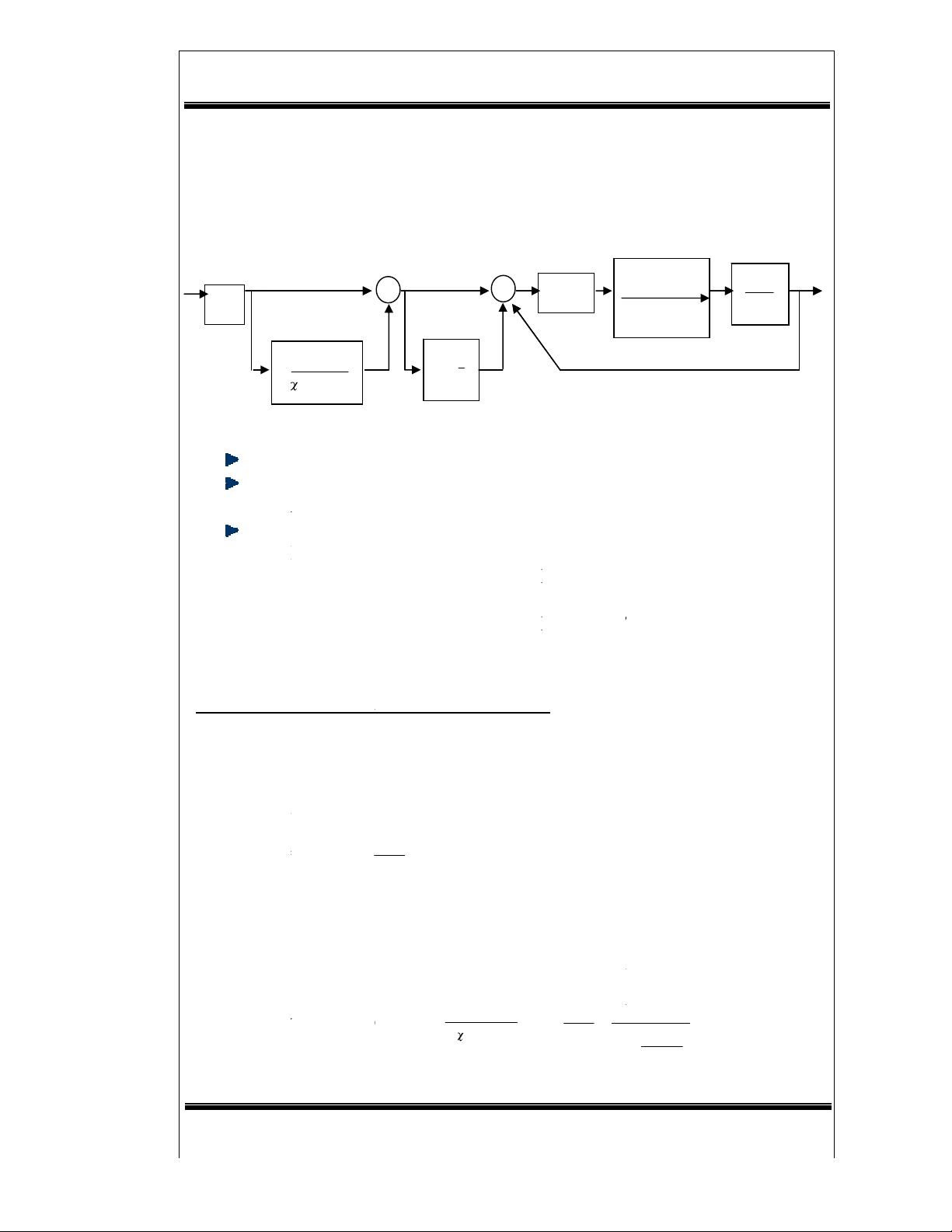
sơ đồ su
y
α
K
B
à
THI
Ế
đ
ịnh hàm t
r
đ
ịnh mối l
i
h
ệ thống.
đ
ịnh các t
h
B
iết:
Th
ô
Th
ô
Các
h
hàm tr
u
n
đạt là hà
m
h
àm truyề
n
W
m
(p) =
W
=
K
m
( 1+
W
q
(p) là hà
m
m
gánh : l
à
y
ra : W
m
(
p
1T
2
2
+p
pT
α
à
i tập dài
m
B
À
Ế
T BỊ
Đ
r
uyền đạt
c
i
ên hệ giữ
a
h
ông số củ
a
ô
ng số của
ô
ng số của
thông số
k
uy
ền đạt c
ủ
m
mô tả
m
n
đạt của t
h
W
q
(p) . W
g
(
pTi.
1
+ T
d
p)
m
truyền
đ
à
thành p
h
p
) =K(1+
(
α
p
T
1
1
m
ôn Thiết
b
1
À
I TẬP
Đ
IỀU C
H
c
ủa thiết b
ị
a
các thôn
g
a
thiết bị t
r
hệ thống:
K
Rơle:
b
k
hác:
K
ủ
a thiết b
ị
m
ối quan
h
h
iết bị có
d
(
p)
)
. W
g
(p)
α
đ
ạt của qu
y
h
ần kí sin
h
1p.T
.pT
2
2
+
α
)(1
p
b
ị ĐCTĐ
C
DÀI
H
ỈNH
T
-
ị
g
số của th
i
r
ong các c
h
K
m
=2
T
b
=1
K
1
=25
T
ị
:
h
ệ giữa đầ
u
d
ạng như
s
α
y
luật điều
h
trong lò
n
+
pT1
1
).
K
1
K
1
C
N I
T
ĐCN
I
i
ết bị với
c
h
ế độ P, P
I
T
i
=72
T
mb=0.5
T
c=20c
u
vào và đ
s
au :
chỉnh
n
g cấu trúc
pT
KK
pTK
K
c
r
cr
1
1
/
+
I
c
ác thông
s
I
, PD, PID
.
T
d
=15
c=18
α=0.1
ầu ra của
t
của máy
pT
c
1
u
s
ố
.
t
hiết
điều

Bài tập dài môn Thiết bị ĐCTĐCN I
2
=K(1+ 1
2
2
+pT
pT
α
)(1+ pT1
1). KrKTcp
KrK
1
1
+
=K[(1+α)T2p+1](1+ pT1
1) .
)12)(1
1
(
1
++ pTp
Kr
K
Tc
α
Từ đó suy ra:
¾ Quy luật điều chỉnh:
Wq(p)= K[(1+α)T2p+1](1+ pT1
1)
=K[(1+α)T2p+(1+α)
1
2
T
T+1+ pT1
1]
=K.
1
21 )(1
T
TT
α
++ [1+ pTT
p
TT
TT 1
.
)1(
1
)(1
)(1
2121
21
αα
α
++
+
++
+]
Đặt:
21
21
)1(
)1(
TT
TT
α
α
++
+ =Td : Hằng số thời gian vi phân.
T
1+(1+α)T2 =Ti : Hằng số thời gian tích phân.
K.
1
21 ))(1
T
TT
α
++ =Km : Hệ số khuếch đại.
Từ đó ta có hàm truyền của quy luật điều chỉnh như sau:
Wq(p)= Km ( 1+ pTi.
1+ Tdp)
¾ Hàm gánh:
Wg(p)=
)1)(1(
1
2
1
++ pTp
KK
T
r
c
α
Từ đó suy ra:
Ag(w)=
]1)].[(1)[(
1
2
2
2
1
++ wTw
KK
T
r
c
α
φg(w)=-[arctg
r
c
KK
wT
1
+ arctg(αT2w)]

Bài tập dài môn Thiết bị ĐCTĐCN I
3
Ö Vùng làm việc bình thường của máy điều chỉnh là:
⎪
⎪
⎩
⎪
⎪
⎨
⎧≤
++
−A
wTw
KrK
Tc
δ
α
]1)2].[(1)
1
[(
1
1
22
≤ T2w)arctg( +
K1K
r
Tcw
arctg
α
Δφ
II> Xác định mối liên hệ giữa các thông số của thiết bị và các thông số của
hệ thống.
¾ Các thông số của hệ thống là: Km, Ti,Td.
¾ Các thông số của thiết bị là: K, T1, T2.
Xác định mối liên hệ giữa các thông số của thiết bị và thông số của
hệ thống:
Ta có:
K
1
21 ))(1
T
TT
α
++ =Km
T
i =T1+(1+α)T2
Td = 2)1(1
21)1(
TT
TT
α
α
++
+=Ti
TT 21)1(
α
+
=>TiTd=(1+α)T1T2
Đặt d= Ti
Td => Ta có: Ti=T1+(1+α)T2
dT
i
2=(1+α)T1T2
Giải hệ phương trình trên với điều kiện T1>T2 ta có:
T
1=2
)411( dTi −+
T
2=)1(2
)411(
α
+
−− dTi
III> Xác định các thông số của thiết bị trong các chế độ P, PI, PD, PID.
Ta có hàm truyền đạt của quy luật điều chỉnh:
W
q(p)= Km ( 1+ pTi.
1+ Tdp)
¾ Chế độ P:
Cho: ⎩
⎨
⎧
∞=
=
d
T
T0
1 ⇒⎩
⎨
⎧
=
∞=
0
2
1
T
T hoặc ⎩
⎨
⎧
∞=
=
2
10
T
T

Bài tập dài môn Thiết bị ĐCTĐCN I
4
nhưng vì: K
1
21 ))(1
T
TT
α
++ =Km nên 0
1
≠
T
Vì vậy chỉ còn trường hợp ⎩
⎨
⎧
=
∞=
0
2
1
T
T
Ta có: K
1
21 ))(1
T
TT
α
++ =Km
21
1
)1( TT
TK
Km
α
++
=⇒
Ta cho
1
T một giá trị vô cùng lớn để tính giá trị của K.
Giả sử cho 000.10
1=T 2
0)1,01(100000
1000002 ==
×++
×
=⇒ m
KK
¾ Chế độ PI:
Ở chế độ này thì ta cho 0
=
d
T
Theo bài ra ta có: 72
=
i
T
Mà: Ti =T1+(1+α)T2
Td = 2)1(1
21)1(
TT
TT
α
α
++
+=Ti
TT 21)1(
α
+
Suy ra: 0
72
2
1
=
=
=
T
TT i 72
)1( 21
1==
++
=⇒ m
mK
TT
TK
K
α
¾ Chế độ PD:
Ở chê độ này ta có:
=
i
T
∞
và d=0
Theo bài ra ta có: 15
=
d
T
Mà: Ti =T1+(1+α)T2
Td = 2)1(1
21)1(
TT
TT
α
α
++
+=Ti
TT 21)1(
α
+
và: T1=2
)411( dTi −+
T2=)1(2
)411(
α
+
−− dTi
Suy ra: 15
2
1
==
∞
=
=
d
i
TT
TT
Cho Ti một giá trị thật lớn VD: Ti=100 000
⇒ 15
100000
2
1
=
=
T
T
=⇒ K1.9967

Bài tập dài môn Thiết bị ĐCTĐCN I
5
¾ Chế độ PID:
Ta có các thông số như sau:
15
72
2
=
=
=
d
i
m
T
T
K
208.0
72
15 ===⇒
i
d
T
T
d
Từ đó ta tính được các thông số của hệ thống như sau:
41.1
3.19
75.50
2
1
=
=
=
K
T
T
IV>Xây dựng hàm quá độ trong các chế độ P, PI, PD, PID.
Để xây dựng được hàm quá độ trong các chế độ trên ta đi xây dựng mô
hình hệ thống chung cho hệ thống rồi thay các thông số của hệ thống trong
từng trường hợp riêng vào. Cho đầu vào là xung step rồi dùng Scope đo tín
hiệu đầu ra ta sẽ có được dạng hàm quá độ trong từng trường hợp.
Vì trong thư viện của Simulink không có khâu Rơle 3 vị trí có trễ nên
ta phải ghép hai khâu Rơle 2 vị trí có trễ lại để được khâu Rơle 3 vị trí có trễ
1.Chế độ P:
Các thông số như tính toán ở trên:
2
0
10000
2
1
=
=
=
K
T
T
Kết quả đo tín hiệu đầu ra:


























