U
C
0
U
R
0
U
M N
U
A M
N
A
B
U
A B
M
i
C¸c vÝ dô minh ho¹:
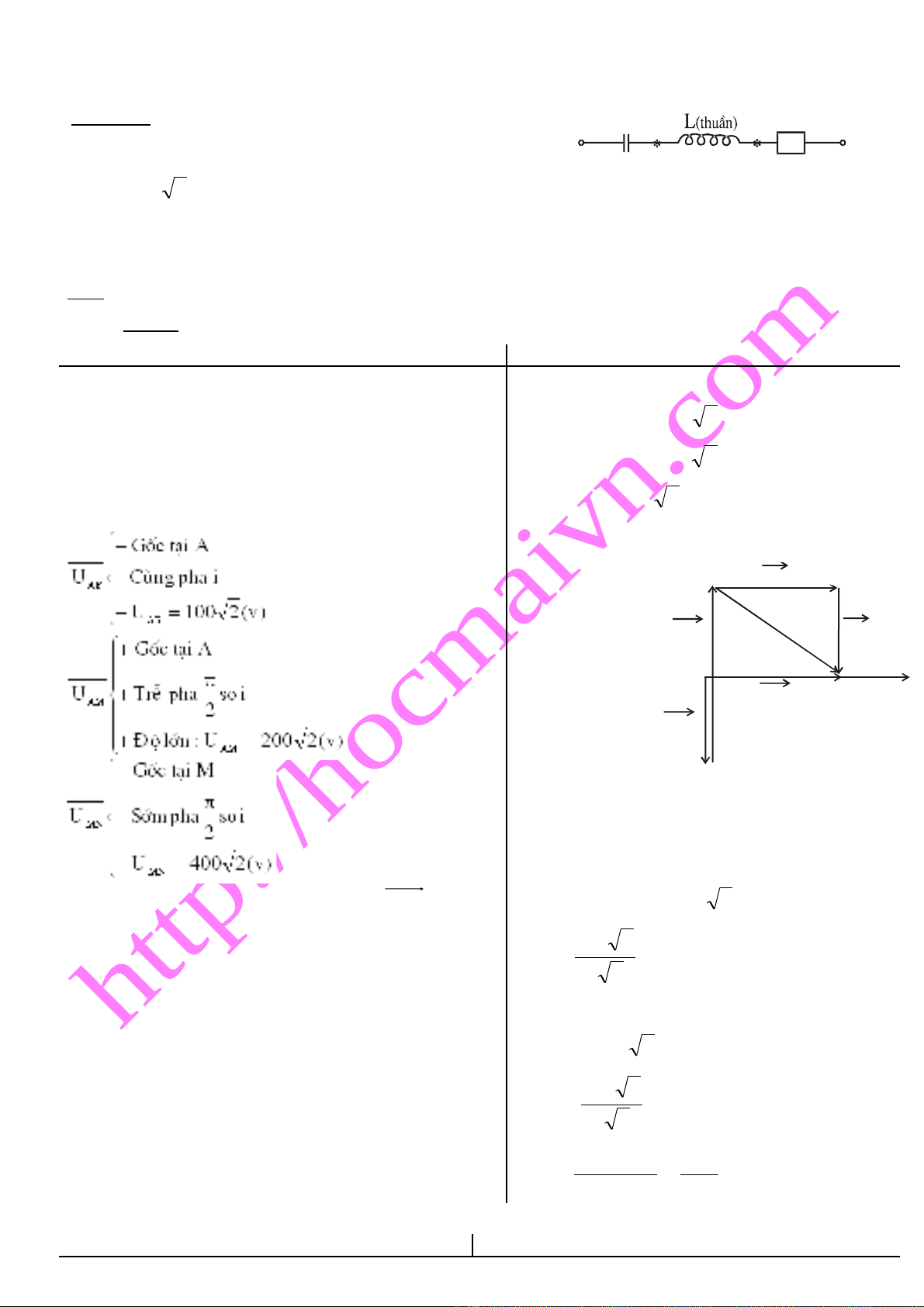
Bài t p 1ậ : Cho m ch đi n nh hình vạ ệ ư ẽ:
UAB = 200cos100πt(V) ZC = 100Ω ; ZL = 200Ω
I = 2
)A(2
; cosϕ = 1; X là đo n m ch g m hai trong ba ph n t (Rạ ạ ồ ầ ử 0, L0 (thu n), Cầ0) m c n iắ ố
ti p.ế
H i X ch a nh ng linh ki n gì ? Xác đ nh giá tr c a các linh ki n đó.ỏ ứ ữ ệ ị ị ủ ệ
Gi iả
Cách 1: Dùng ph ng pháp gi n đ véc t tr t.ươ ả ồ ơ ượ
H ng d nướ ẫ L i gi iờ ả
B1: V gi n đ véc t cho đo n m ch đã bi tẽ ả ồ ơ ạ ạ ế
+ Ch n tr c c ng đ dòng đi n làm tr c g c, A làọ ụ ườ ộ ệ ụ ố
đi m g c.ể ố
+ Bi u di n các hi u đi n th uể ễ ệ ệ ế AB; uAM; uMN b ng cácằ
véc t t ng ng.ơ ươ ứ
* Theo bài ra cosϕ = 1 ⇒ uAB và i cùng pha.
UAM = UC = 200
2
(V)
UMN = UL = 400
2
(V)
UAB = 100
2
(V)
Gi n đ véc t tr tả ồ ơ ượ
Vì UAB cùng pha so v i i nên trên NB (h p X)ớ ộ
ph i ch a đi n tr Rả ứ ệ ở o và t đi n Cụ ệ o.
B2: Căn c vào d ki n c a bài toán ứ ữ ệ ủ ⇒
N B
U
xiên góc
và tr pha so v i i nên X ph i ch a Rễ ớ ả ứ o và Co
B3: D a vào gi n đ ự ả ồ ⇒ URo và UCo t đó tính Rừo; Co
+ URo = UAB ↔ IRo = 100
2
→ Ro =
)(50
22
2100 Ω=
+ UCo = UL - UC
→ I . ZCo = 200
2
→ ZCo =
)(100
22
2200 Ω=
⇒ Co =
)F(
10
100.100
14
π
=
π
−
Cách 2: Dùng ph ng pháp đ i sươ ạ ố
H ng d nướ ẫ L i gi iờ ả
Biên so n và gi ng d y: Lê Tr ng Duy - http://hocmaivn.comạ ả ạ ọ
B1: Căn c ứ“Đ u vào”ầ c a bài toán đ đ t các giủ ể ặ ả
thi t có th x y ra.ế ể ả
→ Trong X có ch a Rứo&Lo ho c Rặo và Co
B2: Căn c ứ“Đ u ra”ầ đ lo i b các gi thi tể ạ ỏ ả ế
không phù h p vì ZợL > ZC nên X ph i ch a Cả ứ o.
B3: Ta th y X ch a Rấ ứ o và Co phù h p v i gi thi tợ ớ ả ế
đ t ra.ặ
* Theo bài ZAB =
)(50
22
2100 Ω=
1
Z
R
cos ==ϕ
Vì trên AN ch có C và L nên NB (trong X) ph i ch aỉ ả ứ
Ro, m t khác: Rặo=Z → ZL(t ng) = ZổC(t ng) nên ZổL =
ZC+ZCo
V y X có ch a Rậ ứ o và Co
Ω=−=−=
Ω==
)(100100200ZZZ
)(50ZR
CLC
AB0
o
⇒ Co =
)F(
10 4
π
−
Nh n xét:ậ Trên đây là m t bài t p còn khá đ n gi n v h p kín, trong bài này đã cho bi t ộ ậ ơ ả ề ộ ế ϕ và
I, chính vì v y mà gi i theo ph ng pháp đ i s có ph n d dàng. Đ i v i nh ng bài toán v h p kínậ ả ươ ạ ố ầ ễ ố ớ ữ ề ộ
ch a bi t ư ế ϕ và I thì gi i theo ph ng pháp đ i s s g p khó khăn, n u gi i theo ph ng pháp gi nả ươ ạ ố ẽ ặ ế ả ươ ả
đ véc t tr t s thu n l i h n r t nhi u. Ví d 2 sau đây là m t bài toán đi n hình.ồ ơ ượ ẽ ậ ợ ơ ấ ề ụ ộ ể
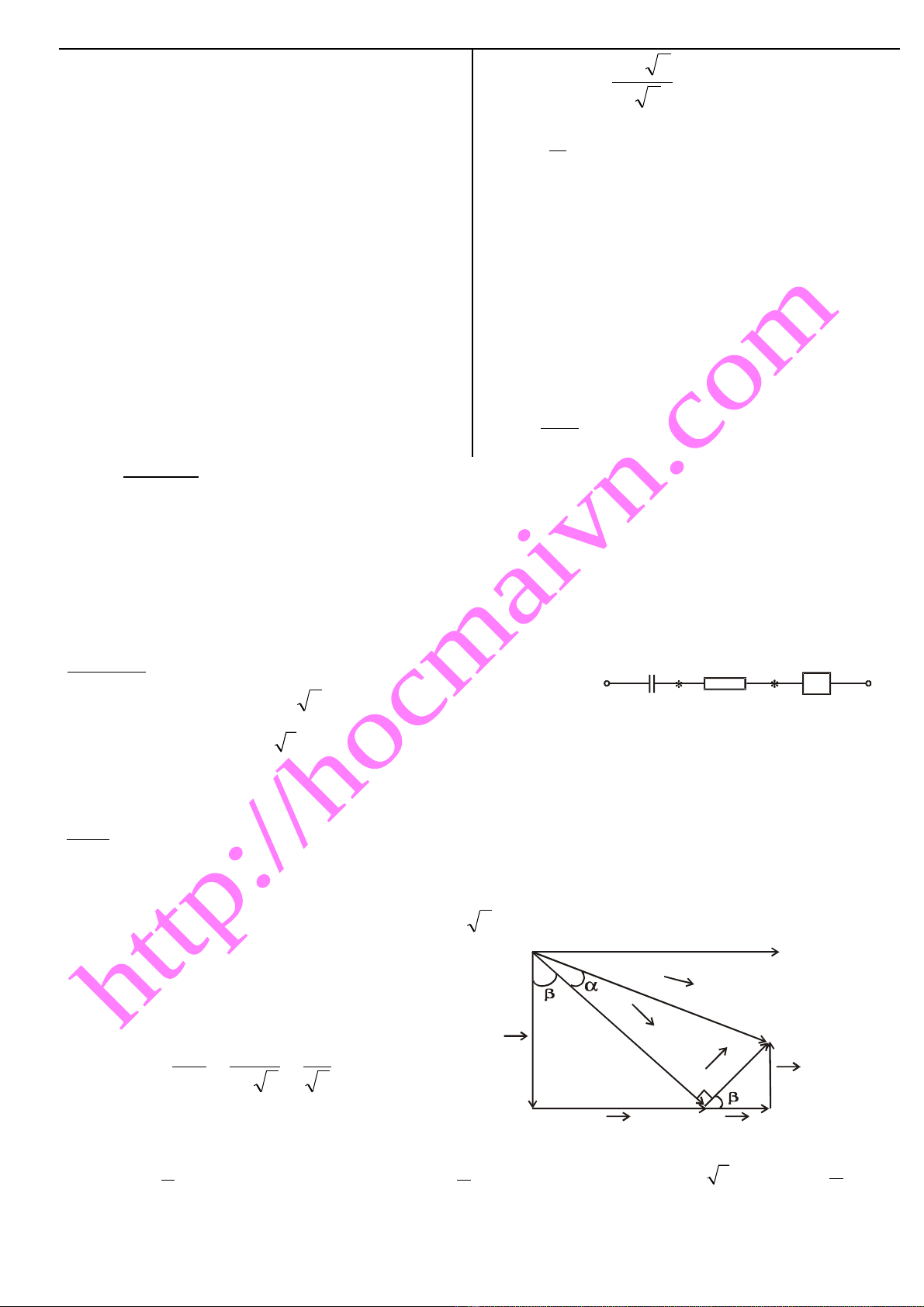
Bài t p 2:ậ Cho m ch đi n nh hình vạ ệ ư ẽ
UAB = 120(V); ZC =
)(310 Ω
R = 10(Ω); uAN = 60
6 cos100 ( )t v
π
UAB = 60(v)
a. Vi t bi u th c uế ể ứ AB(t)
b. Xác đ nh X. Bi t X là đo n m ch g m hai trong ba ph n t (Rị ế ạ ạ ồ ầ ử o, Lo (thu n), Cầo) m c n i ti pắ ố ế
Gi iả :
a. V gi n đ véc t cho đo n m ch đã bi t Aẽ ả ồ ơ ạ ạ ế
Ph n còn l i ch a bi t h p kín ch a gì vì v y ta gi s nó là m t véc t b t kỳ ti n theo chi uầ ạ ư ế ộ ứ ậ ả ử ộ ơ ấ ế ề
dòng đi n sao cho: NB = 60V, AB = 120V, AN = 60ệ
V3
+ Xét tham giác ANB, ta nh n th yậ ấ
AB2 = AN2 + NB2, v y đó là tam giác vuông t iậ ạ
N
tgα =
3
1
360
60
AN
NB ==
⇒
6
π
=α
⇒ UAB s m pha so v i Uớ ớ AN 1 góc
6
π
→ Bi u th c uể ứ AB(t): uAB= 120
2 cos 100 6
t
π
π
+
(V)
Biên so n và gi ng d y: Lê Tr ng Duy - http://hocmaivn.comạ ả ạ ọ
A
C
B
N
M
X
R
U
AB
U
C
U
R
A
MN
B
i
U
AN
U
NB
U
R
0
U
l
0
D
A
C
B
N
M
X
R
b. Xác đ nh Xị
T gi n đ ta nh n th y ừ ả ồ ậ ấ
NB
chéo lên mà trong X ch ch a 2 trong 3 ỉ ứ ph n t nên X ph i ch aầ ử ả ứ
Ro và Lo. Do đó ta v thêm đ c ẽ ượ
00 LR UvµU
nh hình v .ư ẽ
+ Xét tam giác vuông AMN:
6
3
1
Z
R
U
U
tg
CC
Rπ
=β⇒===β
+ Xét tam giác vuông NDB
)V(30
2
1
.60sinUU
)V(330
2
3
.60cosUU
N BL
N BR
O
O
==β=
==β=
M t khác: UặR = UANsinβ = 60
)v(330
2
1
.3 =
π
=
π
=⇒Ω===
Ω===
⇒
==⇒
)H(
3
1,0
3100
10
L)(
3
10
33
30
I
U
Z
)(10
33
330
I
U
R
)A(33
10
330
I
O
L
L
R
O
O
O
O
* Nh n xét:ậ Đây là bài toán ch a bi t tr c pha và c ng đ dòng đi n nên gi i theo ph ngư ế ướ ườ ộ ệ ả ươ
pháp đ i s s g p r t nhi u khó khăn (ph i xét nhi u tr ng h p, s l ng ph ng trình l n ạ ố ẽ ặ ấ ề ả ề ườ ợ ố ượ ươ ớ → gi iả
r t ph c t p). Nh ng khi s d ng gi n đ véc t tr t s cho k t qu nhanh chóng, ng n g n, ... Tuyấ ứ ạ ư ử ụ ả ồ ơ ượ ẽ ế ả ắ ọ
nhiên cái khó c a h c sinh là ch r t khó nh n bi t đ c tính ch t ủ ọ ở ỗ ấ ậ ế ượ ấ
2
N B
2
AN
2
AB UUU +=
. Đ có sể ự
nh n bi t t t, h c sinh ph i rèn luy n nhi u bài t p đ có kĩ năng gi i.ậ ế ố ọ ả ệ ề ậ ể ả
Bài t p ậ 3 Cho m ch đi n nh hình vạ ệ ư ẽ:
UAB = cost; uAN = 180
2 cos 100 ( )
2
t V
π
π
−
ZC =
90(Ω); R = 90(Ω); uAB =
60 2 cos100 ( )t V
π
a. Vi t bi u th c uế ể ứ AB(t)
b. Xác đ nh X. Bi t X là đo n m ch g m hai trong ba ph n t (Rị ế ạ ạ ồ ầ ử O, Lo (thu n), CầO) m c n iắ ố
ti p.ế
Phân tích bài toán: Trong ví d 3 này ta ch a bi t c ng đ dòng đi n cũng nh đ l ch phaụ ư ế ườ ộ ệ ư ộ ệ
c a các hi u đi n th so v i c ng đ dòng đi n nên gi i theo ph ng pháp đ i s s g p nhi u khóủ ệ ệ ế ớ ườ ộ ệ ả ươ ạ ố ẽ ặ ề
khăn. Ví d 3 này cũng khác ví d 2 ch ch a bi t tr c Uụ ụ ở ỗ ư ế ướ AB có nghĩa là tính ch t đ c bi t trong víấ ặ ệ
Biên so n và gi ng d y: Lê Tr ng Duy - http://hocmaivn.comạ ả ạ ọ
d 2 không s d ng đ c. Tuy nhiên ta l i bi t đ l ch pha gi a uụ ử ụ ượ ạ ế ộ ệ ữ AN và uNB, có th nói đây là m u ch tể ấ ố
đ gi i toán.ể ả
Gi iả
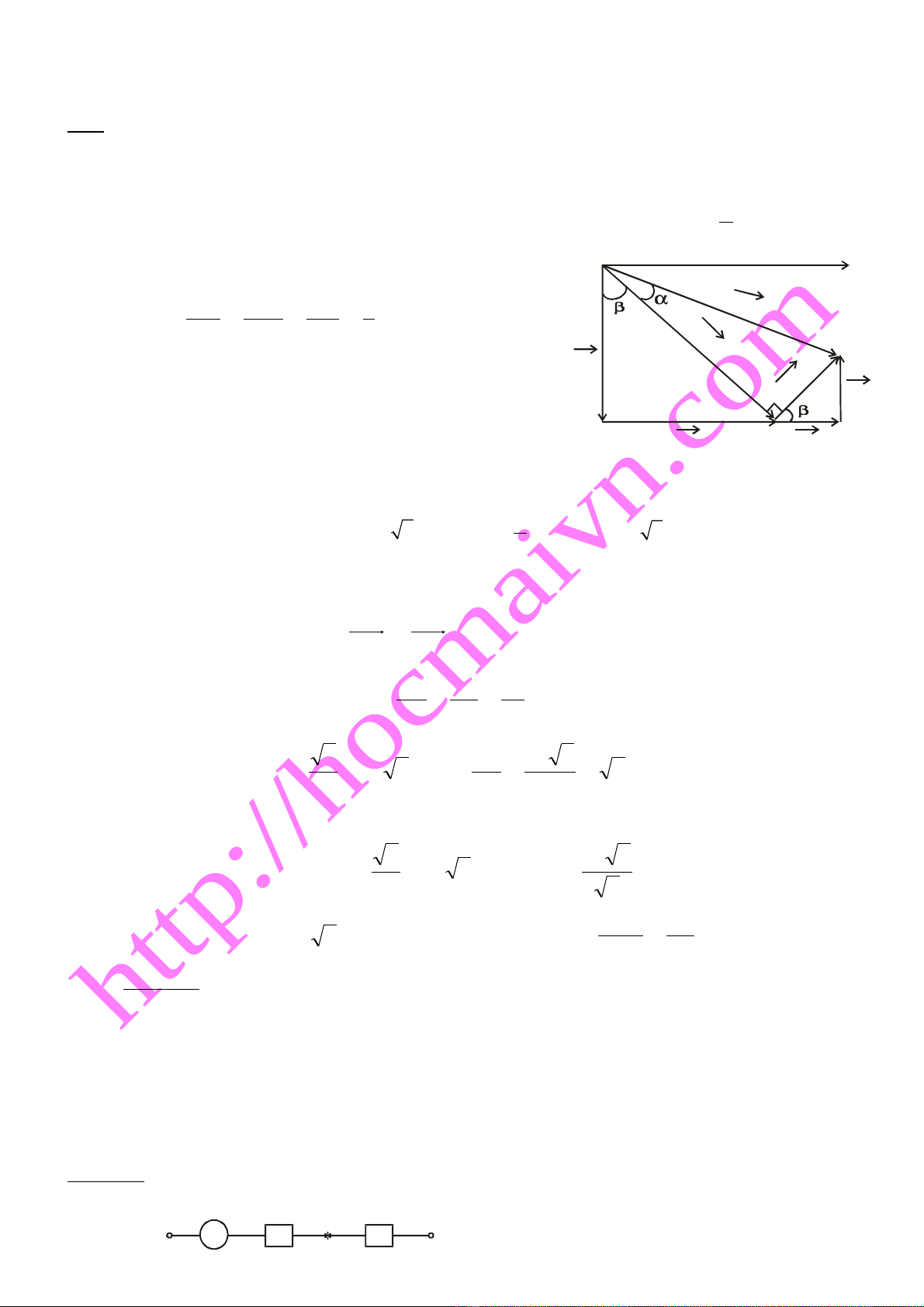
a. V gi n đ véc t cho đo n m ch đã bi t AN. Ph n còn l i ch a bi t h p kín ch a gì, vìẽ ả ồ ơ ạ ạ ế ầ ạ ư ế ộ ứ
v y ta gi s nó là m t véc t b t kỳ ti n theo chi u dòng đi n sao cho uậ ả ử ộ ơ ấ ế ề ệ NB s m pha ớ
2
π
so v i uớAN
+ Xét tam giác vuông ANB
* tgα =
3
1
180
60
U
U
AN
NB
AN
N B ===
⇒ α ≈ 800 = 0,1π(rad)
⇒ uAB s m pha so v i uớ ớ AN m t góc 0,1ộπ
*
2
N B
2
AN
2
AB UUU +=
= 1802 + 602 ≈ 1900 ⇒ UAb = 190(V)
→ bi u th c uể ứ AB(t): uAB =
190 2 cos 100 0,1
2
t
π
π π
− +
=
( )
190 2 cos 100 0,4 ( )t V
π π
−
b. T gi n đ ta nh n th y NB chéo lên mà trong X ch ch a hai trong 3 ph n t trên X ph iừ ả ồ ậ ấ ỉ ứ ầ ử ả
ch a RứO
và LO. Do đó ta v thêm đ c ẽ ượ
OO LR UvµU
nh hình v .ư ẽ
+ Xét tam giác vuông AMN:
1
90
90
Z
R
U
U
tg
CC
R====β
⇒ β = 450
⇒ UC = UAN.cosβ = 180.
)A(2
90
290
Z
U
I290
2
2
C
C===⇒=
+ Xét tam giác vuông NDB
)(30
2
230
R)V(230
2
2
.60cosUU 0N BR OΩ==⇒==β=
β = 450 ⇒ ULo = URo= 30
2
(V) → ZLo = 30(Ω)
)H(
3,0
100
30
LOπ
=
π
=⇒
Nh n xét:ậ Qua ba thí d trên ta đã hi u đ c ph n nào v ph ng pháp gi i bài toán h p kínụ ể ượ ầ ề ươ ả ộ
b ng gi n đ véc t tr t, cũng nh nh n ra đ c u th c a ph ng pháp này. Các bài t p ti p theoằ ả ồ ơ ượ ư ậ ượ ư ế ủ ươ ậ ế
tôi s đ c p đ n bài toán có ch a 2 ho c 3 h p kín, ta s th y rõ h n n a u th v t tr i c aẽ ề ậ ế ứ ặ ộ ẽ ấ ơ ữ ư ế ượ ộ ủ
ph ng pháp này.ươ
Bài t p 4 ậ M t ộm ch đi n xoay chi u có s đ nh hình vạ ệ ề ơ ồ ư ẽ.
Trong h p X và Y ch có m t linh ki nộ ỉ ộ ệ
ho c đi n tr , ho c cu n c m, ho c là t đi n.ặ ệ ở ặ ộ ả ặ ụ ệ
Biên so n và gi ng d y: Lê Tr ng Duy - http://hocmaivn.comạ ả ạ ọ
U
AB
U
C
U
R
A
MN
B
i
U
AN
U
NB
U
R
0
U
c
0
D
Ampe k nhi t (a) ch 1A; Uế ệ ỉ AM = UMB = 10V
UAB = 10
V3
. Công su t tiêu th c a đo n m ch AB là P = 5ấ ụ ủ ạ ạ
6
W. Hãy xác đ nh linh ki nị ệ
trong X và Y và đ l n c a các đ i l ng đ c tr ng cho các linh ki n đó. Cho bi t t n s dòng đi nộ ớ ủ ạ ượ ặ ư ệ ế ầ ố ệ
xoay chi u là f = 50Hz.ề
* Phân tích bài toán: Trong bài toán này ta có th bi t đ c góc l ch ể ế ượ ệ ϕ (Bi t U, I, P ế→ ϕ)
nh ng đo n m ch ch ch a hai h p kín. Do đó n u ta gi i theo ph ng pháp đ i s thì ph i xét r tư ạ ạ ỉ ứ ộ ế ả ươ ạ ố ả ấ
nhi u tr ng h p, m t tr ng h p ph i gi i v i s l ng r t nhi u các ph ng trình, nói chung làề ườ ợ ộ ườ ợ ả ả ớ ố ượ ấ ề ươ
vi c gi i g p khó khăn. Nh ng n u gi i theo ph ng pháp gi n đ véc t tr t s tránh đ c nh ngệ ả ặ ư ế ả ươ ả ồ ơ ượ ẽ ượ ữ
khó khăn đó. Bài toán này m t l n n a l i s d ng tính ch t đ c bi t c a tam giác đó là: U = Uộ ầ ữ ạ ử ụ ấ ặ ệ ủ MB;
UAB = 10
AM
U3V3 =
→ tam giác AMB là ∆ cân có 1 góc b ng 30ằ0.
Gi iả :
H s công su t: ệ ố ấ
UI
P
cos =ϕ
42
2
310.1
65
cos π
±=ϕ⇒==ϕ⇒
* Tr ng h p 1: uườ ợ AB s m pha ớ
4
π
so v i i ớ⇒ gi n đ véc tả ồ ơ Vì:
=
=
AMAB
M BAM
U3U
UU
⇒ ∆AMB là ∆ cân và UAB = 2UAMcosα ⇒ cosα =
10.2
310
U2
U
AM
AB =
⇒ cosα =
0
30
2
3=α⇒
a. uAB s m pha h n uớ ơ AM m t góc 30ộ0
⇒ UAM s m pha h n so v i i 1 góc ớ ơ ớ ϕX = 450 - 300 = 150
⇒ X ph i là 1 cu n c m có t ng tr Zả ộ ả ổ ở X g m đi n tr thu n Rồ ệ ở ậ X và đ t c m Lộ ự ả X
Ta có:
)(10
1
10
I
U
ZAM
XΩ===
Xét tam giác AHM:
+
0
XX
0
XR 15cosZR15cosUU X=⇒=
⇒ RX = 10.cos150 = 9,66(Ω)
+
)(59,215sin1015sinZZ15sinUU 00
XL
0
XL XX Ω===⇒=
)m H(24,8
100
59,2
LX=
π
=⇒
Xét tam giác vuông MKB: MBK = 150 (vì đ i x ng)ố ứ
⇒ UMB s m pha so v i i m t góc ớ ớ ộ ϕY = 900 - 150 = 750
⇒ Y là m t cu n c m có đi n tr Rộ ộ ả ệ ở Y và đ t c m Lộ ự ả Y
Biên so n và gi ng d y: Lê Tr ng Duy - http://hocmaivn.comạ ả ạ ọ
i
M
U
R
X
U
L
X
K
U
AB
U
Y
U
R
Y
U
L
Y
AH
B
45
0
30
0
15
0
U
i
B
K
M
H
A
U
AB
U
R
Y
U
X
U
L
Y
U
R
X
U
L
X
30
0
45
0
U
Y