12/25/2008
1
Nguyn Quang Minh
0
....
..
........
...
..
0
....
...
............
...
...
/1000
0..00
00/10
000/1
...
............
...
...
222
111
2
1
321
21
21
=
+
=
+
=+
=
+
−
r
b
a
r
b
a
r
b
a
r
b
a
nnnn
n
n
K
K
K
p
rr
p
br
p
ar
p
br
p
bb
p
ab
p
ar
p
ab
p
aa
K
K
K
rba
rba
rba
p
p
p
rrr
bbb
aaa
ω
ω
ω
ω
ω
ω


12/25/2008
2
=+
++
+
=+
++
+
=+
++
+
=+
=
+
−
0...
....
0...
0...
rrba
brba
arba
K
p
rr
K
p
br
K
p
ar
K
p
br
K
p
bb
K
p
ab
K
p
ar
K
p
ab
K
p
aa
ω
ω
ω


[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
( )
acba
ccba
bcba
acba
rrba
brba
arba
KtacKtab
taa
K
KtccKtbcKtaa
KtbcKtbbKtaa
KtacKtabKtaa
KtrrKtbrKtaa
KtbrKtbbKtaa
KtarKtabKtaa
ω
ω
ω
ω
ω
ω
ω
++−=
=+++
=+++
=+++
=++++
=++++
=++++
=+
=
+
−
1
0
0
0
0...
....
0...
0...


12/25/2008
3
[
]
[
]
[
]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
( )
[ ] [ ]
[ ][ ] [ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
[ ][ ] [ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
[ ] [ ]
[ ] [ ]
( )
[ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
2.
02.
01.
1.
1.
1.
1.
1.
1.
1.
1
01.1.
01.1.
0
0
1
0
0
0
2.
2.
1.
1.
1.
1.
1.
tcc
KKtcc
tbc
tbb
Ktbc
tbb
tbc
tcc
Ktbc
tbb
K
KtccKtbc
KtbcKtbb
tac
taa
Ktac
taa
tab
tccKtac
taa
tab
tbc
tab
taa
Ktab
taa
tac
tbcKtab
taa
tab
tbb
KtacKtab
taa
K
KtccKtbcKtac
KtbcKtbbKtab
KtacKtabKtaa
c
ccc
b
cc
bcb
ccb
bcb
a
ccb
a
bcb
acba
ccba
bcba
acba
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=⇒=+
=
−+
−
+−=
=++
=++
=
−+
−+
−
=
−+
−+
−
++−=
=+++
=+++
=
+
+
+
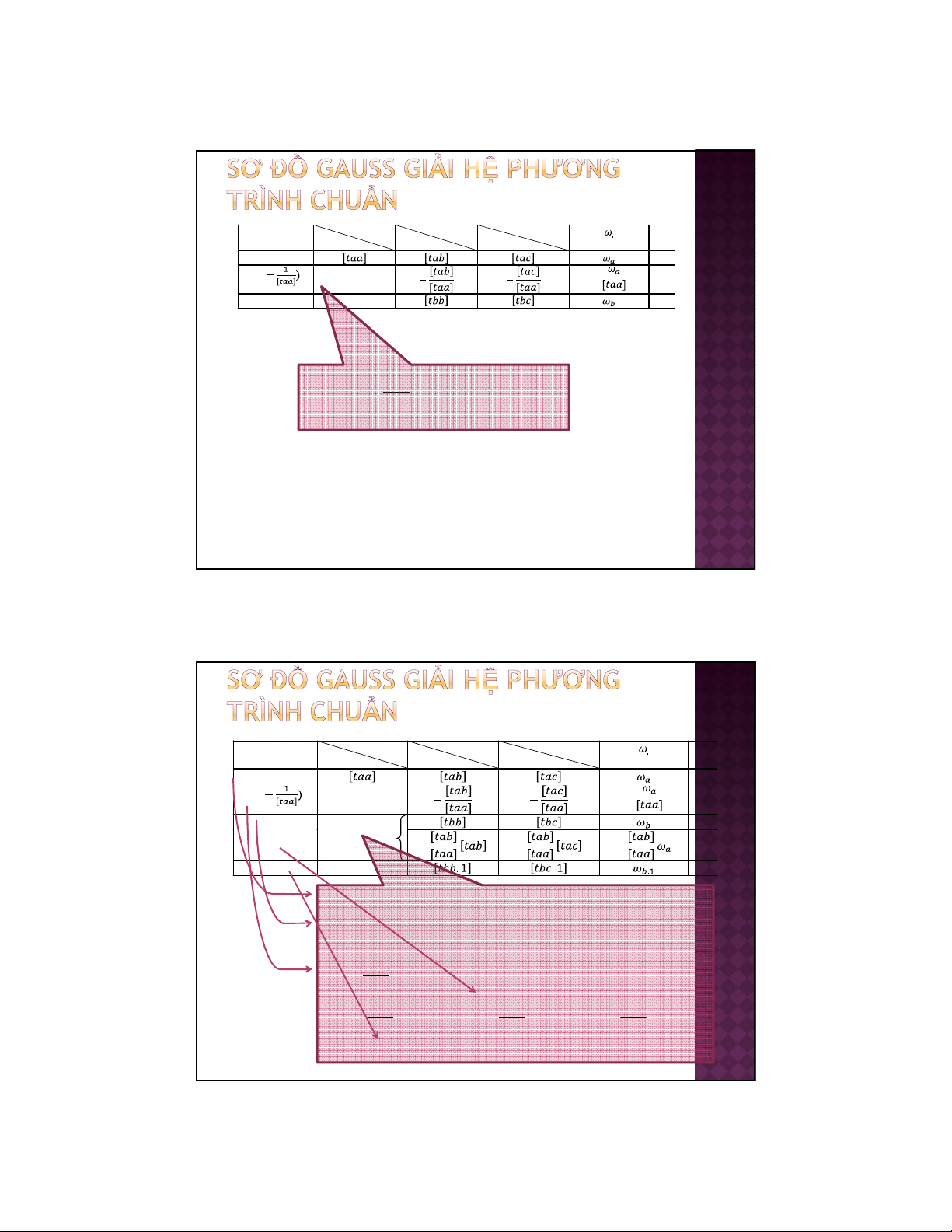
Ký hiu dòng a K
a
b K
a
c K
c
a
E
1
(
-
1
K
a
b
E
1b
×a
b.1
E
2
(
-
1
K
b
c
E
1c
×a
E
2c
×b.1
c.2
E
3
-
1
K
c
K
a
K
b
K
c
12/25/2008
4
Ký hi
u
dòng
a
K
a
b K
a
c K
c
a
E
1
(
-
1
K
a
b
[ ] [ ] [ ]
( )
acba
KtacKtab
taa
K
ω
++−=
1
Ký hi
u
dòng
a
K
a
b K
a
c K
c
a
E
1
(
-
1
K
a
b
E
1b
×a
b.1
[
]
[
]
[
]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
( )
[ ] [ ]
[ ][ ] [ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
01.1.
0
1
0
0
0
1.
=++
=
−+
−+
−
++−=
=+++
=+++
=
+
+
+
bcb
a
bcb
acba
ccba
bcba
acba
KtbcKtbb
tab
taa
Ktab
taa
tac
tbcKtab
taa
tab
tbb
KtacKtab
taa
K
KtccKtbcKtac
KtbcKtbbKtab
K
tac
K
tab
K
taa
ω
ω
ω
ω
ω
ω
ω
12/25/2008
5
Ký hiu dòng a
K
a
b K
a
c K
c
a
E
1
(
-
1
K
a
b
E
1b
×a
b.1
E
2
(
-
1
K
b
c
E
1c
×a
E
2c
×b.1
c.2
E
3
-
1
K
c
K
a
K
b
K
c
[
]
[
]
[
]
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ] [ ] [ ]
( )
[ ] [ ]
[ ][ ] [ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
[ ][ ] [ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
[ ] [ ]
[ ] [ ]
( )
[ ] [ ]
[ ][ ] [ ][ ]
[ ] [ ]
2.
02.
01.
1.
1.
1.
1.
1.
1.
1.
1
01.1.
01.1.
0
0
1
0
0
0
2.
2.
1.
1.
1.
1.
1.
tcc
KKtcc
tbc
tbb
Ktbc
tbb
tbc
tcc
Ktbc
tbb
K
KtccKtbc
KtbcKtbb
tac
taa
Ktac
taa
tab
tccKtac
taa
tab
tbc
tab
taa
Ktab
taa
tac
tbcKtab
taa
tab
tbb
KtacKtab
taa
K
KtccKtbcKtac
KtbcKtbbKtab
KtacKtabKtaa
c
ccc
b
cc
bcb
ccb
bcb
a
ccb
a
bcb
acba
ccba
bcba
acba
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=⇒=+
=
−+
−
+−=
=++
=++
=
−+
−+
−
=
−+
−+
−
++−=
=+++
=+++
=
+
+
+