
Chöông 2
HE
HEÄÄTO
TOÏÏA
A Ñ
ÑO
OÄÄ
THAM CHIE
THAM CHIEÁÁU D
U DÖ
ÖÕ LIE
Õ LIEÄÄU
U
KHOÂNG GIAN
KHOÂNG GIAN
Bieân soaïn: GV. Phaïm Theá Huøng
2.1. GIÔ
2.1. GIÔÙÙI THIE
I THIEÄÄU
U
Thoâng tin ñòa lyù laø thoâng tin veà thuoäc tính vaø vò trí
cuûa caùc ñoái töôïng treân beà maët traùi ñaát.
Ñeå coù thoâng tin veà vò trí cuûa caùc ñoái töôïng treân
beà maët traùi ñaát ngöôøi ta tieán haønh laäp moâ hình bieåu
dieãn traùi daát vaø xaùc laäp moät heä toïa ñoä treân ñoù.
Vò trí cuûa ñoái töôïng treán traùi ñaát hoaøn toaøn ñöôïc
xaùc ñònh thoâng qua caùc giaù trò toïa ñoä trong heä toïa
ñoä xaùc laäp treân ñoù.

Bieân soaïn: GV. Phaïm Theá Huøng
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
Traùi ñaát coù hình daïng nhö theá naøo?
Bieân soaïn: GV. Phaïm Theá Huøng
Ñònh nghóa: Geoid laø maët nöôùc bieån trung
bình yeân tónh, keùo daøi xuyeân qua caùc luïc
ñòa vaø haûi ñaûo taïo thaønh moät beà maët cong
kheùp kín.
Tính chaát: Taïi baát kyø moät ñieåm naøo treân maët
Geoid, phaùp tuyeán cuõng luoân luoân truøng vôùi
phöông cuûa daây doïi qua ñieåm ñoù.
ÖÙng duïng: Duøng ñeå ño cheânh cao
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
2.2.1. Moâ hình Geoid

Bieân soaïn: GV. Phaïm Theá Huøng
Geoid laø beà maët ñaëc
tröng cho hình daïng cuûa
Traùi ñaát vaø khoù coù theå bieåu
dieãn bôûi moät hình daïng
toaùn hoïc naøo
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
2.2.1. Moâ hình Geoid
Bieân soaïn: GV. Phaïm Theá Huøng
Phöông phaùp thaønh laäp: xoay moät hình
ellipse quanh baùn truïc nhoû cuûa noù vôùi kích
thöôùc xaáp xæ Geoid.
Caùc thoâng soá cô baûn: baùn truïc lôùn (a), baùn
truïc nhoû (b), ñoä deït (f hoaëc )
f = (a – b)/a
Coù hai loaïi ellipsoid: ellipsoid Traùi ñaát (toaøn
caàu) vaø ellipsoid tham chieáu (ñòa phöông).
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
2.2.2. Moâ hình Ellipsoid
Bieân soaïn: GV. Phaïm Theá Huøng
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
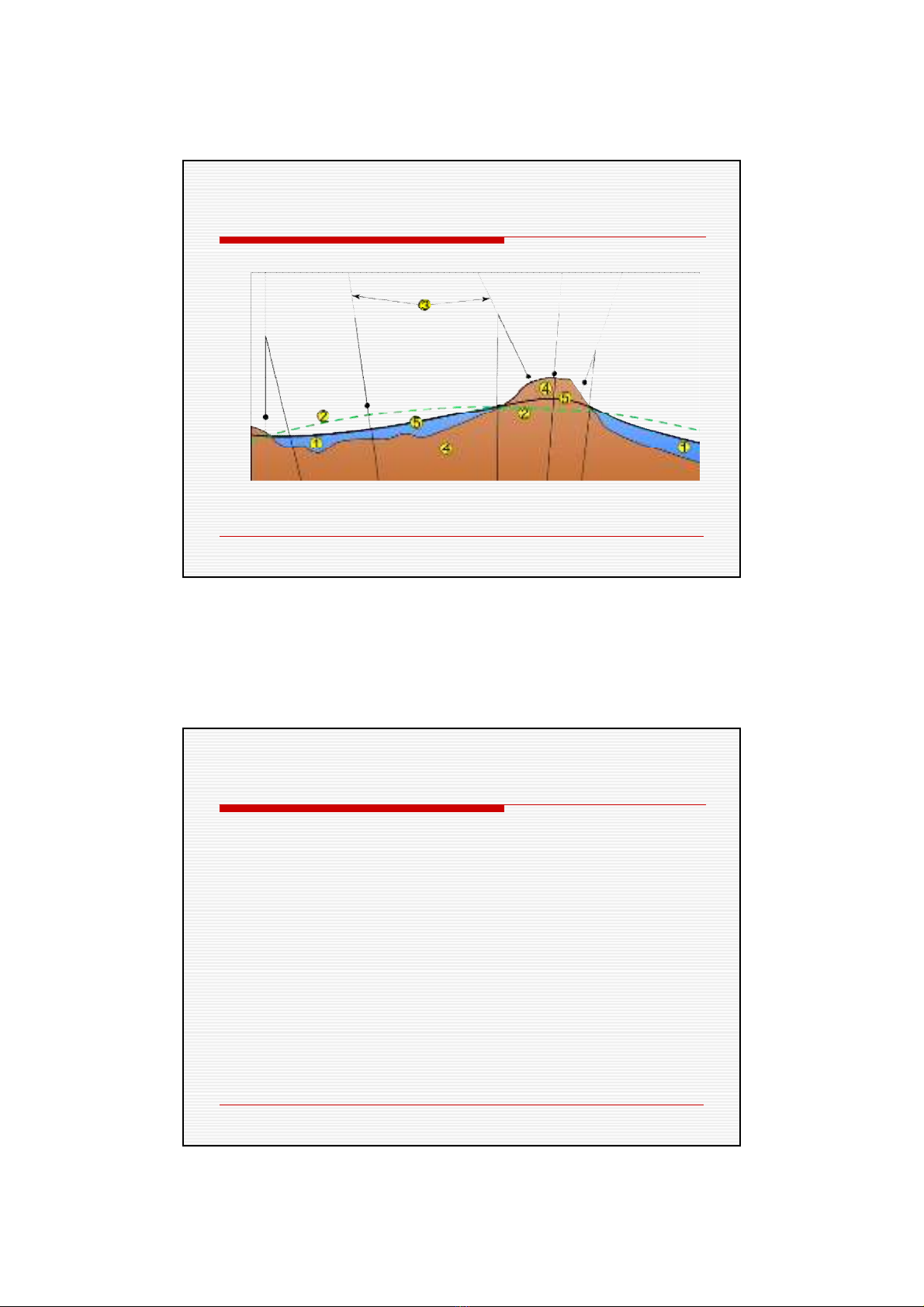
2.2.2. Moâ hình Ellipsoid
Stt Ellipsoid Baùn truïc lôùn
a (m) Nghòch ñaûo ñoä deït
(1/f)
1 Clarke 1880 6.378.249,145 293,465
2 Everest 1830 6.377.276,345 300,8017
3 Krasovsky 1940 6.378.245 298,3
5 Helmert 1906 6.378.270 297
6 WGS-84 6.378.137 298,257223563
Bieân soaïn: GV. Phaïm Theá Huøng
Moái quan heä giöõa Traùi ñaát vaø moâ hình bieåu dieãn
Heä toïa ñoä quoác teá
Heä toïa ñoä ñòa phöông
ùBeà maët Traùi ñaát
Beà maët ellipsoid ñòa phöông
Beà maët ellipsoid quoác teá
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
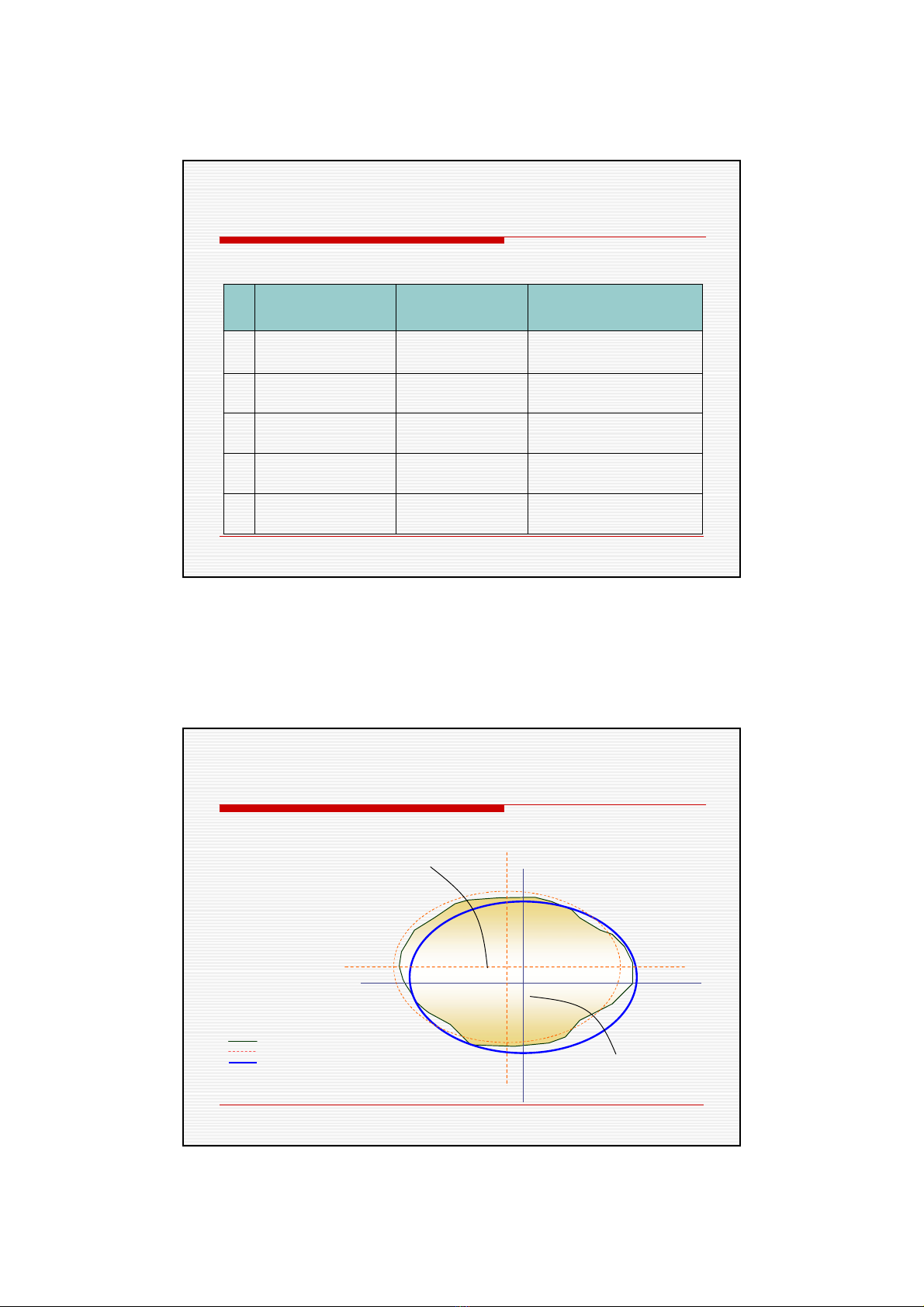
Bieân soaïn: GV. Phaïm Theá Huøng
1. Möïc nöôùc bieån 2. Ellipsoid 3. Phöông daây doïi
4. Luïc ñòa 5. Geoid
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
Moái quan heä giöõa Traùi ñaát vaø moâ hình bieåu dieãn
Bieân soaïn: GV. Phaïm Theá Huøng
Trong traéc ñòa – baûn ñoà: beà maët Traùi ñaát
geoid.
Trong thöïc tieãn: thay baèng ellipsoid.
Ñieàu kieän:
Taâm ellipsoid truøng vôùi troïng taâm Traùi ñaát, maët
phaúng xích ñaïo ellipsoid truøng vôùi maët phaúng
xích ñaïo Traùi ñaát.
Khoái löôïng ellipsoid baèng khoái löôïng Traùi ñaát.
Toång bình phöông caùc cheânh cao giöõa geoid
vaø ellipsoid laø nhoû nhaát.
2.2. MOÂ HÌNH TOA
2.2. MOÂ HÌNH TOAÙÙN HO
N HOÏÏC
C
BIE
BIEÅÅU DIEÃN TRA
U DIEÃN TRAÙÙI
I Ñ
ÑA
AÁÁT
T
Xaây döïng moâ hình toaùn hoïc bieåu dieãn Traùi ñaát


























