CHƯƠNG 2
MÔ HÌNH HI QUI HAI BIN
1
MÔ HÌNH HI QUI HAI BIN
Hi qui ñơn Nguyn Th Minh Hiu
MÔ HÌNH
• E(Y/Xi=0)
⇒
β
1
cho bit giá tr trung bình ca bin ph thuc
iii uXY
+
+
=
21
β
=
=
−
=
)0/(
1iii XuY
β
2
⇒
β
1
cho bit giá tr trung bình ca bin ph thuc
khi giá tr ca bin ñc lp bng 0.
•⇒β2
cho bit khi X tăng lên
1 ñơn v thì giá tr trung
bình ca bin ph thuc
thay ñi (tăng, gim) β2ñơn v.
(
)
dX
X/YdE
2
=β
Hi qui ñơn Nguyn Th Minh Hiu
I. PHƯƠNG PHÁP BÌNH
PHƯƠNG NH NHT
(OLS: ordinary least squares)
Y
Y
e
ˆ
−
=
iii eXY ++= 21
ˆ
ˆ
ββ
3
⇒min (bình phương nh nht)
⇒min
iii
Y
Y
e
ˆ
−
=
iii
eYY += ˆ
∑
2
i
e
2
1 1
21
2
)
ˆˆ
(
i
n
i
n
iii
XYe
∑ ∑
= =
−−=
ββ
Hi qui ñơn
Nguyn Th Minh Hiu
∑
∑
∑
−
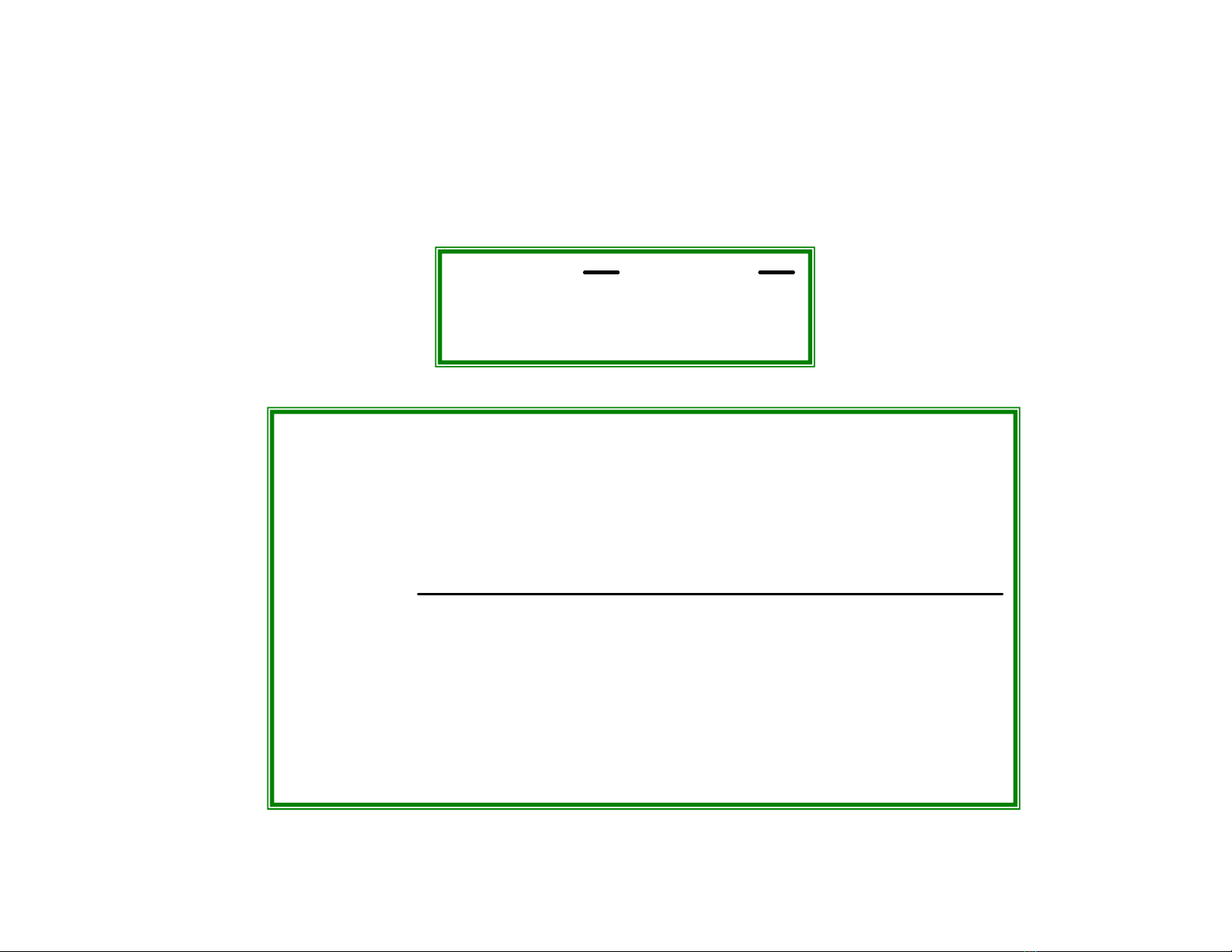
nnn
Y
X
Y
X
n
I.1. Các ưc lưng OLS
1 2
ˆ ˆ
Y X
β β
= −
4
∑ ∑
∑
∑
∑
= =
===
−
−
=
n
i
n
iii
ii
iii
ii
XXn
Y
X
Y
X
n
1
2
1
2
111
2
ˆ
β
Hi qui ñơnNguyn Th Minh Hiu
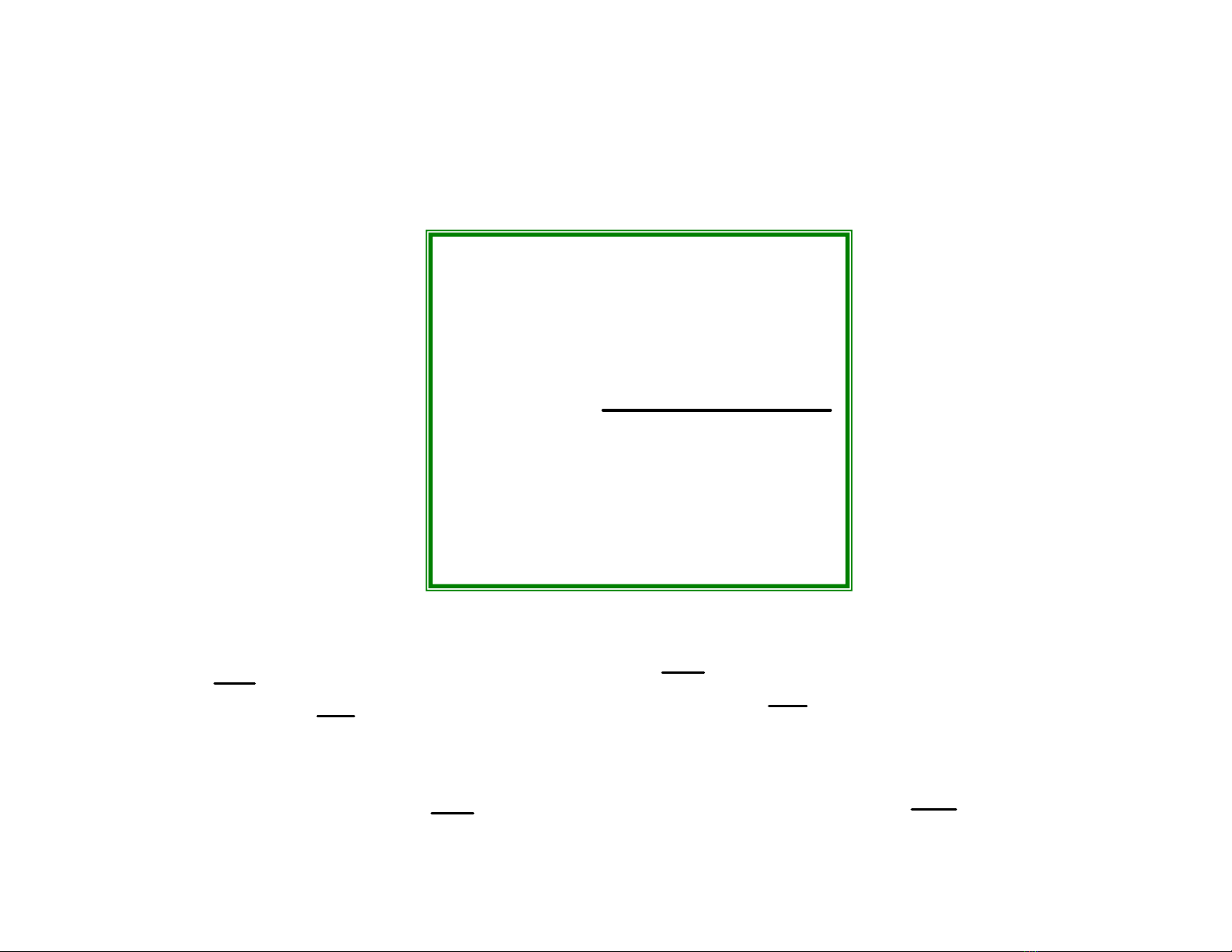
I.1. Các ưc lưng OLS
∑
∑
=
=n
n
iii
x
yx
2
1
2
ˆ
β
Hi qui ñơnNguyn Th Minh Hiu
5
trong ñó:
∑
=ii
x
1
2
∑
=
=
n
1i
i
X
n
1
X
∑
=
=
n
1i
i
Y
n
1
Y
YYy
ii
−= XXx
ii
−=