ĐÁP ÁN Đ THI TUY N SINH Đ I H C 2010Ề Ể Ạ Ọ
MÔN TOÁN – KH I AỐ
I – PH N CHUNG CHO T T C THÍ SINHẦ Ấ Ả
Câu I:
( )
3 2
y x 2x 1 m x m= − + − +
1) B n đ c t gi i.ạ ọ ự ả
2) Ph ng trình hoành đ giao đi m c a đ th hàm s (1) và Oxươ ộ ể ủ ồ ị ố
( )
3 2
x 2x 1 m x m 0− + − + =
( )
( )
2
x 1 x x m 0⇔ − − − =
2
x 1 0 (2)
g(x) x x m 0 (3)
− =
⇔= − − =
G i xọ1 là nghi m pt (2) và xệ2, x3 là nghi m pt (3).ệ
Yê u c u bài toánầ :
( )
2 2 2 2
1 2 3 2 3 2 3
0 1 4m 0
g(1) 0 m 0
x x x 4 1 x x 2x x 0
∆ > + >
≠ ⇔ ≠
+ + < + + − <
1
m1 1
4m 0 m 1
m 0 4 4
m 1 m 0
1 1 2m 4
−
>
− −
< ≠ < <
⇔ ≠ ⇔ ⇔
< ≠
+ + <
Câu II
1)
( )
π
+ + +
=
+
1 sinx cos2x sin x 41cosx
1 tanx 2
. Đi u ki n: ề ệ
≠
≠ −
cosx 0
tanx 1
pt
( ) ( )
+ + +
⇔ =
+
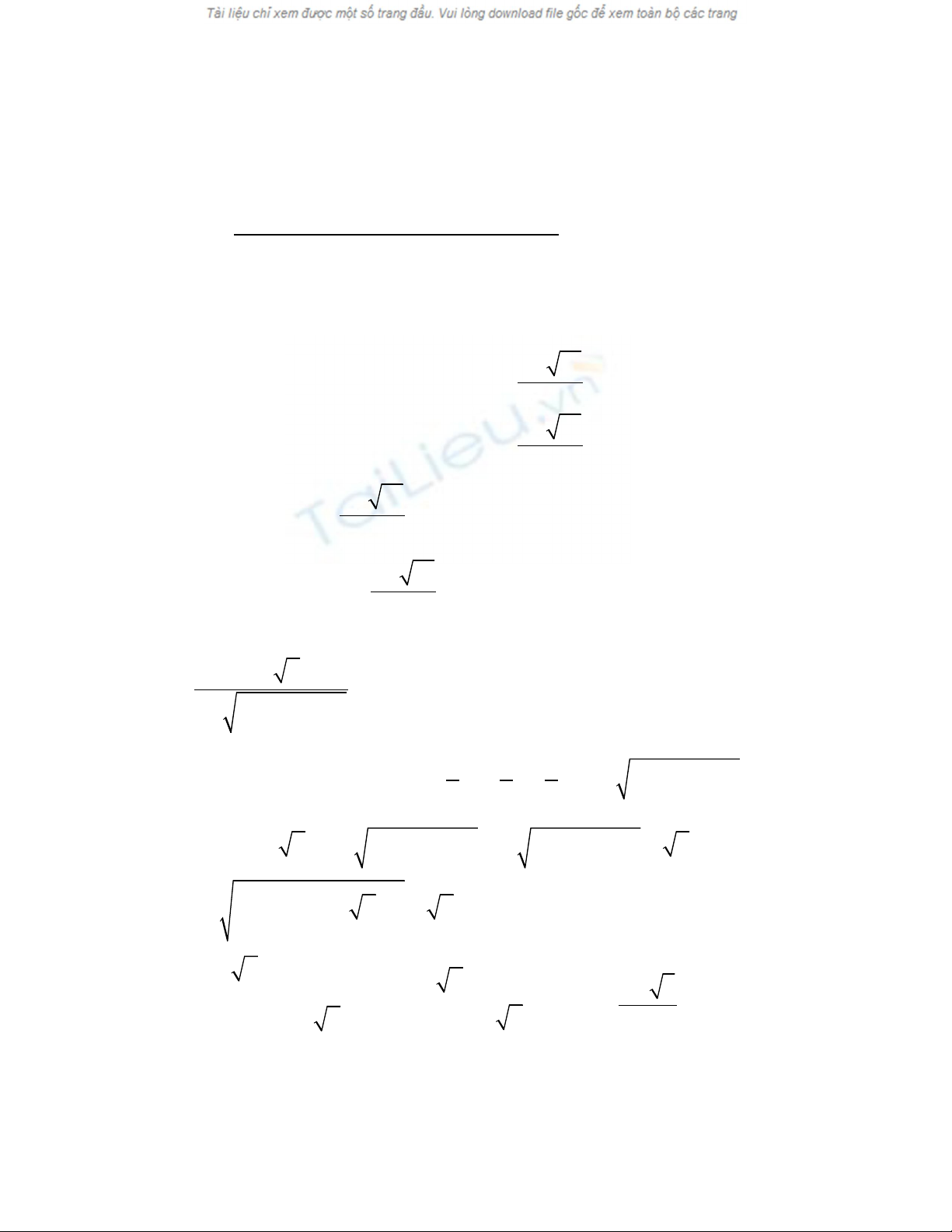
cosx 1 sinx cos2x sinx cosx cosx
cosx sinx
⇔ + + =1 sinx cos2x 0
⇔ + =
2
2cos x sinx 0
( )
⇔ − + =
2
2 1 sin x sinx 0
⇔ − − =
2
2sin x sinx 2 0
+
=
⇒−
=
1 17
sinx >1 (loaïi)
4
1 17
sinx (thoûa ñk)
4
( )
−
= + π
⇒ ∈
−
= π− + π
1 17
x arcsin k2
4k Z
1 17
x arcsin k2
4
.
2)
( )
−≥
− − +
2
x x 1
1 2 x x 1
Ta có:
( ) ( )
− + = − + ≥ ⇒ − − + <
2
2 2
1 3 3
2 x x 1 2 x 1 2 x x 1 0
2 4 2
bpt
( )
⇔ − ≤ − − +
2
x x 1 2 x x 1
( )
( )
⇔ − + ≤ + −
2
2 x x 1 x 1 x
( )
( )
( )
⇔ − + ≤ + −
2
2
2 1 x x x 1 x
( )
( )
( )
+ − ≥
⇔− − ≤
2
x 1 x 0
1 x x 0
+ − ≥
⇔− =
x 1 x 0
1 x x
−
⇒ = 3 5
x2
Câu III
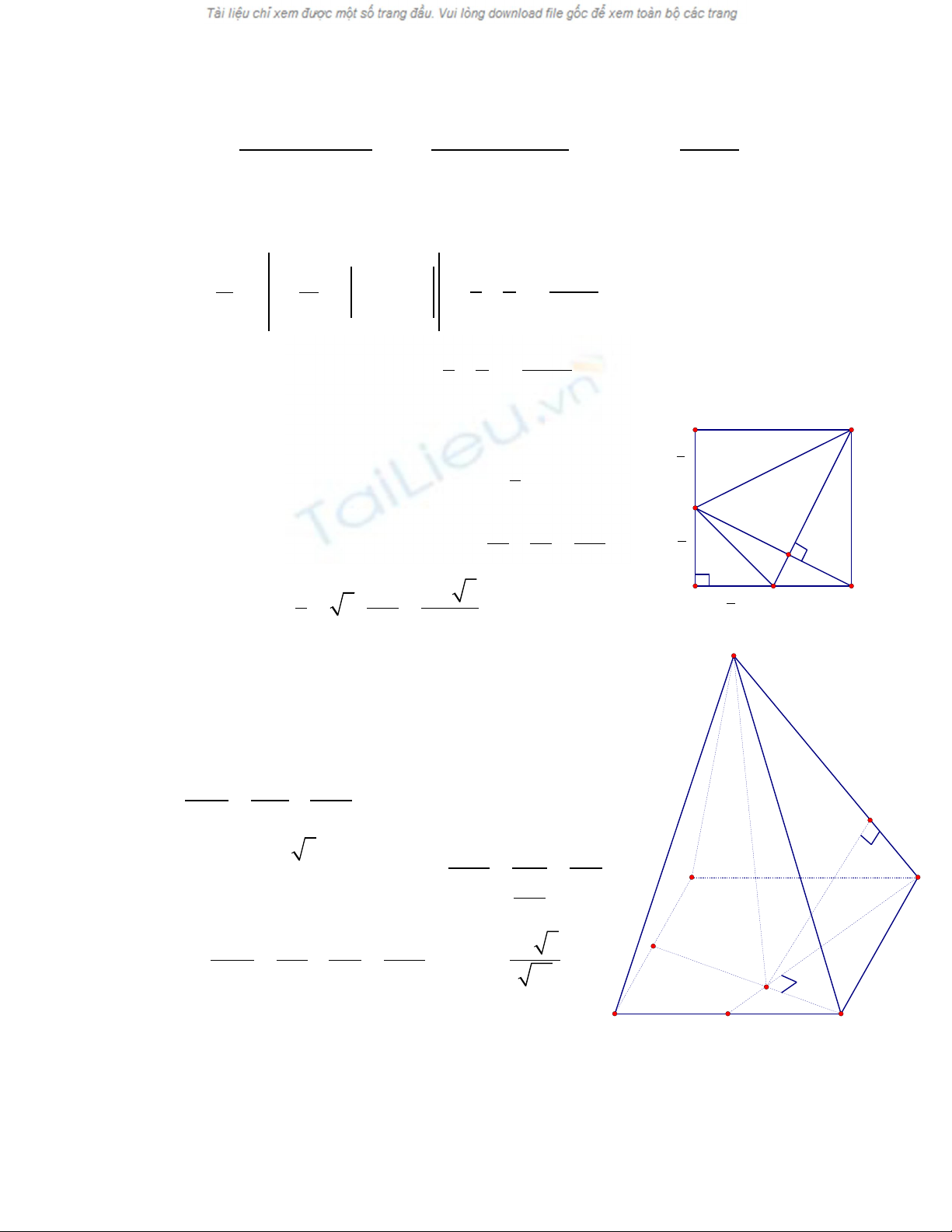
H
M
N
D
B
A
C
S
K
( )
2 x x
1 1 1
2 x 2 x x
2
x x x
0 0 0
x 1 2e e
x e 2x e e
I dx dx x dx
1 2e 1 2e 1 2e
+ +
+ +
= = = +
+ + +
∫ ∫ ∫
1 1
0 0
1 1 1 2e
3 x ln
3 2 3
1 1
x ln 1 2e
3 2
+
= + = +
+
V y ậ
1 1 1 2e
I ln
3 2 3
+
= +
Câu IV
+ Ta có: SH ⊥ (ABCD)
S.CMND CMND
1
V SH.S
3
=
2 2 2
2
CMND ABCD CBM AMD
a a 5a
S S S S a 4 8 8
= − − = − − =
2 3
S.CMND
1 5a a 5 3
V a 3
3 8 24
⇒ = ⋅ ⋅ =
(đvtt)
+ Ta có : ∆CDN = ∆DAM
CN DM DM (SCN) DM SC
SH DM
⊥
⇒ ⇒ ⊥ ⇒ ⊥
⊥
K HK ẻ⊥ SC HK ⊥ MD HK = d(DM, SC)
2 2 2
1 1 1
HK SH HC
= +
v i ớ
4 4 2
2
2
2
2
SH a 3 CD a 4a
CH 5a
CN 5
CN.CH CD
4
=
→ = = =
=
2 2 2 2
1 1 5 19 2a 3
HK
HK 3a 4a 12a 19
⇒ = + = ⇒ =
.
Câu V
a
2
a
2
2
a
a
H
N
M
D
C
B
A
( )
( )
( )
( )
+ + − − = + = − −
⇔
+ + − = + + − =
2 2
2 2 2 2
4x 1 x y 3 5 2y 0 4x 1 x 3 y 5 2y (1)
4x y 2 3 4x 7 4x y 2 3 4x 7 (2)
+ Đi u ki n: ề ệ
≤
≤
3
x4
5
y2
( )
= + ≤ = − − ≤
⇒ ⇒ ⇒ ≥
≥≥
3
(1) (1)
(1)
39 39
VT 4x x VP 3 y 5 2y
(1) y 0
16 16
VP 0 x 0
Suy ra
≤ ≤
≤ ≤
3
0 x 4
5
0 y 2
+ Xét
( )
= +
2
1
f (x) 4x 1 x
tăng trên
3
0 ; 4
,
=
1
f 1
2
( )
= − −
1
g (y) 3 y 5 2y
gi m trên ả
5
0 ; 2
,
( )
=
g 2 1
+
= + −
2
2
f (x) 4x 2 3 4x
gi m trên ả
3
0 ; 4
=
2
2
g (y) y
tăng trên
5
0 ; 2
+ V i ớ
≤ ≤ 1
0 x 2
:
⇒ = < ⇒ >
1 1
(1) g (y) f (x) 1 y 2
> =
⇒
> =
2 2
2 2
1
f (x) f 3
2
g (y) g (2) 4
⇒ >
(2) (2)
VT VP