Nguy n Tu n C ng Tr ng THCS Thái S n – An Lão - H iễ ấ ườ ườ ơ ả
Phòng
Đ C NG ÔN THI VÀO L P 10Ề ƯƠ Ớ
(T ng s 42 ti t)ổ ố ế
===========================================
I. VÒNG 1: ( 18 TI T): NH NG N I DUNG KI N TH C C B NẾ Ữ Ộ Ế Ứ Ơ Ả
A.Đ i s :ạ ố
I.Căn b c hai: Khái ni m, h ng đ ng th c, ĐKXĐ, các phép bi n đ i. (2 ti t ). ậ ệ ằ ẳ ứ ế ổ ế
II.Ph ng trình, b t ph/trình, h ph/ trình b c nh t m t n: D ng, ph/pháp gi i. (2ươ ấ ệ ậ ấ ộ ẩ ạ ả
ti t ).ế
III.Hàm s b c nh t, b c hai: Đ/n, t/c, đ th , t ng giao gi a các đ th . (2 ti t ).ố ậ ấ ậ ồ ị ươ ữ ồ ị ế
IV.Gi i bài toán b ng cách l p h ph ng trình, ph ng trình. (2 ti t ).ả ằ ậ ệ ươ ươ ế
V.Ph ng trình b c hai: D ng, công th c nghi m, Đ nh lý Viet, ng d ng. (2 ti t ).ươ ậ ạ ứ ệ ị ứ ụ ế
B.Hình h c:ọ
I. H th c l ng trong tam giác vuông. T s l ng giác c a góc nh n. (2 ti t ).ệ ứ ượ ỉ ố ượ ủ ọ ế
II. Ch ng minh B ng nhau – Song song; vuông góc - Đ ng quy; th ng hàng. (2 ti t ). ứ ằ ồ ẳ ế
III.Ch ng minh hai tam giác đ ng d ng . H th c hình h c. (2 ti t ).ứ ồ ạ ệ ứ ọ ế
IV.T giác n i ti p: Khái ni m, tính ch t, d u hi u. (2 ti t ).ứ ộ ế ệ ấ ấ ệ ế
II. VÒNG 2: ( 12 TI T): NH NG CHUYÊN Đ CHUYÊN SÂUẾ Ữ Ề
I.C c tr đ i s . (2 ti t ).ự ị ạ ố ế
II. S t ng giao c a các đ ng th ng và parabol trên m t ph ng to đ . (2 ti t ).ự ươ ủ ườ ẳ ặ ẳ ạ ộ ế
III. H th c Vi-et và ng d ng. (2 ti t ).ệ ứ ứ ụ ế
IV. C c tr hình h c. (2 ti t ) ự ị ọ ế
V. Ph ng trình vô t . (2 ti t ).ươ ỉ ế
VI. B t đ ng th c. (2 ti t ). ấ ẳ ứ ế
III. VÒNG 2: ( 12 TI T): THAM KH O M T S Đ THI VÀO THPT Ế Ả Ộ Ố Ề
I. Đ s 1: ề ố
II. Đ s 2:ề ố
III. Đ s 3: ề ố
IV. Đ s 4:ề ố
________________________________________________________
1
Nguy n Tu n C ng Tr ng THCS Thái S n – An Lão - H iễ ấ ườ ườ ơ ả
Phòng
VÒNG 1: ( 18 TI T)Ế
NH NG N I DUNG KI N TH C C B NỮ Ộ Ế Ứ Ơ Ả
§1.CĂN B C HAIẬ
A.KI N TH C C B NẾ Ứ Ơ Ả
1.Khái ni mệ
x là căn b c hai c a s không âm a ậ ủ ố
x2 = a. Kí hi u: ệ
x a=
.
2.Đi u ki n xác đ nh c a bi u th c ề ệ ị ủ ể ứ
A
Bi u th c ể ứ
A
xác đ nh ị
A 0
.
3.H ng đ ng th c căn b c haiằ ẳ ứ ậ
2
A khi A 0
A A A khi A 0
= = − <
4.Các phép bi n đ i căn th cế ổ ứ
+)
( )
A.B A. B A 0; B 0=
+)
( )
A A A 0; B 0
BB
= >
+)
( )
2
A B A B B 0=
+)
+)
( )
( )
2
2
m. A B
mB 0; A B
A B
A B =
−
m
+)
( )
( )
n. A B
nA 0; B 0; A B
A B
A B =
−
m
+)
( )
2
A 2 B m 2 m.n n m n m n = + = =
v i ớ
m n A
m.n B
+ =
=
B.M T S VÍ DỘ Ố Ụ
VD1.Thu g n, tính giá tr các bi u th cọ ị ể ứ
2
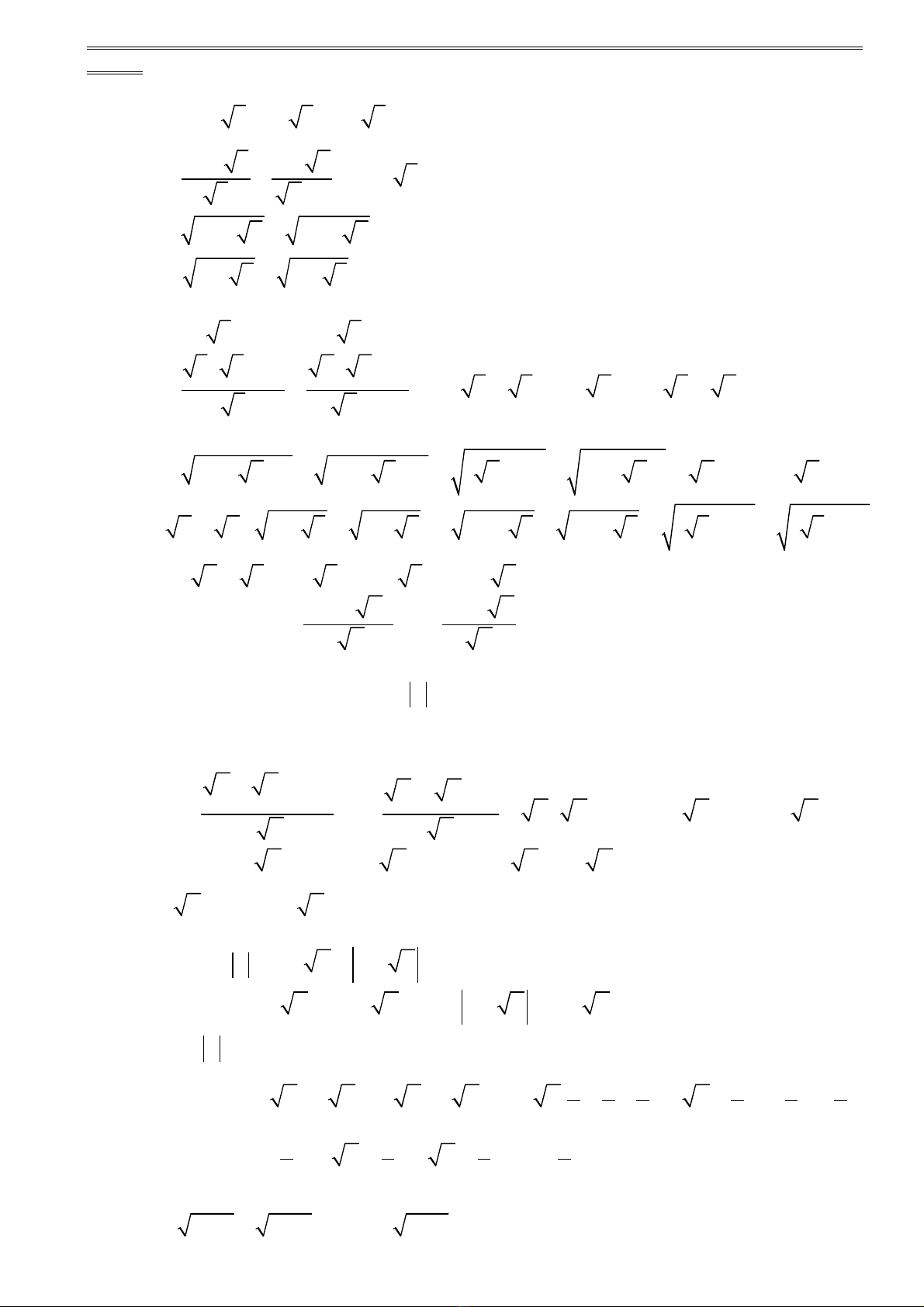
Nguy n Tu n C ng Tr ng THCS Thái S n – An Lão - H iễ ấ ườ ườ ơ ả
Phòng
( ) ( ) ( )
( )
2
A 3 3 2 3 3 3 1
3 2 3 2 2
B 2 3
3 2 1
C 3 2 2 6 4 2
D 2 3 2 3
= − − + +
+ +
= + − +
+
= − − +
= + + −
Gi iả
A 6 3 6 27 6 3 1 34= − + + + + =
( ) ( )
3 3 2 2 2 1
B 2 3 3 2 2 2 3 2
3 2 1
+ +
= + − − = + + − − =
+
( ) ( )
2 2
C 2 2 2 1 4 2 8 2 2 1 2 2 2 1 2 2 1= − + − + + = + − + = + − − = −
()
( ) ( )
2 2
D. 2 2. 2 3 2 3 4 2 3 4 2 3 3 1 3 1
D. 2 3 1 3 1 2 3 D 6
= + + − = + + − = + + −
= + + − = =� �
VD2.Cho bi u th c ể ứ
2
x x 2x x
y 1
x x 1 x
+ +
= + −
− +
a)Rút g n y. Tìm x đ y = 2.ọ ể
b)Cho x > 1. Ch ng minh ứ
yy0− =
c)Tìm giá tr nh nh t c a yị ỏ ấ ủ
Gi iả
a)
( ) ( ) ( )
3
x x 1 x 2 x 1
y 1 x x 1 1 2 x 1 x x
x x 1 x
� �
++
� �
� �
= + − = + + − − = −
− +
( ) ( )
y 2 x x 2 x x 2 0 x 1 x 2 0
x 2 0 x 2 x 4
= − = − − = + − =� � �
− = = =� � �
( đây ta có th áp d ng gi i ph ng trình b c hai b ng cách đ t n ph )Ở ể ụ ả ươ ậ ằ ặ ẩ ụ
b) Có
y y x x x x− = − − −
Do x 1 x x x x 0 x x x x
y y 0
> > − > − = −� � �
− =�
c) Có:
( ) ( )
2
2 2
1 1 1 1 1 1
y x x x x x 2. x. x
2 4 4 2 4 4
� �
= − = − = − + − = + − −
� �
� �
V y ậ
1 1 1 1
Min y khi x x x
4 2 2 4
= − = = =� �
VD3.So sánh hai s sauố
a 1997 1999= +
và
b 2 1998=
Gi iả
3
Nguy n Tu n C ng Tr ng THCS Thái S n – An Lão - H iễ ấ ườ ườ ơ ả
Phòng
Có
( )
2
2 2
a 1998 1 1998 1 1998 1 1998 1
2.1998 2 1998 1 2.1998 2 1998 2 1998
= − + + = − + +
= + − < + =
V y a < b.ậ
C.M T S BÀI T P C B NỘ Ố Ậ Ơ Ả
1.Th c hi n phép tính, rút g n bi u th cự ệ ọ ể ứ
A 4 3 2 2 57 40 2= + − +
B 1100 7 44 2 176 1331= − + −
( )
2
C 1 2002 . 2003 2 2002= − +
1 2
D 72 5 4,5 2 2 27
3 3
= − + +
( )
3 2 3 2
E 6 2 4 . 3 12 6 . 2
2 3 2 3
� �� �
= + − − − −
� �� �
� �� �
F 8 2 15 8 2 15= − − +
G 4 7 4 7= + − −
H 8 60 45 12= + + −
I 9 4 5 9 4 5= − − +
( ) ( )
K 2 8 3 5 7 2 . 72 5 20 2 2= + − − −
2 5 14
L12
+ −
=
( ) ( )
5 3 50 5 24
M75 5 2
+ −
=−
3 5 3 5
N3 5 3 5
+ −
= +
− +
3 8 2 12 20
P3 18 2 27 45
− +
=− +
( )
2
2
1 5 2 5
Q2 5
2 3
� �
−
= − � �
−
� �
+
R 3 13 48= + +
2.Tính giá tr c a bi u th cị ủ ể ứ
1 1 1 1
A khi a ; b
a 1 b 1 7 4 3 7 4 3
= − = =
+ + + −
4
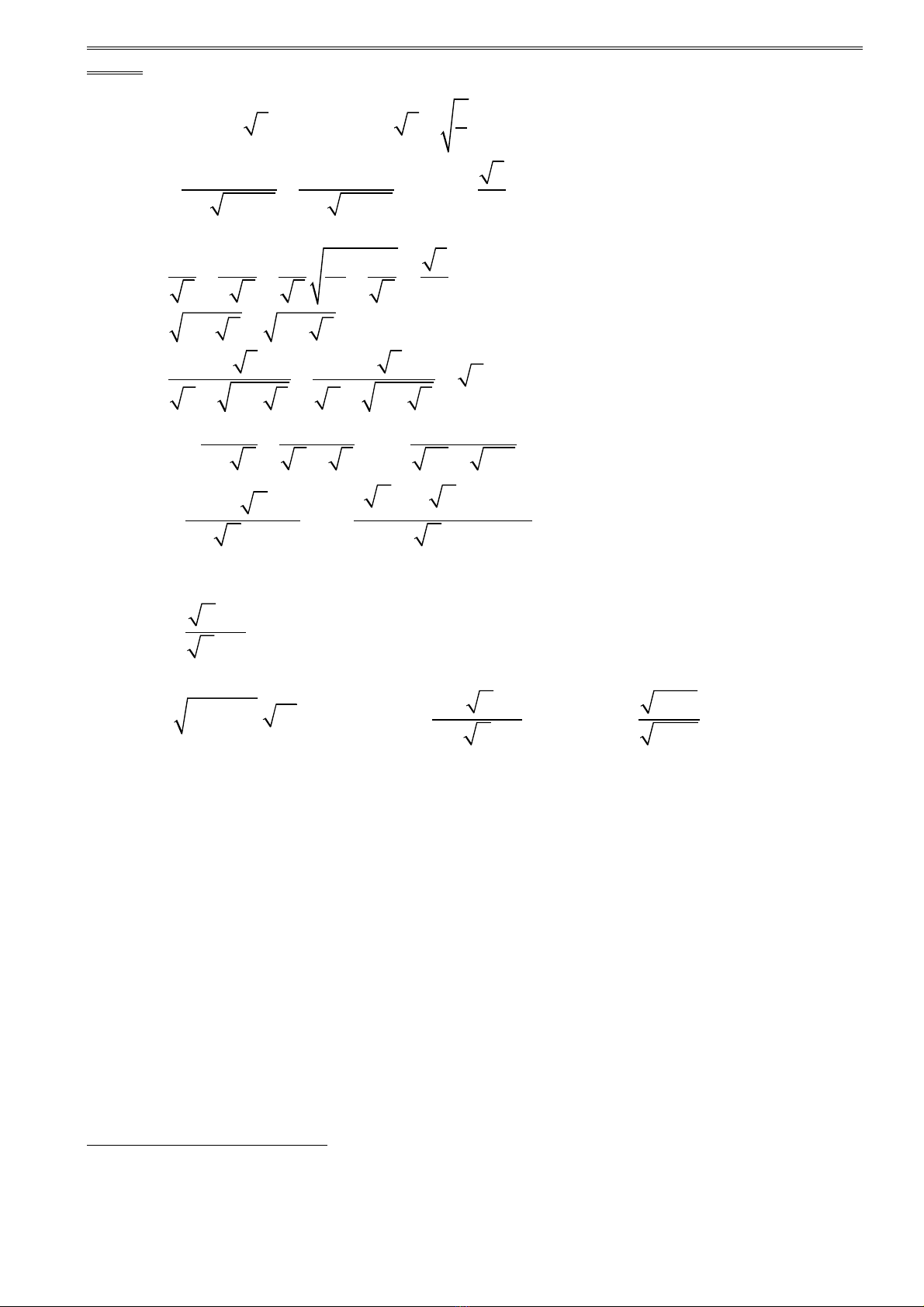
Nguy n Tu n C ng Tr ng THCS Thái S n – An Lão - H iễ ấ ườ ườ ơ ả
Phòng
2
1
B 5x 4 5x 4 khi x 5 5
= − + = +
1 2x 1 2x 3
C khi x 4
1 1 2x 1 1 2x
+ −
= + =
+ + − −
3.Ch ng minhứ
a)
1 1 1 5 1 3
12 2
3 3 2 3 6
+ + − =
b)
3 3
2 5 2 5 1+ + − =
c)
2 3 2 3 2
2 2 3 2 2 3
+ −
+ =
+ + − −
d)
1 1 1
S ...
1 2 2 3 99 100
= + + +
+ + +
là m t s nguyên.ộ ố
4.Cho
( )
3
x x 2x 2
2x 3 x 2
A ; B
x 2 x 2
− + −
− −
= =
− +
a) Rút g n A và B.ọ
b) Tìm x đ A = B.ể
5.Cho
x 1
Ax 3
+
=−
. Tìm s nguyên x đ A nh n giá tr nguyên.ố ể ậ ị
6.Tìm x, bi t:ế
( )
2
x x 1 x 5
a) 4 x . 81 36 b) 3 c) 1
x x 4
+ + −
− = = =
−
________________________________________________
§2.H TH C L NG TRONG TAM GIÁC VUÔNGỆ Ứ ƯỢ
T S L NG GIÁC C A GÓC NH NỈ Ố ƯỢ Ủ Ọ
A.KI N TH C C B NẾ Ứ Ơ Ả
1.Đ nh lý Pitagoị
ABC∆
vuông t i A ạ
222
AB AC BC+ =�
2.H th c l ng trong tam giác vuôngệ ứ ượ
5