ĐỀ ÔN TẬP SỐ 2 THI ĐẠI HỌC, CAO ĐẲNG
Môn thi: TOÁN, khối B
Thời gian làm bài 180 phút, không kể thời gian phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I (2 điểm) Cho hàm số
2(3 2) 1 2
(1)
2
x m x m
y
x
, với m là tham số thực. 1.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.
2. Tìm các giá trị của m để hàm số (1) đồng biến trên từng khoảng xác định của nó.
Câu II (2 điểm) 1. Giải phương trình 2
3sin cos2 sin2x =4sinxcos .
2
x
x x
2. Giải hệ phương trình 3
4
1 8
( , ).
( 4)
x y x
x y R
x y
Câu III (2 điểm)Trong không gian với hệ tọa độ Oxyz cho ba điểm
A(1; 0; -1), B(2; 3; -1), C(1; 3; 1) và đường thẳng d: 1 0
x y
x y z
1. Tìm tọa độ điểm D thuộc đường thẳng d sao cho thể tích của khối tứ diện ABCD
bằng 1.
2. Viết phương trình tham số của đường thẳng đi qua trực tâm H của tam giác ABC
và vuông góc với mặt phẳng (ABC).
Câu IV (2 điểm) 1. Tính tích phân
13
2
0
.
4
x dx
I
x
2. Cho số nguyên n (n ≥ 2) và hai số thực không âm x, y. Chứng minh rằng
1 1
1
.
n n n n
n n
x y x y
Đẳng thức xảy ra khi nào?
PHẦN RIÊNG : Thí sinh chỉ được làm 1 trong 2 câu: V.a hoặc V.b.
Câu V.a. Theo chương trình KHÔNG phân ban (2 điểm)
1. Chứng minh rằng
0 1 1 1 1 0 1
2 2 2 2
3 1
...
1 2 1 2( 1)
n n n n n
n n n n
C C C C
n n n
(n là số nguyên dương,
k
n
C
là số tổ hợp chập k của n phần tử).
2. Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(3; 0), B(0; 4). Chứng minh
rằng đường tròn nội tiếp tam giác OAB tiếp xúc với đường tròn đi qua trung điểm
các cạnh của tam giác OAB.
Câu V.b. Theo chương trình phân ban (2 điểm)
1. Giải bất phương trình 2 1 2 1
3 2 5.6 0.
x x x
2. Cho tứ diện ABCD có các mặt ABC và ABD là các tam giác đều cạnh a, các mặt
ACD và BCD vuông góc với nhau. Hãy tính theo a thể tích khối tứ diện ABCD và
tính số đo của góc giữa hai đường thẳng AD, BC.
ĐÁP ÁN – THANG ĐIỂM
Môn: TOÁN (đề số 2), khối B
Câu
Nội dung Điểm
I 2,00
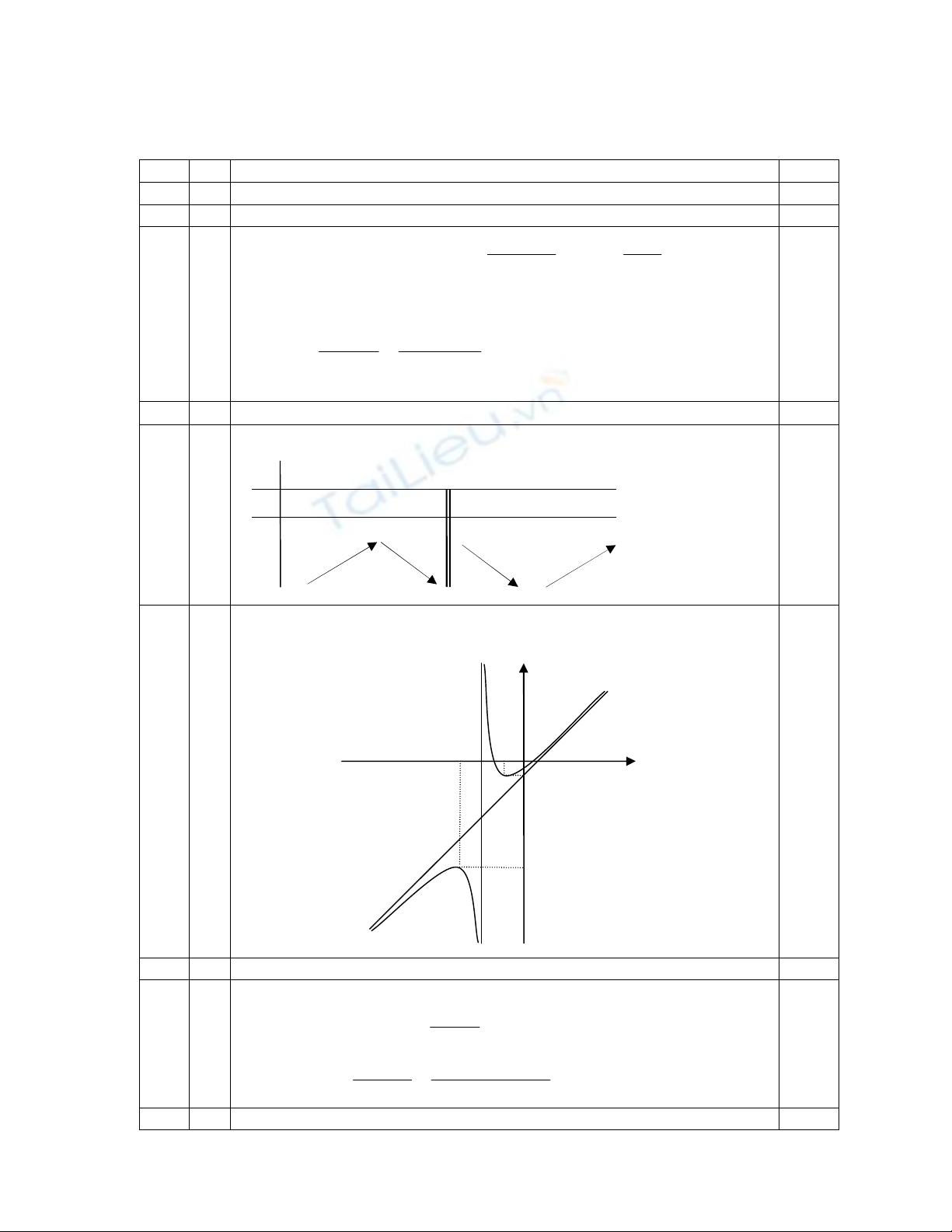
1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1,00 điểm)
Khi m = 1 hàm số trở thành 2
1 1
1 .
2 2
x x
y x
x x
Tập xác định : R \ {-2}.
Sự biến thiên:
2
' '
2 2
1 4 3
1 , 0 3 1.
( 2) ( 2)
x x
y y x hay x
x x
yCĐ = y(-3) = -5, yCT = y(-1) = -1.
0,25
Tiệm cận: Tiệm cận đứng x = -2, tiệm cận xiên y = x – 1. 0,25
Bảng biến thiên:
0,25
Đồ thị:
0,25
2 Tìm các giá trị của m…(1,00 điểm)
Ta có
2
'
2 2
9 8
(3 4) .
2
8 9 4 8 5
1 .
( 2) ( 2)
m
y x m x
m x x m
yx x
0,50
Hàm số đã cho đồng biến trên các khoảng xác định của nó khi và chỉ
x
'
y
y


+ +




2
3
0
5
1
0
1
0
y
x
-5
-1
-3
-2
-1
khi ' 2
9
0 2 4 8 5 0 2 .
8
y x x x m x m
0,50
II 2,00
1 Giải phương trình lượng giác (1,00 điểm)
Phương trình đã cho tương đương với 2
3sin cos2 sin2x=2sinx+sin2x 2sin sin 1 0
(sin 1)(2sin 1) 0.
x x x x
x x
0,50
sin 1 2 .
2
x x k
1
sin 2
2 6
x x k
hoặc 7
2 .
6
x k
Nghiệm của phương trình là 7
2 2 2 , .
2 6 6
x k x k x k k
Z
0,50
2 Giải hệ phương trình (1,00 điểm)
Điều kiện
0, 0
x y
. Hệ phương trình đã cho tương đương với
2 3
4
1 ( 1) 8 0 (1)
( 1) (2)
x x x
y x
Xét hàm số 2 3
( ) 1 ( 1) 8
f t t t t
, với t ≥ 1.
Ta có / 2 2 1
( ) ( 1) 2 1 0
2 1
f t t t t
với mọi t > 1 nên f(t) đồng
biến trên (1; +∞).
0,50
Phương trình (1) có dạng f(x) = f(2) nên (1) x = 2, thay vào (2) ta
được y = 1.
Nghiệm của hệ phương trình là (x; y) = (2; 1).
0,50
III
1 Tìm tọa độ điểm D…(1,00 điểm)
Ta có vectơ
AB
= (1; 3; 0), vectơ
AC

= (0; 3; 2). Suy ra tích có
hướng của hai vectơ AB, AC là vectơ
n
= (6; -2; 3).
Phương trình của đường thẳng d là : 1
3 2 .
x t
y t
z t
Vì D d nên D(t; 1 + t; 3 – 2t)
( 1; 1; 2 4).
AD t t t
2
1 1
. 6( 1) 2( 1) 3( 2 4) .
6 6 3
ABCD
t
V n AD t t t
0,50
Do đó 2
1 1 1 5.
3
ABCD
t
V t hay t
Có hai điểm D thỏa mãn bài toán là: D( - 1 ; 0 ; 5) và D(5 ; 6 ; -7).
0,50
2 Viết phương trình tham số của đường thẳng (1,00 điểm)
Phương trình mặt phẳng () qua C và vuông góc với AB là:
1(x - 1) + 3(y - 3) = 0 x + 3y – 10 = 0.
0,50
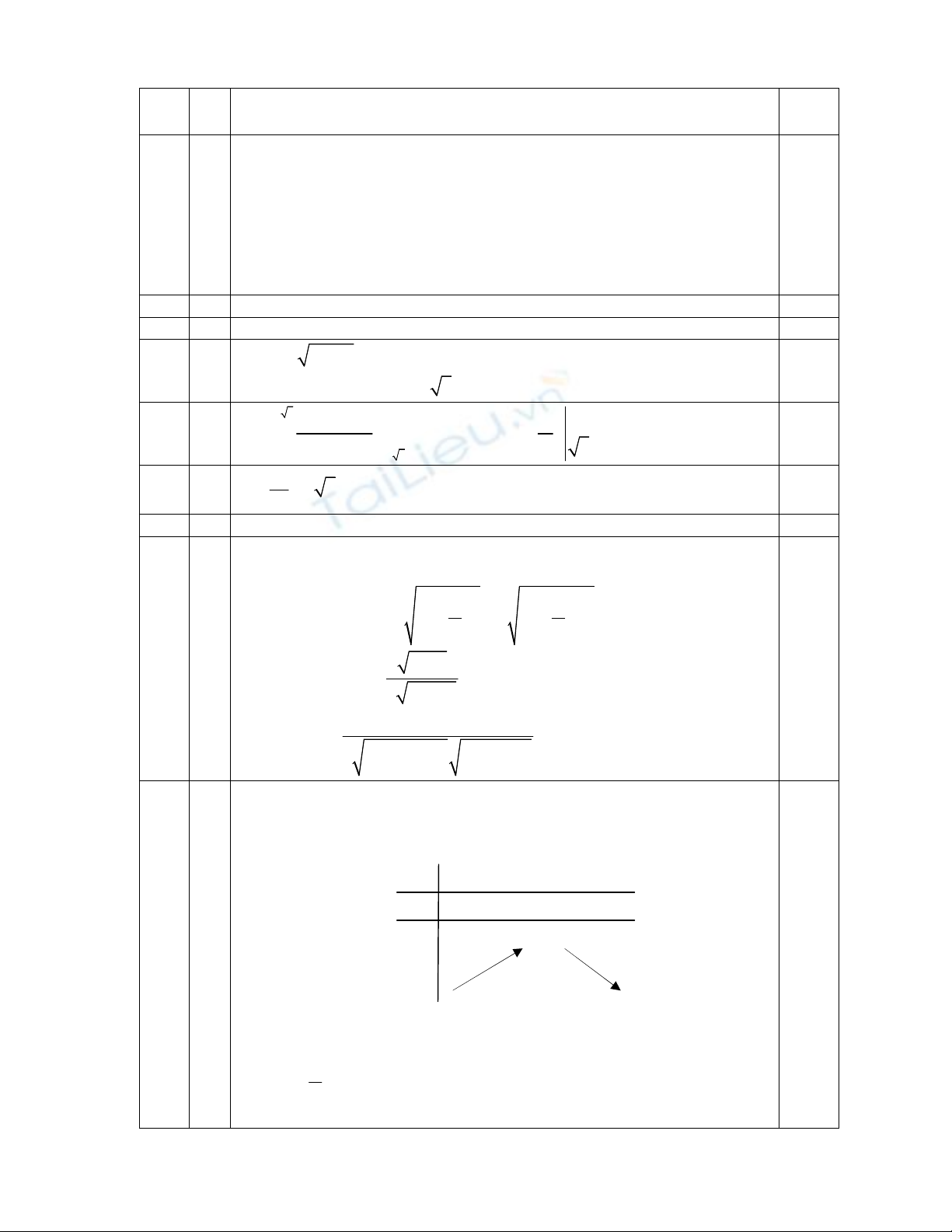
Phương trình mặt phẳng () qua B và vuông góc với AC là:
3(y - 3) + 2(z + 1) = 0 3y + 2z – 7 = 0.
Gọi là đường thẳng qua trực tâm H của tam giác ABC và vuông góc
với mặt phẳng (ABC), suy ra là giao tuyến của () và ().
Nhận thấy N(1;3;-1)
và
nhận
n
làm một vectơ chỉ phương nên
phương trình tham số là:
1 6
3 2
1 3 .
x t
y t
z t
0,50
IV 2,00
1 Tính tích phân … (1,00 điểm)
Đặt 2 2 2
4 4 , .
t x x t xdx tdt
0 2, 1 3
x t x t
0,25
3 2
2 3
2
23
2
(4 ) (4 ) 4 3
3
t tdt t
I t dt t
t
0,50
16
3 3
3
. 0,25
2 Chứng minh bất đẳng thức (1,00 điểm)
Với x = 0 hoặc y = 0, bất đẳng thức đúng và dấu bằng xảy ra.
Với xy 0, bất đẳng thức cần chứng minh tương đương với
1
1
1 1
n n
n n
x x
y y
.
Xét hàm số
1 1
1
( ) 1
n n
n n
t
f t
t
với
(0; )
t
.
Ta có
1
' '
2 1
1
1
(1 )
( ) , ( ) 0 1
1 1
n
n n
n n
n n
t t
f t f t t
t t
.
0,50
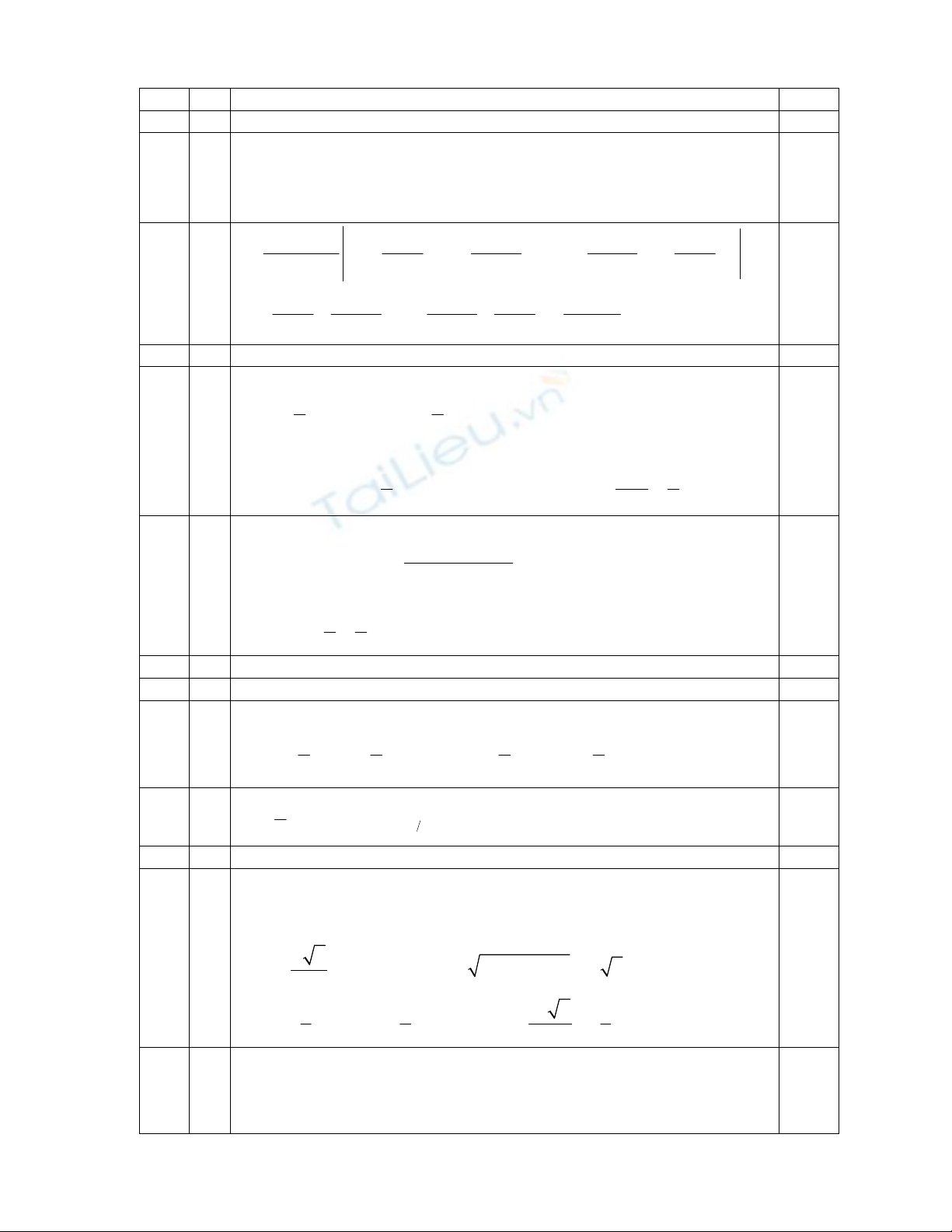
0
lim ( ) 1, lim ( ) 1
t
tf t f t

.
Bảng biến thiên:
Từ bảng biến thiên suy ra f(t) ≥ 1 với mọi
(0; )
t
.
Thay
y
t
x
ta được điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi x = 0 hoặc y = 0.
0,50
x
'
( )
f t
( )
f t
0
0

+
1
1
1
0
(1)
f
V.a 2,00
1 Chứng minh đẳng thức tổ hợp (1,00 điểm)
Xét khai triển 0 1 1 1
(2 1) (2 ) (2 ) ... (2 ) .
n n n n n
n n n n
x C x C x C x C
Suy ra 1 1 0 1 1 1
0 0
(2 1) [ (2 ) (2 ) ... (2 ) ] .
n n n n n
n n n n
x dx C x C x C x C dx
0,50
0 1 1 1 1 01 1 2
1 1
2 2 2 2(2 1) ...
0 0
2( 1) 1 2 1
n n n nn n n
n n n n
C C C Cx
x x x x
n n n
0 1 1 1 1 0 1
2 2 2 2
3 1
... .
1 2 1 2( 1)
n n n n n
n n n n
C C C C
n n n
0,50
2 Chứng minh hai đường tròn tiếp xúc với nhau (1,00 điểm)
Gọi M, N, P lần lượt là trung điểm của OA, OB, AB.
3 3
;0 , 0;2 , ;2 .
2 2
M N P
Tam giác MNP vuông tại P nên tâm đường tròn đi qua ba điểm M, N,
P là trung điểm
3
;1
4
I
của MN và bán kính
5
.
2 4
MN
R
0,50
Mặt khác tam giác OAB vuông tại O nên đường tròn nội tiếp tam giác
OAB có bán kính
1
2
OA OB AB
r
và tâm J nằm trên đường
thẳng y = x và thuộc góc phần tư thứ nhất nên J(1; 1).
Ta có 1 5
1 ,
4 4
IJ R r
suy ra điều phải chứng minh.
0,50
V.b 2,00
1 Giải bất phương trình logarit (1,00 điểm)
Bất phương trình đã cho tương đương với
2
3 3 3 3
3 5 2 0 2 3 1 0
2 2 2 2
x x x x
0,50
3 2
3
2 log 2.
2
x
x
0,50
2 Tính thể tích và góc (1,00 điểm)
Gọi M là trung điểm của CD, khi đó AM CD, BM CD. Từ giả
thiết suy ra
90
AMB
. Mà AM = BM nên AMB vuông cân tại M.
Do đó
2 2
3
22 2 2
2
1 1 2 1
. . . .( . )
3 6 12 3
ABCD ABM BCD
a
BM CD CM BC BM a
a
V CD S CD AM BM AM S
0,50
Gọi N, P,Q lần lượt là trung điểm của AB, AC, BD.
Ta có
, ,
AD BC NP NQ
.