Trang 1/41 - Mã đề 001
TRƯỜNG THPT THANH MIỆN
TỔ TOÁN
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2019 - 2020
Môn: TOÁN - Lớp 10 - Chương trình chuẩn
ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
001
Câu 1. Cho hàm số
2
y ax bx c
, với
0a
, có đồ thị
P
. Khi đó, tọa độ đỉnh của
P
là
A.
. B.
;
24
b
Iaa



. C.
;
b
Iaa




. D.
;
24
b
Iaa




.
Câu 2. Khẳng định nào sau đây là sai?
A.
ka
và
a
cùng hướng khi
0k
.
B.
ka
và
a
cùng hướng khi
0k
.
C. Hai vectơ
a
và
0b
cùng phương khi có một số
k
để
a kb
.
D.
1.aa
.
Câu 3. Cho tam giác
ABC
có trọng tâm là
G
. Phát biểu nào sau đây là đúng?
A.
0GA GB GC
. B.
0GA GB GC
.
C.
AB BC AC
. D.
AB BC AC
.
Câu 4. Trong hệ tọa độ
Oxy
, cho
1;3a
,
2;1b
. Tích vô hướng của hai vector
.ab
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 5. Trong hệ tọa độ
Oxy
, cho
2;7a
,
3;5b
. Tọa độ của vector
ab
là
A.
5; 2
. B.
1;2
. C.
5; 2
. D.
5;2
.
Câu 6. Hãy liệt kê các phần tử của tập hợp
2
/ 1 0X x x x
.
A.
0X
. B.
X
. C.
X
. D.
0X
.
Câu 7. Phương trình nào sau đây nhận
2x
và
7x
làm nghiệm.
A.
29 14 0xx
. B.
29 14 0xx
. C.
29 14 0xx
. D.
29 14 0xx
.
Câu 8. Phương trình
20ax bx c
có nghiệm duy nhất khi và chỉ khi
A.
0
0
a

hoặc
0
0
a
b
. B.
0abc
.
C.
0
0
a

. D.
0a
.
Câu 9. Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn?
A.
31
22
xy
xy


. B.
2
1
0
x y z
xy

. C.
2
2
51
0
xy
xy


. D.
210
10
xx
x

.
Câu 10. Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
2y
. B.
3yx
. C.
23yx
. D.
2yx

.
Câu 11. Cho tập
2,3,4X
. Hỏi tập
X
có bao nhiêu tập hợp con?
A.
6
. B.
5
. C.
8
. D.
7
.
Câu 12. Cho
2
: 2 3P y x x
. Tìm mệnh đề đúng.
A. Hàm số nghịch biến trên
;1
. B. Hàm số đồng biến trên
;2
.
C. Hàm số nghịch biến trên
;2
. D. Hàm số đồng biến trên
;1
.
Câu 13. Giải phương trình
267x x x
ta được nghiệm là
A.
4x
. B.
5x
. C.
11
3
x
. D.
3x
.
Câu 14. Nếu
tan 3
thì
cos
bằng bao nhiêu?
A.
1
3
. B.
10
10
. C.
10
10
. D.
10
10
.
Câu 15. Cho tam giác
ABC
có
60 , 5, 8.A AB AC
Tính
.AB AC
.
A.
13
. B.
60
. C.
44
. D.
20
.
Câu 16. Cho hàm số
3
y x x
, mệnh đề nào sau đây đúng?
A. Hàm số đã cho là hàm số lẻ.
B. Hàm số đã cho là hàm số chẵn.
C. Hàm số đã cho không là hàm số chẵn, không là hàm số lẻ.
D. Hàm số đã cho vừa là hàm số chẵn, vừa là hàm số lẻ.
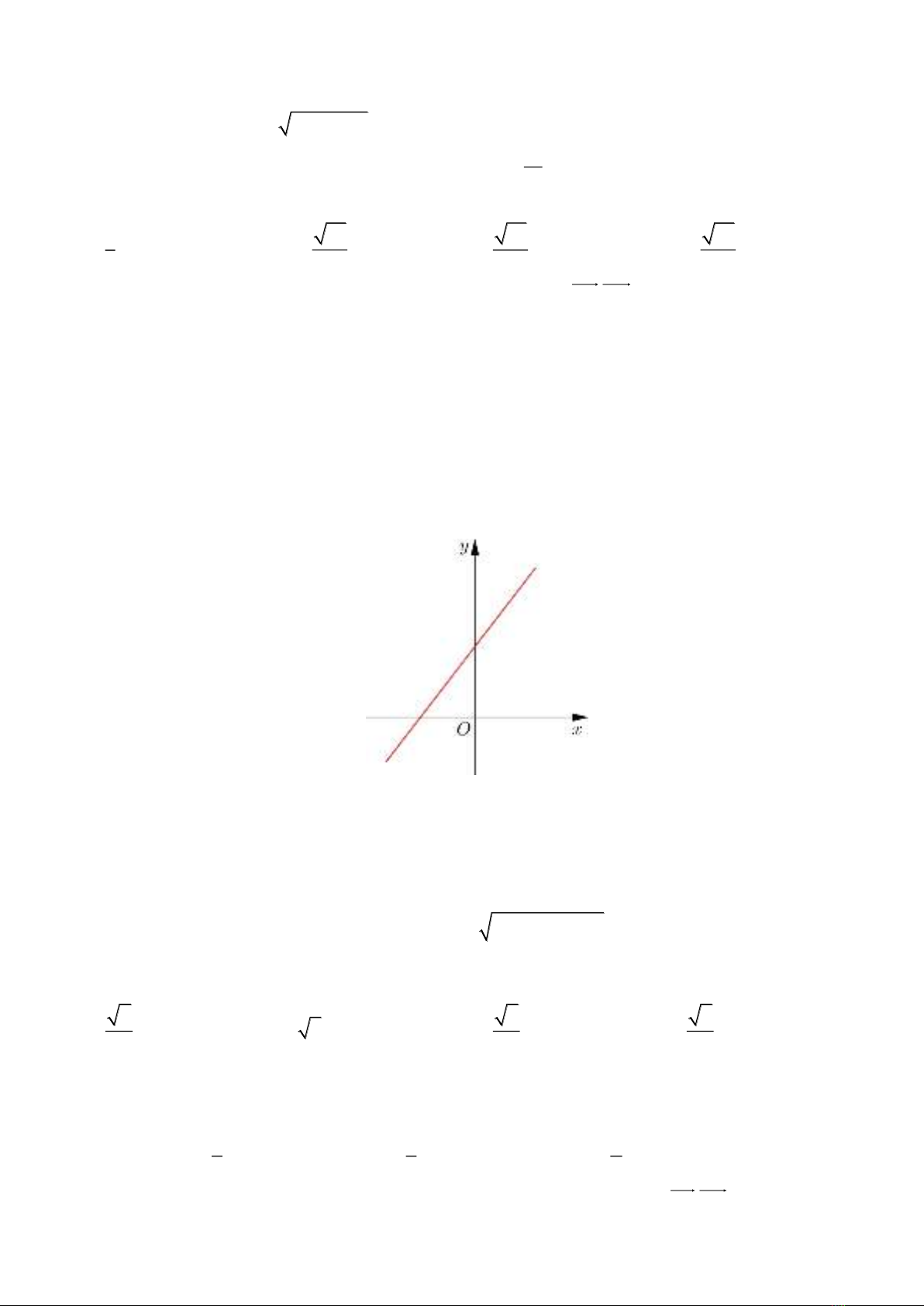
Câu 17. Cho hàm số
y ax b
có đồ thị như hình vẽ sau
Khẳng định nào sau đây đúng?
A.
0a
,
0b
. B.
0a
,
0b
. C.
0a
,
0b
. D.
0a
,
0b
.
Câu 18. Tìm tất cả giá trị thực của tham số
m
để phương trình
2 4 2m x m
có nghiệm duy
nhất.
A.
2m
. B.
2m
. C.
1m
. D.
1m
.
Câu 19. Số nghiệm của phương trình
22 8 4 4 2x x x x
là
A. 4. B. 2. C. 1. D. 3.
Câu 20. Tam giác
ABC
có
75A
,
45B
,
2AC
. Tính độ dài của cạnh
AB
.
A.
2
2
. B.
6
. C.
6
2
. D.
6
3
.
Câu 21. Biết rằng phương trình
2
1 1 0m x m x m
có một nghiệm là
12x
, tìm
m
và
nghiệm
2
x
còn lại.
A.
2
3
3, 8
mx
. B.
2
1
2, 3
mx
. C.
2
3
3, 4
mx
D.
2
2, 1mx
.
Câu 22. Tam giác
ABC
vuông ở
A
,
AB c
,
AC b
. Tính tích vô hướng
.BA BC
theo
,bc
.
A.
2
c
. B.
22
bc
. C.
2
b
. D.
22
bc
.
Câu 23. Phương trình của đường thẳng có hệ số góc
3a
và đi qua điểm
1;4A
là
A.
33yx
. B.
31yx
. C.
31yx
. D.
34yx
.
Câu 24. Hãy chọn kết quả đúng khi phân tích vectơ
AM
theo hai véctơ
AB
và
AC
của tam giác
ABC
với
M
là trung điểm của đoạn
BC
.
A.
1
3
AM AB AC
. B.
AM AB AC
. C.
23AM AB AC
.
D.
1
2
AM AB AC
.
Câu 25. Xác định
2
:2P y x bx c
, biết
P
có hoành độ đỉnh bằng
3
và đi qua điểm
2; 3A
.
A.
2
: 2 12 19P y x x
. B.
2
: 2 4 9P y x x
.
C.
2
: 2 12 19P y x x
. D.
2
: 2 4 9P y x x
.
Câu 26. Cho
., 3; 2 1;6uv
Khẳng định nào sau đây là đúng?
A.
uv
và
6; 24b
cùng hướng. B.
, uv
cùng phương.
C.
, u v v
cùng phương. D.
uv
và
4;4a
ngược hướng.
Câu 27. Trong hệ tọa độ
Oxy
, cho 2 điểm
()1;2 , 3;1AB
.Tìm tọa độ điểm
C
trên
Oy
sao cho tam
giác
ABC
vuông tại
A
.
A.
(0; )6
. B.
3;1
. C.
5;0
. D.
0;6
.
Câu 28. Cho hai điểm
B
,
C
phân biệt. Tập hợp những điểm
M
thỏa mãn
2
.CM CB CM
là
A. đường tròn đường kính
BC
. B. đường tròn tâm
B
, bán kính
BC
.
C. đường tròn tâm
C
, bán kính
BC
. D. đường thẳng vuông góc với
BC
tại
B
.
Câu 29. Cho hàm số
2,0y ax bx c a
có bảng biến thiên như sau
.
Trong bốn parabol dưới đây, parabol nào là đồ thị của hàm số trên?
A. . B. . C. . D. .
Câu 30. Cho phương trình
22
13 2 7 0
4x m x m m
. Tìm
m
để phương trình có hai nghiệm
phân biệt.
A.
1
2
m
. B.
1
2
m
. C.
1
2
m
. D.
1
2
m
.
Câu 31. Hàm số
y x x
được viết theo cách cho hàm số bởi nhiều công thức là
A.
0 khi 0
2 khi 0
x
yxx
. B.
2 khi 0
0 khi 0
xx
yx
.
C.
2 khi 0
0 khi 0
xx
yx

. D.
khi 0
2 khi 0
xx
yxx
.
Câu 32. Gọi
0 0 0
;;x y z
là nghiệm của hệ phương trình
11
25
3 2 24
x y z
x y z
x y z
. Tính giá trị của biểu thức
0 0 0.P x y z
A.
40.P
B.
40.P
C.
1200.P
D.
1200.P
Câu 33. Trong hệ tọa độ
Oxy
, cho 2 vector
(4;5)u
và
(3; )va
. Tìm
a
để
.0uv
.
A.
5
12
a
. B.
5
12
a
. C.
12
5
a
. D.
12
5
a
.
Câu 34. Hàm số nào trong các hàm số sau đây là hàm số lẻ?
A.
2 2 2y x x
. B.
2 2 2y x x
.
C.
22y x x
. D.
22y x x
.
Câu 35. Trong hệ tọa độ
,Oxy
cho tam giác
ABC
có
2; 3 , 0; 4 , 1; 6M N P
lần lượt là
trung điểm của các cạnh
,,BC CA AB
. Tìm tọa độ đỉnh
A
?
A.
2; 7
. B.
1; 10
. C.
1;5
. D.
3; 1
.
Câu 36. Cho ba tập hợp
;2A
,
3;B
và
0;4C
. Khi đó tập
A B C
là
A.
3;4
. B.
; 2 3; 
. C.
3;4
. D.
; 2 3; 
.
Câu 37. Gọi
S
là tập hợp các giá trị thực của tham số
m
sao cho parabol
2
:4P y x x m
cắt
Ox
tại hai điểm phân biệt
, AB
thỏa mãn
3.OA OB
Tính tổng
T
các phần tử của
.S
A.
3.
2
T
B.
3.T
C.
9.T
D.
15.T
Câu 38. Cho hệ phương trình
2 2 2
2
42
xy
x y xy m m

. Tìm tập hợp tất cả các giá trị của
m
để hệ
phương trình trên có nghiệm.
A.
0;2
. B.
1
;2



. C.
1; 
. D.
1;1
2



.
Câu 39. Tổng các nghiệm của phương trình
2
2 2 7 4x x x
bằng
A. 4. B. 1. C. 2. D. 3.
Câu 40. Gọi
12
, xx
là hai nghiệm của phương trình
22
2 2 2 0x mx m
(
m
là tham số). Tìm giá
trị lớn nhất
max
P
của biểu thức
1 2 1 2
2 4 .P x x x x
A.
max
23.
4
P
B.
max 2.P
C.
max
25.
4
P
D.
max
9.
4
P
Câu 41. Trong hệ tọa độ
,Oxy
cho hai điểm
–2;2 , 1;1MN
. Tìm tọa độ điểm
P
trên
Ox
sao cho
ba điểm
,,M N P
thẳng hàng.
A.
–4;0P
. B.
4;0P
. C.
0;4P
. D.
0;–4P
.
Câu 42. Trong hệ tọa độ
,Oxy
cho bốn điểm
2;1A
,
2; 1B
,
2; 3C
,
2; 1D
. Xét ba
mệnh đề:
: I ABCD
là hình thoi;
: II ABCD
là hình bình hành;
: III AC
cắt
BD
tại
0; 1M
.
Chọn khẳng định đúng.
A. Chỉ
II
và
III
đúng. B. Cả ba đều đúng.
C. Chỉ
I
đúng. D. Chỉ
II
đúng.
Câu 43. Phương trình
22
1 . 4 2m x m x m
nghiệm đúng với mọi
x
khi và chỉ khi
A.
0m
hoặc
2m
. B.
m
. C.
0m
. D.
2m
.
Câu 44. Cho số thực
0m
. Tìm điều kiện cần và đủ để hai khoảng
;2m
và
8;
m




có giao
khác tập rỗng.
A.
20m
. B.
2m
. C.
20m
. D.
2m
.
Câu 45. Biết rằng đồ thị hàm số
y ax b
đi qua điểm
2; 1E
và song song với đường thẳng
ON
với
O
là gốc tọa độ và
1;3N
. Tính giá trị biểu thức
22
.S a b

A.
64S
. B.
42S
. C.
58S
. D.
66S
.
Câu 46. Hệ phương trình
2
2
32
32


x x y
y y x
có số nghiệm là
A. 2. B. 3. C. 4. D. 1.
Câu 47. Cho parabol
2
: 4 3P y x x
và đường thẳng
:3d y mx
. Tìm tất cả các giá trị thực
của
m
để
d
cắt
P
tại hai điểm phân biệt
,AB
sao cho diện tích tam giác
OAB
bằng
9
2
.
A.
7m
. B.
1, 7mm
. C.
1m
. D.
7m
.
Câu 48. Số các giá trị nguyên của tham số
2018;2018m
để phương trình
23
2 4 4 4x m x x x
có nghiệm là
A. 2021. B. 2018. C. 2019. D. 2020.
Câu 49. Cho tam giác đều
ABC
cạnh
.a
Biết rằng tập hợp các điểm
M
thỏa mãn đẳng thức
2 3 4MA MB MC MB MA
là đường tròn cố định có bán kính
.R
Tính bán kính
R
theo
.a
A.
.
2
a
R
B.
.
6
a
R
C.
.
3
a
R
D.
.
9
a
R
Câu 50. Cho hai số
, xy
thỏa mãn
22
1x y xy
. Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của
4 4 2 2
P x y x y
. Tính tích
Mm
.
A.
1
6
. B.
1
2
. C.
1
. D.
1
3
.
------------- HẾT -------------