13th International Mathematics Competition for University Students
Odessa, July 20-26, 2006
First Day
Problem 1. Let f:R→Rbe a real function. Prove or disprove each of the following statements.
(a) If fis continuous and range(f) = Rthen fis monotonic.
(b) If fis monotonic and range(f) = Rthen fis continuous.
(c) If fis monotonic and fis continuous then range(f) = R.
(20 points)
Solution. (a) False. Consider function f(x) = x3−x. It is continuous, range(f) = Rbut, for example,
f(0) = 0, f(1
2) = −3
8and f(1) = 0, therefore f(0) > f(1
2), f(1
2)< f(1) and fis not monotonic.
(b) True. Assume first that fis non-decreasing. For an arbitrary number a, the limits lim
a−fand
lim
a+fexist and lim
a−f≤lim
a+f. If the two limits are equal, the function is continuous at a. Otherwise,
if lim
a−f=b < lim
a+f=c, we have f(x)≤bfor all x < a and f(x)≥cfor all x > a; therefore
range(f)⊂(−∞, b)∪(c, ∞)∪ {f(a)}cannot be the complete R.
For non-increasing fthe same can be applied writing reverse relations or g(x) = −f(x).
(c) False. The function g(x) = arctan xis monotonic and continuous, but range(g) = (−π/2, π/2) 6=R.
Problem 2. Find the number of positive integers xsatisfying the following two conditions:
1. x < 102006;
2. x2−xis divisible by 102006.
(20 points)
Solution 1. Let Sk=0< x < 10k
x2−xis divisible by 10kand s(k) = |Sk|, k ≥1.Let x=
ak+1ak. . . a1be the decimal writing of an integer x∈Sk+1, k ≥1.Then obviously y=ak. . . a1∈Sk.Now,
let y=ak. . . a1∈Skbe fixed. Considering ak+1 as a variable digit, we have x2−x=ak+110k+y2−
ak+110k+y= (y2−y) + ak+110k(2y−1) + a2
k+1102k.Since y2−y= 10kzfor an iteger z, it follows that
x2−xis divisible by 10k+1 if and only if z+ak+1 (2y−1) ≡0 (mod 10).Since y≡3 (mod 10) is obviously
impossible, the congruence has exactly one solution. Hence we obtain a one-to-one correspondence between
the sets Sk+1 and Skfor every k≥1.Therefore s(2006) = s(1) = 3,because S1={1,5,6}.
Solution 2. Since x2−x=x(x−1) and the numbers xand x−1 are relatively prime, one of them must
be divisible by 22006 and one of them (may be the same) must be divisible by 52006. Therefore, xmust
satisfy the following two conditions:
x≡0 or 1 (mod 22006);
x≡0 or 1 (mod 52006).
Altogether we have 4 cases. The Chinese remainder theorem yields that in each case there is a unique
solution among the numbers 0,1,...,102006 −1. These four numbers are different because each two gives
different residues modulo 22006 or 52006. Moreover, one of the numbers is 0 which is not allowed.
Therefore there exist 3 solutions.
Problem 3. Let Abe an n×n-matrix with integer entries and b1, . . . , bkbe integers satisfying det A=
b1·...·bk. Prove that there exist n×n-matrices B1, . . . , Bkwith integer entries such that A=B1·. . . ·Bk
and det Bi=bifor all i= 1,...,k.
(20 points)
Solution. By induction, it is enough to consider the case m= 2. Furthermore, we can multiply Awith
any integral matrix with determinant 1 from the right or from the left, without changing the problem.
Hence we can assume Ato be upper triangular.
1
13th International Mathematics Competition for University Students
Odessa, July 20-26, 2006
Second Day
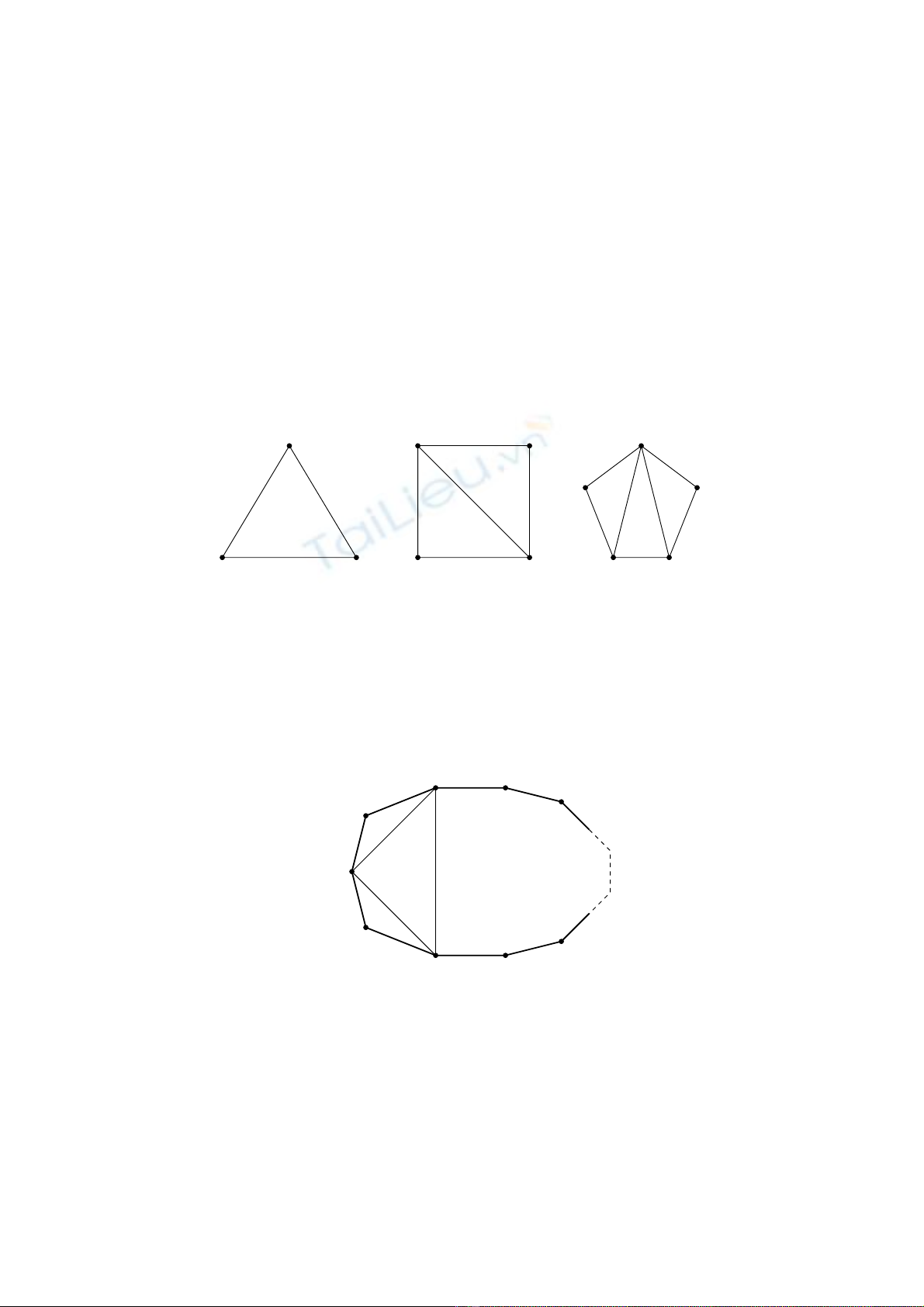
Problem 1. Let Vbe a convex polygon with nvertices.
(a) Prove that if nis divisible by 3 then Vcan be triangulated (i.e. dissected into non-overlapping
triangles whose vertices are vertices of V) so that each vertex of Vis the vertex of an odd number
of triangles.
(b) Prove that if nis not divisible by 3 then Vcan be triangulated so that there are exactly two
vertices that are the vertices of an even number of the triangles.
(20 points)
Solution. Apply induction on n. For the initial cases n= 3,4,5, chose the triangulations shown in
the Figure to prove the statement.
oddodd odd even even even
odd even odd
odd odd
odd
Now assume that the statement is true for some n=kand consider the case n=k+ 3. Denote
the vertices of Vby P1,...,Pk+3. Apply the induction hypothesis on the polygon P1P2. . . Pk; in this
triangulation each of vertices P1,...,Pkbelong to an odd number of triangles, except two vertices
if nis not divisible by 3. Now add triangles P1PkPk+2,PkPk+1Pk+2 and P1Pk+2Pk+3. This way we
introduce two new triangles at vertices P1and Pkso parity is preserved. The vertices Pk+1,Pk+2 and
Pk+3 share an odd number of triangles. Therefore, the number of vertices shared by even number of
triangles remains the same as in polygon P1P2. . . Pk.
P1P2
P3
Pkk−1
P
k−2
P
+1k
P
+2k
P
k+3
P
Problem 2. Find all functions f:R−→ Rsuch that for any real numbers a < b, the image f[a, b]
is a closed interval of length b−a.
(20 points)
1
Solution. The functions f(x) = x+cand f(x) = −x+cwith some constant cobviously satisfy
the condition of the problem. We will prove now that these are the only functions with the desired
property.
Let fbe such a function. Then fclearly satisfies |f(x)−f(y)| ≤ |x−y|for all x, y; therefore, f
is continuous. Given x, y with x < y, let a, b ∈[x, y] be such that f(a) is the maximum and f(b) is
the minimum of fon [x, y]. Then f([x, y]) = [f(b), f (a)]; hence
y−x=f(a)−f(b)≤ |a−b| ≤ y−x
This implies {a, b}={x, y}, and therefore fis a monotone function. Suppose fis increasing. Then
f(x)−f(y) = x−yimplies f(x)−x=f(y)−y, which says that f(x) = x+cfor some constant c.
Similarly, the case of a decreasing function fleads to f(x) = −x+cfor some constant c.
Problem 3. Compare tan(sin x) and sin(tan x) for all x∈(0,π
2).
(20 points)
Solution. Let f(x) = tan(sin x)−sin(tan x). Then
f0(x) = cos x
cos2(sin x)−cos(tan x)
cos2x=cos3x−cos(tan x)·cos2(sin x)
cos2x·cos2(tan x)
Let 0 < x < arctan π
2. It follows from the concavity of cosine on (0,π
2) that
3
pcos(tan x)·cos2(sin x)<1
3[cos(tan x) + 2 cos(sin x)] ≤cos tan x+ 2 sin x
3<cos x ,
the last inequality follows from tan x+2 sin x
30=1
31
cos2x+ 2 cos x≥3
q1
cos2x·cos x·cos x= 1. This
proves that cos3x−cos(tan x)·cos2(sin x)>0, so f0(x)>0, so fincreases on the interval [0,arctan π
2].
To end the proof it is enough to notice that (recall that 4 + π2<16)
tan hsin arctan π
2i= tan π/2
p1 + π2/4>tan π
4= 1 .
This implies that if x∈[arctan π
2,π
2] then tan(sin x)>1 and therefore f(x)>0.
Problem 4. Let v0be the zero vector in Rnand let v1, v2, . . . , vn+1 ∈Rnbe such that the Euclidean
norm |vi−vj|is rational for every 0 ≤i, j ≤n+ 1. Prove that v1, . . . , vn+1 are linearly dependent
over the rationals.
(20 points)
Solution. By passing to a subspace we can assume that v1, . . . , vnare linearly independent over the
reals. Then there exist λ1, . . . , λn∈Rsatisfying
vn+1 =
n
X
j=1
λjvj
We shall prove that λjis rational for all j. From
−2hvi, vji=|vi−vj|2− |vi|2− |vj|2
we get that hvi, vjiis rational for all i, j. Define Ato be the rational n×n-matrix Aij =hvi, vji,
w∈Qnto be the vector wi=hvi, vn+1i, and λ∈Rnto be the vector (λi)i. Then,
hvi, vn+1i=
n
X
j=1
λjhvi, vji
gives Aλ =w. Since v1,...,vnare linearly independent, Ais invertible. The entries of A−1are
rationals, therefore λ=A−1w∈Qn, and we are done.
2
Problem 5. Prove that there exists an infinite number of relatively prime pairs (m, n) of positive
integers such that the equation
(x+m)3=nx
has three distinct integer roots.
(20 points)
Solution. Substituting y=x+m, we can replace the equation by
y3−ny +mn = 0.
Let two roots be uand v; the third one must be w=−(u+v) since the sum is 0. The roots must
also satisfy
uv +uw +vw =−(u2+uv +v2) = −n, i.e. u2+uv +v2=n
and
uvw =−uv(u+v) = mn.
So we need some integer pairs (u, v) such that uv(u+v) is divisible by u2+uv +v2. Look for such
pairs in the form u=kp,v=kq. Then
u2+uv +v2=k2(p2+pq +q2),
and
uv(u+v) = k3pq(p+q).
Chosing p, q such that they are coprime then setting k=p2+pq +q2we have uv(u+v)
u2+uv +v2=
p2+pq +q2.
Substituting back to the original quantites, we obtain the family of cases
n= (p2+pq +q2)3, m =p2q+pq2,
and the three roots are
x1=p3, x2=q3, x3=−(p+q)3.
Problem 6. Let Ai, Bi, Si(i= 1,2,3) be invertible real 2 ×2 matrices such that
(1) not all Aihave a common real eigenvector;
(2) Ai=S−1
iBiSifor all i= 1,2,3;
(3) A1A2A3=B1B2B3=1 0
0 1.
Prove that there is an invertible real 2 ×2 matrix Ssuch that Ai=S−1BiSfor all i= 1,2,3.
(20 points)
Solution. We note that the problem is trivial if Aj=λI for some j, so suppose this is not the case.
Consider then first the situation where some Aj, say A3, has two distinct real eigenvalues. We may
assume that A3=B3=λµby conjugating both sides. Let A2= ( a b
c d ) and B2=a0b0
c0d0. Then
a+d= Tr A2= Tr B2=a0+d0
aλ +dµ = Tr(A2A3) = Tr A−1
1= Tr B−1
1= Tr(B2B3) = a0λ+d0µ.
Hence a=a0and d=d0and so also bc =b0c0. Now we cannot have c= 0 or b= 0, for then (1,0)>or
(0,1)>would be a common eigenvector of all Aj. The matrix S= ( c0
c) conjugates A2=S−1B2S,
and as Scommutes with A3=B3, it follows that Aj=S−1BjSfor all j.
3
If the distinct eigenvalues of A3=B3are not real, we know from above that Aj=S−1BjSfor
some S∈GL2Cunless all Ajhave a common eigenvector over C. Even if they do, say Ajv=λjv,
by taking the conjugate square root it follows that Aj’s can be simultaneously diagonalized. If
A2= ( ad) and B2=a0b0
c0d0, it follows as above that a=a0,d=d0and so b0c0= 0. Now B2
and B3(and hence B1too) have a common eigenvector over Cso they too can be simultaneously
diagonalized. And so SAj=BjSfor some S∈GL2Cin either case. Let S0= Re Sand S1= Im S.
By separating the real and imaginary components, we are done if either S0or S1is invertible. If not,
S0may be conjugated to some T−1S0T=x0
y0, with (x, y)>6= (0,0)>, and it follows that all Aj
have a common eigenvector T(0,1)>, a contradiction.
We are left with the case when no Ajhas distinct eigenvalues; then these eigenvalues by necessity
are real. By conjugation and division by scalars we may assume that A3= ( 1b
1) and b6= 0. By further
conjugation by upper-triangular matrices (which preserves the shape of A3up to the value of b) we can
also assume that A2= ( 0u
1v). Here v2= Tr2A2= 4 det A2=−4u. Now A1=A−1
3A−1
2=−(b+v)/u 1
1/u ,
and hence (b+v)2/u2= Tr2A1= 4 det A1=−4/u. Comparing these two it follows that b=−2v.
What we have done is simultaneously reduced all Ajto matrices whose all entries depend on uand
v(= −det A2and Tr A2, respectively) only, but these themselves are invariant under similarity. So
Bj’s can be simultaneously reduced to the very same matrices.
4