B GIÁO D C VÀ ĐÀO T OỘ Ụ Ạ Đ THI TUY N SINH Đ I H C, CAO Đ NG NĂM 2009 Ề Ể Ạ Ọ Ẳ
Đ THAM KH OỀ Ả Môn thi : TOÁN, kh i Aố
Thi th th năm hàng tu n.ử ứ ầ
I. PH N CHUNG CHO T T C CÁC THÍ SINH (Ầ Ấ Ả 7,0 đi mể)
Câu I. (2,0 đi m)ể
Cho hàm s y = ố− x3 − 3x2 + mx + 4, trong đó m là tham s th c.ố ự
1. Kh o sát s bi n thiên và v đ th c a hàm s đã cho, v i m = 0.ả ự ế ẽ ồ ị ủ ố ớ
2. Tìm t t c các giá tr c a tham s m đ hàm s đã cho ngh ch bi n trên kho ng (0 ; + ấ ả ị ủ ố ể ố ị ế ả ∞).
Câu II. (2,0 đi m)ể
1. Gi i ph ng trình: ả ươ
3
(2cos2x + cosx – 2) + (3 – 2cosx)sinx = 0
2. Gi i ph ng trình: ả ươ
2
2 4 1
2
log (x 2) log (x 5) log 8 0+ + − + =
Câu III. (1,0 đi m)ể
Tính di n tích hình ph ng gi i h n b i đ th hàm s y = ệ ẳ ớ ạ ở ồ ị ố
x
e 1+
, tr c hoành và hai đ ng th ng x = ln3, x =ụ ườ ẳ
ln8.
Câu VI. (1,0 đi m)ể
Cho hình chóp S.ABCD có đáy ABCD là hình vuông c nh a, SA = SB = a, m t ph ng (SAB) vuông góc v iạ ặ ẳ ớ
m t ph ng (ABCD). Tính bán kính m t c u ngo i ti p hình chóp S.ABCD.ặ ẳ ặ ầ ạ ế
Câu V. (1,0 đi m)ể
Xét các s th c d ng x, y, z th a mãn đi u ki n x + y + z = 1.ố ự ươ ỏ ề ệ
Tìm giá tr nh nh t c a bi u th c: ị ỏ ấ ủ ể ứ
2 2 2
x (y z) y (z x) z (x y)
Pyz zx xz
+ + +
= + +
II. PH N RIÊNG (Ầ3,0 đi mể)
Thí sinh ch đ c ch n làm m t trong hai ph n (ph n 1 ho c ph n 2)ỉ ượ ọ ộ ầ ầ ặ ầ
1. Theo ch ng trình Chu n:ươ ẩ
Câu VIa. (2,0 đi m)ể
1. Trong m t ph ng v i h t a đ Oxy, cho đ ng tròn (C) có ph ng trình: xặ ẳ ớ ệ ọ ộ ườ ươ 2 + y2 – 6x + 5 = 0. Tìm đi mể
M thu c tr c tung sao cho qua M k đ c hai ti p tuy n v i (C) mà góc gi a hai ti p tuy n đó b ng 60ộ ụ ẻ ượ ế ế ớ ữ ế ế ằ 0.
2. Trong không gian v i h t a đ Oxyz, cho đi m M(2 ; 1 ; 0) và đ ng th ng d có ph ng trình:ớ ệ ọ ộ ể ườ ẳ ươ
x 1 2t
y 1 t
z t
= +
= − +
= −
Vi t ph ng trình tham s c a đ ng th ng đi qua đi m M, c t và vuông góc v i đ ng th ng d.ế ươ ố ủ ườ ẳ ể ắ ớ ườ ẳ
Câu VIIa. (1,0 đi m)ể
Tìm h s c a xệ ố ủ 2 trong khai tri n thành đa th c c a bi u th c P = (xể ứ ủ ể ứ 2 + x – 1) 6
2. Theo ch ng trình Nâng caoươ
Câu VIb. (2,0 đi m)ể
1. Trong m t ph ng v i h t a đ Oxy, cho đ ng tròn (C) có ph ng trình: xặ ẳ ớ ệ ọ ộ ườ ươ 2 + y2 – 6x + 5 = 0. Tìm đi mể
M thu c tr c tung sao cho qua M k đ c hai ti p tuy n v i (C) mà góc gi a hai ti p tuy n đó b ng 60ộ ụ ẻ ượ ế ế ớ ữ ế ế ằ 0.
2. Trong không gian v i h t a đ Oxyz, cho đi m M(2 ; 1 ; 0) và đ ng th ng d có ph ng trình:ớ ệ ọ ộ ể ườ ẳ ươ
x 1 y 1 z
2 1 1
− +
= = −
.
Vi t ph ng trình chính t c c a đ ng th ng đi qua đi m M, c t và vuông góc v i đ ng th ng d.ế ươ ắ ủ ườ ẳ ể ắ ớ ườ ẳ
Câu VIIb. (1,0 đi m)ể
Tìm h s c a xệ ố ủ 3 trong khai tri n thành đa th c c a bi u th c P = (xể ứ ủ ể ứ 2 + x – 1)5
1
……………………H t……………………ế
Thí sinh không đ c s d ng tài li u, cán b coi thi không gi i thích gì thêm.ượ ử ụ ệ ộ ả
H và tên thí sinh: ………………………………………… S báo danh: ……………………ọ ố
2
ĐÁP ÁN – THANG ĐI MỂ
Câu Đáp án Điể
m
I
(2,0
đi m)ể
1. (1,25 đi m)ể
V i m = 0, ta có hàm s y = – xớ ố 3 – 3x2 + 4
T p xác đ nh: D = ậ ị
¡
S bi n thiên: ự ế
•Chi u bi n thiên: y’ = – 3xề ế 2 – 6x, y’ = 0 ⇔
y’ < 0 ⇔
y’ > 0 ⇔ – 2 < x < 0
Do đó: + Hàm s ngh ch bi n trên m i kho ng (ố ị ế ỗ ả − ∞ ; − 2) và (0 ; + ∞)
+ Hàm s đ ng bi n trên kho ng (ố ồ ế ả − 2 ; 0)
0,50
•C c tr : ự ị + Hàm s y đ t c c ti u t i x = – 2 và yố ạ ự ể ạ CT = y(–2) = 0;
+ Hàm s y đ t c c đ i t i x = 0 và yố ạ ự ạ ạ CĐ = y(0) = 4.
•Gi i h n: ớ ạ
x x
lim , lim
→−∞ →+∞
= +∞ = −∞
0,25
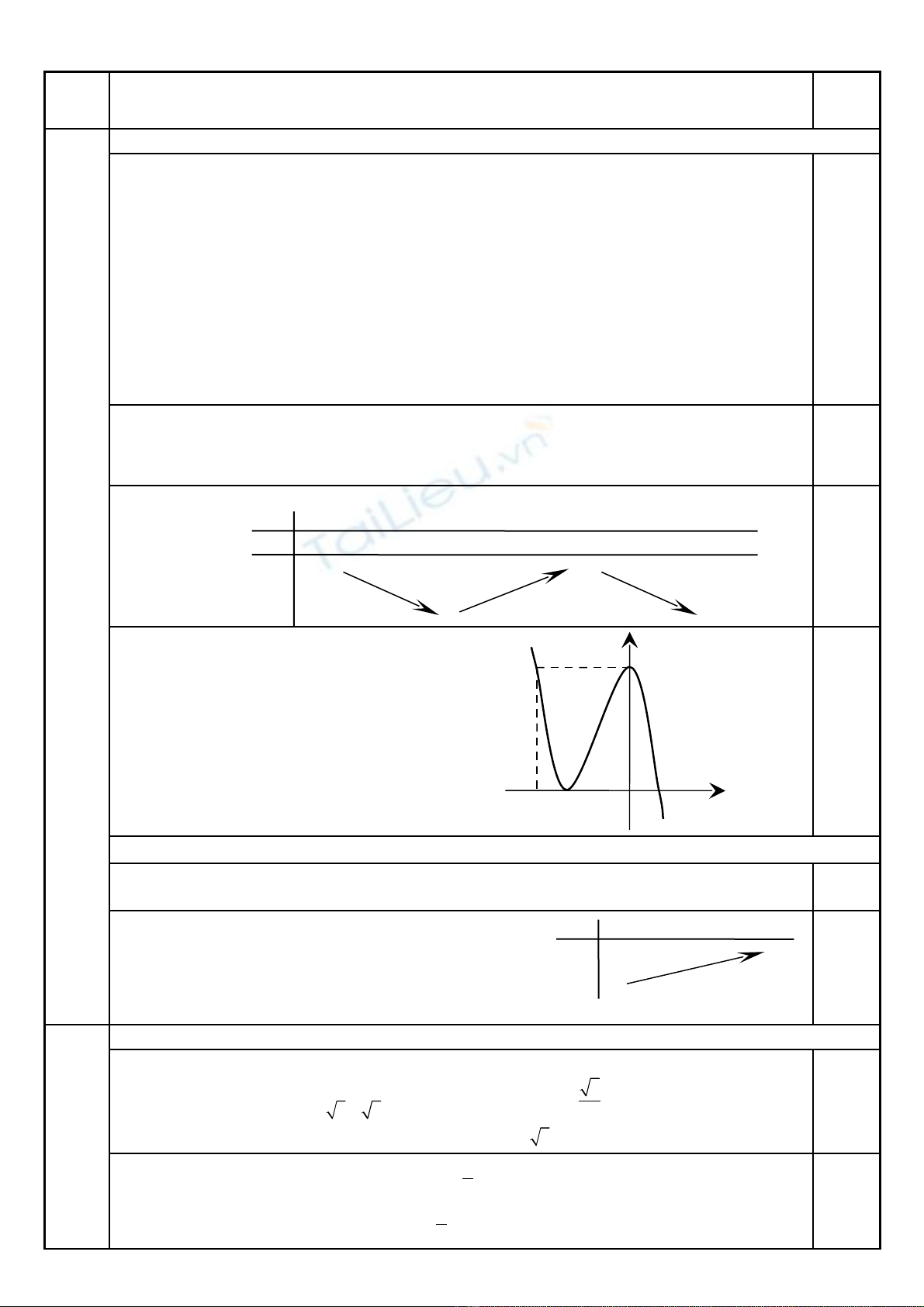
•B ng bi n thiên:ả ế
0,25
•Đ th : ồ ị
Đ th c t tr c tung t i đi m (0 ;ổ ị ắ ụ ạ ể
4), c t tr c hoành t i đi m (1 ; 0)ắ ụ ạ ể
và ti p xúc v i tr c hoành t i đi mế ớ ụ ạ ể
(− 2 ; 0) 0,25
2.(0,75 đi m)ể
Hàm s đã cho ngh ch bi n trên kho ng (0 ; + ố ị ế ả ∞)⇔ y’ = – 3x2 – 6x + m ≤ 0, ∀ x > 0
⇔ 3x2 + 6x ≥ m, ∀ x > 0 (*) 0,25
Ta có b ng bi n thiên c a hàm s y = 3xả ế ủ ố 2 + 6x trên (0 ; +
∞)
T đó ta đ c : (*) ừ ượ ⇔ m ≤ 0.
0,50
II
(2,0
đi m)ể
1. (1,0 đi m)ể
Ph ng trình đã cho t ng đ ng v i ph ng trình :ươ ươ ươ ớ ươ
( ) ( )
3
sin x
2sin x 3 3 sin x cos x 0 2
3 sin x cos x 0
=
− + = ⇔
+ =
0,50
n
x ( 1) n , n
3
x k , k
6
π
= − + π ∈
⇔π
= − + π ∈
¢
¢
0,50
3
x
y'
y
−∞
−∞
+∞
+∞
2
−
0
0
0
0
4
−
−
+
4
3
−
2
−
O
1
y
x
x
y
+∞
0
+∞
0
Câu Đáp án Điể
m
2. (1,0 đi m)ể
Đi u ki n: x > – 2 và x ề ệ ≠ 5 (*)
V i đi u ki n đó, ta có ph ng trình đã cho t ng đ ng v i ph ng trình:ớ ề ệ ươ ươ ươ ớ ươ
2 2
2 2
log (x 2) x 5 log 8 (x 2) x 5 8 (x 3x 18)(x 3x 2) 0 + − = ⇔ + − = ⇔ − − − − =
0,50
2
2
x 3x 18 0 3 17
x 3; x 6; x 2
x 3x 2 0
− − = ±
⇔ ⇔ = − = =
− − =
Đ i chi u v i đi u ki n (*), ta đ c t t c các nghi m c a ph ng trình đã cho là: ố ế ớ ề ệ ượ ấ ả ệ ủ ươ
x 6=
và
3 17
x2
±
=
0,50
III
(1,0
đi m)ể
Kí hi u S là di n tích c n tính.ệ ệ ầ
Vì
ln8
x x
ln 3
e 1 0 x [ln 3 ; ln8] nên S e 1dx+ > ∀ ∈ = +
∫
0,25
Đ t ặ
x
e 1+
= t, ta có
2
2tdt
dx t 1
=−
Khi x = ln3 thì t = 2, và khi x = ln8 thì t = 3
0,25
Vì v y: ậ
3 3 3 3 3
23 3
2 2 2 2
2 2 2 2 2
2t dt dt dt dt 3
S 2 dt 2 2 ln t 1 ln t 1 2 ln
t 1 t 1 t 1 t 1 2
= = + = + − = + − − + = +
− − − +
∫ ∫ ∫ ∫ ∫
0,50
IV
(1,0
đi m)ể
Do SA = SB = AB (= a) nên SAB là tam giác đ u.ề
G i G và I t ng ng là tâm c a tam giác đ u SAB và tâm c a hình vuông ABCD.ọ ươ ứ ủ ề ủ
G i O là tâm m t c u ngo i ti p hình chóp S.ABD.ọ ặ ầ ạ ế
Ta có OG ⊥ (SAB) và OI ⊥ (ABCD).
0,50
Suy ra: + OG = IH =
a
2
, trong đó H là trung đi m c a AB.ể ủ
+ Tam giác OGA vuông t i G.ạ
0,25
Kí hi u R là bán kính m t c u ngo i ti p hình chóp S.ABD,ệ ặ ầ ạ ế
ta có:
2 2
2 2
a 3a a 21
R OA OG GA 4 9 6
= = + = + =
0,25
V
(1,0
đi m)ể
Ta có :
2 2 2 2 2 2
x x y y z z
Py z z x x y
= + + + + +
(*)
Nh n th y : xậ ấ 2 + y2 – xy ≥ xy ∀x, y ∈
¡
Do đó : x3 + y3 ≥ xy(x + y) ∀x, y > 0 hay
2 2
x y x y
y x
+ ≥ +
∀x, y > 0
0,50
T ng t , ta có : ươ ự
2 2
y z y z
z y
+ ≥ +
∀y, z > 0
2 2
z x z x
x z
+ ≥ +
∀x, z > 0
C ng t ng v ba b t đ ng th c v a nh n đ c trên, k t h p v i (*), ta đ c:ộ ừ ế ấ ẳ ứ ừ ậ ượ ở ế ợ ớ ượ
P ≥ 2(x + y + z) = 2 ∀x, y, z > 0 và x + y + z = 1
H n n a, ta l i có P = 2 khi x = y = z = ơ ữ ạ
1
3
. Vì v y, minP = 2. ậ
0,50
VI.a
(2,0
đi m)ể
1. (1,0 đi m)ể
Vi t l i ph ng trình c a (C) d i d ng: (x – 3)ế ạ ươ ủ ướ ạ 2 + y2 = 4.
T đó, (C) có tâm I(3 ; 0) và bán kính R = 2ừ0,25
Suy ra tr c tung không có đi m chung v i đ ng tròn (C). Vì v y, qua m t đi m b t kì trên t cụ ể ớ ườ ậ ộ ể ấ ụ
tung luôn k đ c hai ti p tuy n c a (C).ẻ ượ ế ế ủ 0,25
4
A
B
C
D
H
GO
I
S
Câu Đáp án Điể
m
Xét đi m M(0 ; m) tùy ý thu c tr c tung.ể ộ ụ
Qua M, k các ti p tuy n MA và MB c a (C) (A, B là các ti p đi m). Ta có:ẻ ế ế ủ ế ể
Góc gi a 2 đ ng th ng MA và MB b ng 60ữ ườ ẳ ằ 0
·
·
0
0
AMB 60 (1)
AMB 120 (2)
=
⇔
=
0,25
Vì MI là phân giác c a ủ
·
AMB
nên :
(1)
·
0 2
0
IA
AMI 30 MI MI 2R m 9 4 m 7
sin 30
⇔ = ⇔ = ⇔ = ⇔ + = ⇔ = ±
(2)
·
0 2
0
IA 2R 3 4 3
AMI 60 MI MI m 9
sin 60 3 3
⇔ = ⇔ = ⇔ = ⇔ + =
(*)
D th y, không có m th a mãn (*)ễ ấ ỏ
V y có t t c hai đi m c n tìm là: (0 ; ậ ấ ả ể ầ −
7
) và (0 ;
7
)
0,25
2. (1,0 đi m)ể
G i H là hình chi u vuông góc c a M trên d, ta có MH là đ ng th ng đi qua M, c t và vuôngọ ế ủ ườ ẳ ắ
góc v i d.ớ0,25
Vì H ∈ d nên t a đ c a H có d ng : (1 + 2t ; ọ ộ ủ ạ − 1 + t ; − t).
Suy ra :
MH
uuuur
= (2t − 1 ; − 2 + t ; − t)
Vì MH ⊥ d và d có m t vect ch ph ng là ộ ơ ỉ ươ
u
r
= (2 ; 1 ; −1), nên :
2.(2t – 1) + 1.(− 2 + t) + (− 1).(−t) = 0 ⇔ t =
2
3
. Vì th , ế
MH
uuuur
=
1 4 2
; ;
3 3 3
− −
.
0,50
Suy ra, ph ng trình tham s c a đ ng th ng MH là: ươ ố ủ ườ ẳ
x 2 t
y 1 4t
z 2t
= +
= −
= −
0,25
VII.a
(1,0
đi m)ể
Theo công th c nh th c Niu-t n, ta có:ứ ị ứ ơ
P =
0 6 1 2 5 k 2k 6 k 5 10 6 12
6 6 6 6 6
C (x 1) C x (x 1) C x (x 1) C x (x 1) C x
−
− + − + + − + + − +K K
0,25
Suy ra, khi khai tri n P thành đa th c, xể ứ 2 ch xu t hi n khi khai tri n ỉ ấ ệ ể
0 6
6
C (x 1)−
và
1 2 5
6
C x (x 1)−
.0,25
H s c a xệ ố ủ 2 trong khai tri n ể
0 6
6
C (x 1)−
là :
0 2
6 6
C .C
H s c a xệ ố ủ 2 trong khai tri n ể
1 2 5
6
C x (x 1)−
là :
1 0
6 5
C .C−
0,25
Vì v y, h s c a xậ ệ ố ủ 2 trong khai tri n P thành đa th c là : ể ứ
0 2
6 6
C .C
1 0
6 5
C .C−
= 9. 0,25
VI.b
(2,0
đi m)ể
1. (1,0 đi m) ểXem ph n 1 Câu VI.a.ầ
2. (1,0 đi m)ể
G i H là hình chi u vuông góc c a M trên d, ta có MH là đ ng th ng đi qua M, c t và vuôngọ ế ủ ườ ẳ ắ
góc v i d.ớ0,25
d có ph ng trình tham s là: ươ ố
x 1 2t
y 1 t
z t
= +
= − +
= −
Vì H ∈ d nên t a đ c a H có d ng : (1 + 2t ; ọ ộ ủ ạ − 1 + t ; − t).
Suy ra :
MH
uuuur
= (2t − 1 ; − 2 + t ; − t)
Vì MH ⊥ d và d có m t vect ch ph ng là ộ ơ ỉ ươ
u
r
= (2 ; 1 ; −1), nên :
2.(2t – 1) + 1.(− 2 + t) + (− 1).(−t) = 0 ⇔ t =
2
3
. Vì th , ế
MH
uuuur
=
1 4 2
; ;
3 3 3
− −
.
0,50
Suy ra, ph ng trình chính t c c a đ ng th ng MH là: ươ ắ ủ ườ ẳ
x 2 y 1 z
1 4 2
− −
= =
− −
0,25
Câu Đáp án Điể
5