TRƯỜNG THPT CHUYÊN NĐC ĐỀ THI THỬ ĐẠI HỌC VÀ CAO ĐẲNG NĂM 2014
-------------------------------- Môn: TOÁN; khối D
ĐỀ THI THỬ LẦN 1 Thời gian làm bài: 180 phút, không kể phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1: (2,0 điểm) Cho hàm số
13
3
++−= xxy
(1)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2) Định tham số m để phương trình
0327
1
=+−
+
m
xx
có đúng hai nghiệm phân biệt.
Câu 2: (1,0 điểm) Giải phương trình:
0)22013cos()412sin(
2
1
2cos
2
=−−+− xxx
ππ
.
Câu 3:
(1,0 điểm)
Gi
ả
i h
ệ
ph
ươ
ng trình:
=−
=−
6).(
19
33
xyyx
yx
.
Câu 4:
(1,0 điểm)
Tìm nguyên hàm
)(xF
c
ủ
a hàm s
ố
5
2
.
6
2
1
)(
−
+
=
−xx
xf , bi
ế
t
2013)2(
=
F
.
Câu 5:
(1,0 điểm)
Trong m
ặ
t ph
ẳ
ng (P), cho hình thoi
ABCD
có
độ
dài các c
ạ
nh b
ằ
ng a; góc
0
120=
∧
ABC
.
G
ọ
i
G
là tr
ọ
ng tâm tam giác
ABD
. Trên
đườ
ng th
ẳ
ng vuông góc v
ớ
i m
ặ
t ph
ẳ
ng (P) t
ạ
i
G
l
ấ
y
đ
i
ể
m
S
sao cho
góc
0
90=
∧
ASC
. Tính th
ể
tích kh
ố
i chóp
SABCD
và kho
ả
ng cách t
ừ
đ
i
ể
m
G
đế
n m
ặ
t ph
ẳ
ng
(SBD)
theo a.
Câu 6:
(1,0 điểm)
Tìm giá tr
ị
l
ớ
n nh
ấ
t và giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a hàm s
ố
1sinsin21)( ++−= xxxf .
PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được làm một trong hai phần (Phần A hoặc B)
A. Theo chương trình chuẩn
Câu 7a: (1,0 điểm) Trong mặt phẳng Oxy, tìm các điểm M trên parabol (P):
2
xy =
sao cho khoảng cách
từ điểm M đến đường thẳng
062:)(
=
−
−
yxd
là ngắn nhất.
Câu 8a: (1,0 điểm) Giải phương trình:
xxx log1)10log()100log( 6.134.93.4
2
+
=+
.
Câu 9a: (1,0 điểm) Tìm hệ số của số hạng chứa
7
x
trong khai triển
n
x
x
−2
3
2
, biết hệ số của số hạng thứ
ba bằng
1080
.
B. Theo chương trình nâng cao
Câu 7b: (1,0 điểm) Trong mặt phẳng Oxy, lấy hai điểm
)1;1(
−
A
và
)9;3(B
nằm trên parabol
2
:)(
xyP
=
.
Điểm M thuộc cung AB. Tìm toạ độ điểm M sao cho diện tích tam giác ABM đạt lớn nhất.
Câu 8b: (1,0 điểm) Giải bất phương trình:
0
2
3
2
)1(log)1(log
2
4
3
2
2
>
−
+
−−−
x
x
xx
.
Câu 9b: (1,0 điểm) Từ khai triển của biểu thức
10099
2
98
99
1
100
0
100
...)1( axaxaxaxax +++++=− .
Tính tổng 12.12.2...2.992.100
1
99
2
98
99
1
100
0
+++++= aaaaS .
----------------- Hết -----------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………………; Số báo danh:……………………………
www.MATHVN.com
www.DeThiThuDaiHoc.com
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC LẦN 1 KHỐI D NĂM HỌC 2013 – 2014
Câu Nội dung Điểm
1) Khảo sát
13
3
++−=
xxy
1,00
+ TXĐ:
R
D
=
+ Giới hạn:
+∞
=
−∞→
y
x
lim
;
−∞
=
+∞→
y
x
lim
+ Sự biến thiên:
33'
2
+−= xy
;
=
−=
⇔=+−⇔= 1
1
0330' 2
x
x
xy
0,25
Hàm số nghịch biến trên khoảng
(
)
(
)
+
−
−
;1;1;
Hàm số đồng biến trên khoảng
(
)
1;1
−
Hàm số đạt cực đại tại x = 1, y
CĐ
= 3; đạt cực tiểu tại x =
−
1, y
CT
=
−
1
0,25
+ Bảng biến thiên
x
−∞
−
1 1
+∞
y
′
−
0 + 0
−
y
+∞
3
−
1
−∞
0,25
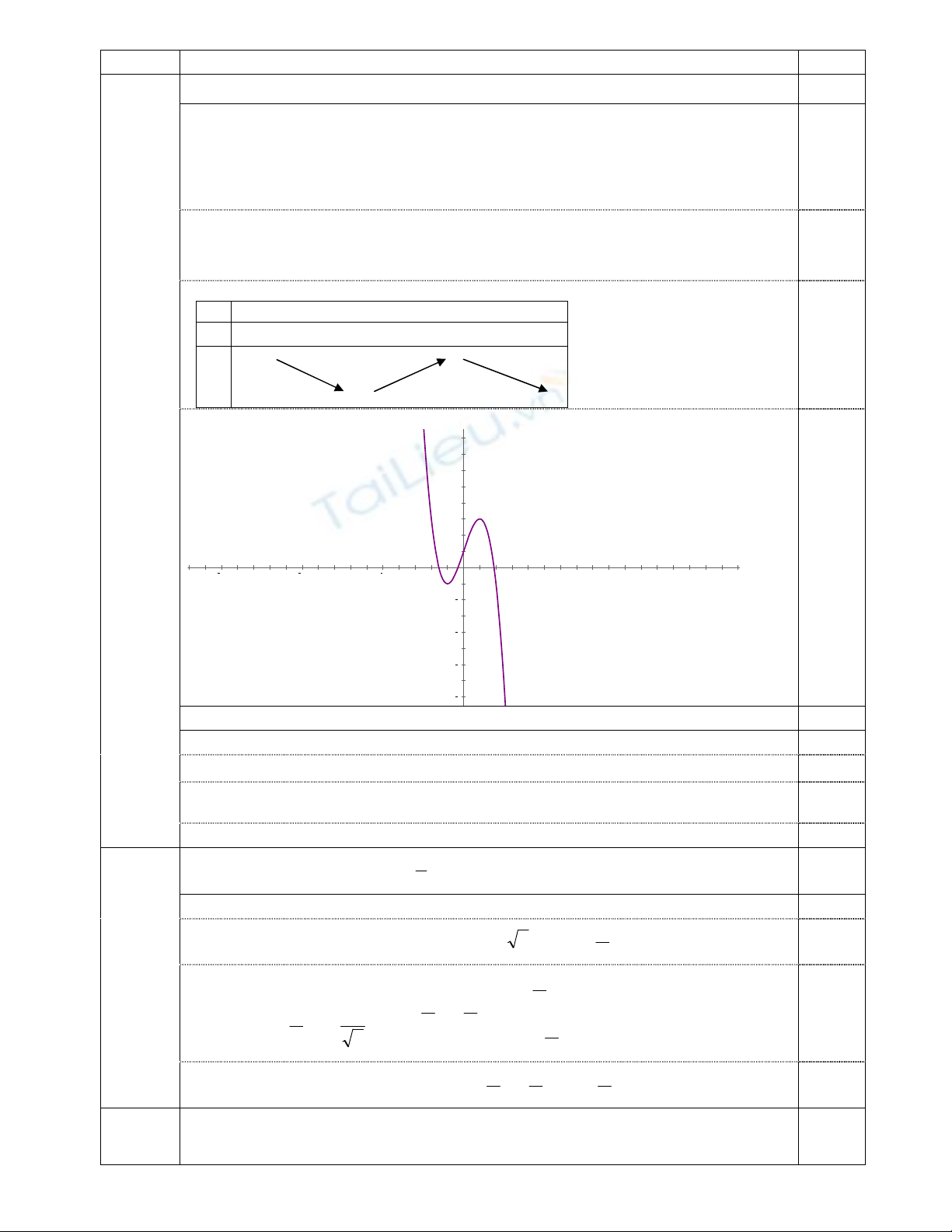
+ Đồ thị: đồ thị hàm số cắt trục tung tại điểm (0; 1).
8
6
4
2
2
4
6
8
15 10 5 5 10 15
0,25
2) Định m để pt
0327
1
=+−
+
m
xx
có đúng hai nghiệm phân biệt. 1,00
+ Đặt:
x
X3=
, điều kiện
0
>
X
0,25
+ Ta có pt
0,113
3>∀+=++−⇒XmXX
0,25
+ Số nghiệm của pt là số giao điểm của (C) và đường thẳng y = m+1 trên miền
0
>
X
. 0,25
Câu 1
+ Dựa vào đồ thị ta có
311
<
+
<
m
⇔
20
<
<
m
. 0,25
Giải phương trình:
0)22013cos()412sin(
2
1
2cos
2
=−−+− xxx
ππ
1,00
+ pt t
ươ
ng
đươ
ng 02cos2cos.2sin2cos
2
=+− xxxx 0,25
0)12sin2(cos2cos
=
+
−
⇔
xxx
0]1)
4
2cos(2.[2cos =++⇔
π
xx 0,25
−=+
=
⇔
2
1
)
4
2cos(
02cos
π
x
x
∨+=⇔
2
4
π
π
kx
Zk
kx
kx
∈
+−=
+=
,
2
4
π
π
π
π
0,25
Câu 2
+ KL: ph
ươ
ng trình có hai h
ọ
nghi
ệ
m Zkkxkx ∈+−=+= ,
2
,
2
4
π
π
π
π
0,25
Câu 3
Giải hệ phương trình:
=−
=−
6).(
19
33
xyyx
yx
1,00
www.MATHVN.com
www.DeThiThuDaiHoc.com
+ Hpt t
ươ
ng
đươ
ng v
ớ
i
=−
=+−−
6).(
19]3))[((
2
xyyx
xyyxyx
0,25
+
Đặ
t
xyPyxH
=
−
=
;
⇒
=
=+
6.
19)3(
2
PH
PHH 0,25
=
=
⇒6
1
P
H
. 0,25
+ KL: hpt có 2 cặp nghiệm
)2;3(
=
=
yx
và
)3;2(
−
=
−
=
yx
0,25
Tìm nguyên hàm F(x) của hàm số
5
2
.
6
2
1
)(
−
+
=
−xx
xf , biết F(2) = 2013.
1,00
∫
dxxf )(
=
∫
+
−
dx
xx
x
6
2
.
5
2
2
2
, đặt
dxdtt
xx
2.2ln2
=→=
=
∫
+
−
6
5
2
ln
1
t
t
dt
x
=
∫
−
−
−dt
tt 2
1
3
1
2ln
1
0,25
= C
x
x
+
−
−
22
32
ln.
2ln
1= C
x
x
+
−
−
22
32
log
2
= F(x). 0,25
+ 2013)
2
1
(log)2(
2
=+= CF
2014
=
⇒
C
. 0,25
Câu 4
+ 2014
22
32
log)(
2
+
−
−
=
x
x
xF . 0,25
Cho hình thoi ABCD có độ dài các cạnh bằng a, góc
0
120=
∧
B
. Gọi G là trọng
tâm tam giác ABD. Trên đường thẳng vuông góc với mặt phẳng đáy tại G lấy
điểm S sao cho góc
0
90=
∧
ASC
. Tính thể tích khối chóp SABCD và khoảng cách
từ điểm G đến mặt phẳng (SBD.
1,00
O
G
B
C
A
D
S
H
+
0
120=
∧
B
0
60=⇒
∧
A
⇒
ABD
∆
đều cạnh a
⇒
2
3
2
2
a
SS
ABDABCD
==
.
+ Gọi O giao điểm AC và BD
2
3.a
AO =⇒
;
3
3.
3
2a
AOAG ==
;
3aAC =
3
6.
.a
GCGASG ==⇒
(
SAC
∆
vuông tại S, đường cao SG)
0,25
+
6
2
.
3
1
3
a
SGSV
ABCDSABCD
==
. 0,25
+ Kẻ GH
⊥
SO
⇒
GH
⊥
(SBD) vì BD
⊥
GH
(SAO)
⇒
GHSBDGd
=
))(,(
0,25
Câu 5
+
SGO
∆
vuông tại G, đường cao GH
⇒
2222
2
27111
a
GO
GS
GH
=+=
0,25
www.MATHVN.com
www.DeThiThuDaiHoc.com
⇒
9
6
)),(
a
GHSBDGd ==
.
Tìm GTLN và GTNN của hàm số 1sinsin21)(
++−= xxxf
. 1,00
+ Đặt
xt sin
=
2
1
1,121)(
≤≤−++−=
⇒
ttttf
0,25
+
)
2
1
;1(,
12
1
212
2
)(' −≠
+
+
−
−
=t
tt
tf
+
2
1
21120)('
−=⇔−=+⇔= ttttf
.
0,25
+
2
6
)
2
1
(;
2
23
)
2
1
(;3)1( ==−=− fff
. 0,25
Câu 6
+ KL:
2
23
max =f
khi
2
1
sin
−=x
và
2
6
min =f
khi
2
1
sin
=x
. 0,25
Tìm M trên parabol (P):
2
xy =
sao cho khoảng cách từ điểm M đến đường
thẳng (d): 2x – y – 6 = 0 ngắn nhất.
1,00
+
);()(
2
mmMPM
⇒
∈
. 0,25
+
5
62
))(;(
2
−−
=mm
dMd = 5
5
5)1(
2
≥
+−m 0,25
+ D
ấ
u “=” x
ả
y ra khi m = 1.
0,25
Câu 7a
+
KL: M(1; 1) 0,25
Giải phương trình:
xxx
log1)10log()100log(
6.134.93.4
2
+
=+
. 1,00
+ Pt t
ươ
ng
đươ
ng v
ớ
i
09
2
3
13
4
9
.4
)10log()10log(
=+
−
xx
,
0
>
x
0,25
+ Đặt 0,
2
3
)10log(
>
=tt
x
0913.4
2
=+−
⇒
tt
=
=
⇒
1
4
9
t
t 0,25
=
=
⇒
0)10log(
2)10log(
x
x
=
=
⇒
10
1
10
x
x
. 0,25
Câu 8a
+ KL: pt có hai nghiệm
10
1
;10 == xx . 0,25
Tìm hệ số của số hạng chứa
7
x
trong khai triển
n
x
x
−2
3
2
, biết hệ số của số
hạng thứ ba bằng
1080
.
1,00
+ Số hạng tổng quát
knkknk
nk
xCT
32
1
.)2.(3.
−−
+
−= 0,25
+ Số hạng thứ ba: k = 2 10804.3.
22
=
⇒
−
n
n
C
⇒
5
3.5.43.)1( =−
n
nn
5
=
⇒
n
. 0,25
+
1
3107
=
⇒
=
−
kxx
k
0,25
Câu 9a
+ Hệ số 810)2.(3.
41
5
−=−C 0,25
Hai điểm
)1;1(
−
A
và
)9;3(B
nằm trên parabol
2
:)( xyP =
. Điểm M thuộc cung
AB. Tìm M sao cho diện tích tam giác ABM đạt lớn nhất.
1,00
+
31,);()(
2
≤≤−
⇒
∈mmmMPM
0,25
+
ABM
S
∆
lớn nhất
),( ABMd
⇔
lớn nhất 0,25
Câu 7b
+ AB:
032
=
+
−
yx
.
+ 5
4
5
)1(4
),(
2
≤
−−
=m
ABMd . Dấu “=” xảy ra khi m = 1.
0,25
www.MATHVN.com
www.DeThiThuDaiHoc.com
+ KL :
)1;1(
M
. 0,25
Giải bất phương trình:
0
2
3
2
)1(log)1(log
2
4
3
2
2
>
−
+
−−−
x
x
xx
.
1,00
+ Bpt tương đương với
0
2
3
2
1log).2log21(2
2
23
>
−
+
−−
x
x
x
,
1
≠
x
02log21,0
2
3
2
1log
3
2
2
<−<
−
+
−
⇔vì
x
x
x
0,25
+ TH
1
:
>−+
<−
0232
01log
2
2
xx
x
<∨−<
<−≠
⇔
xx
x
2
1
2
110
211
2
1<<∨<<⇔ xx . 0,25
+ TH
2
:
<−+
>−
0232
01log
2
2
xx
x
<<−
>−
⇔
2
1
2
11
x
x
02
<
<
−
⇔
x
. 0,25
Câu 8b
+ KL: Tập nghiệm )2;1()1;
2
1
()0;2( ∪∪−=S. 0,25
Từ khai triển biểu thức
10099
2
98
99
1
100
0
100
...)1( axaxaxaxax +++++=−
(1)
Tính tổng 12.2.2...2.992.100
99
2
98
99
1
100
0
+++++= aaaaS .
1,00
+ Lấy đạo hàm hai vế của (1):
9998
98
1
99
0
99
2...99100)1(100 axaxaxax ++++=− 0,25
+ Nhân hai vế cho x: xaxaxaxaxx
99
2
98
99
1
100
0
99
2...99100)1(100 ++++=− 0,25
+ Cộng hai vế cho 1, thay x = 2:
Saaaa =+++++=+− 1222...29921001)12(200
99
2
98
99
1
100
0
99
0,25
Câu 9b
+ KL:
201
=
S
. 0,25
www.MATHVN.com
www.DeThiThuDaiHoc.com