


              !" # $% &'
 ()*(
+
),'-.)/(
0
1

234 567%,'-891 :;,'-
 <
.<
=
.)/(
0
1)&>%.()*(
(
?@
A(BC)0
?(*)(:
?(/):(0
<<&
D
+
B(
B00
B
B −
−
−
≈=−=
B EFG,=HI;7J=3K$L)
$",'-=)/(
0
1)&M6N-O$#)/P(
BP
&

 5-891 899J=3K)O@

B
B
B
B
B
Q
DR
&<
D−=−=
?L:(B*)
?(/P):(/P)/
?(/):(0
Q
&<
D
D
C/
BBP
B00
B
B
B
≈==
−−
−
C <>LS& OT$%&'T&M6N6NU
LHN3HS-"=V;2&W
%<>LX,'<
(
.Y(
P
1)FOHN3$
Z$#/(
(
'&M6N-%<>L"&>%[\"
<>L$#.B(


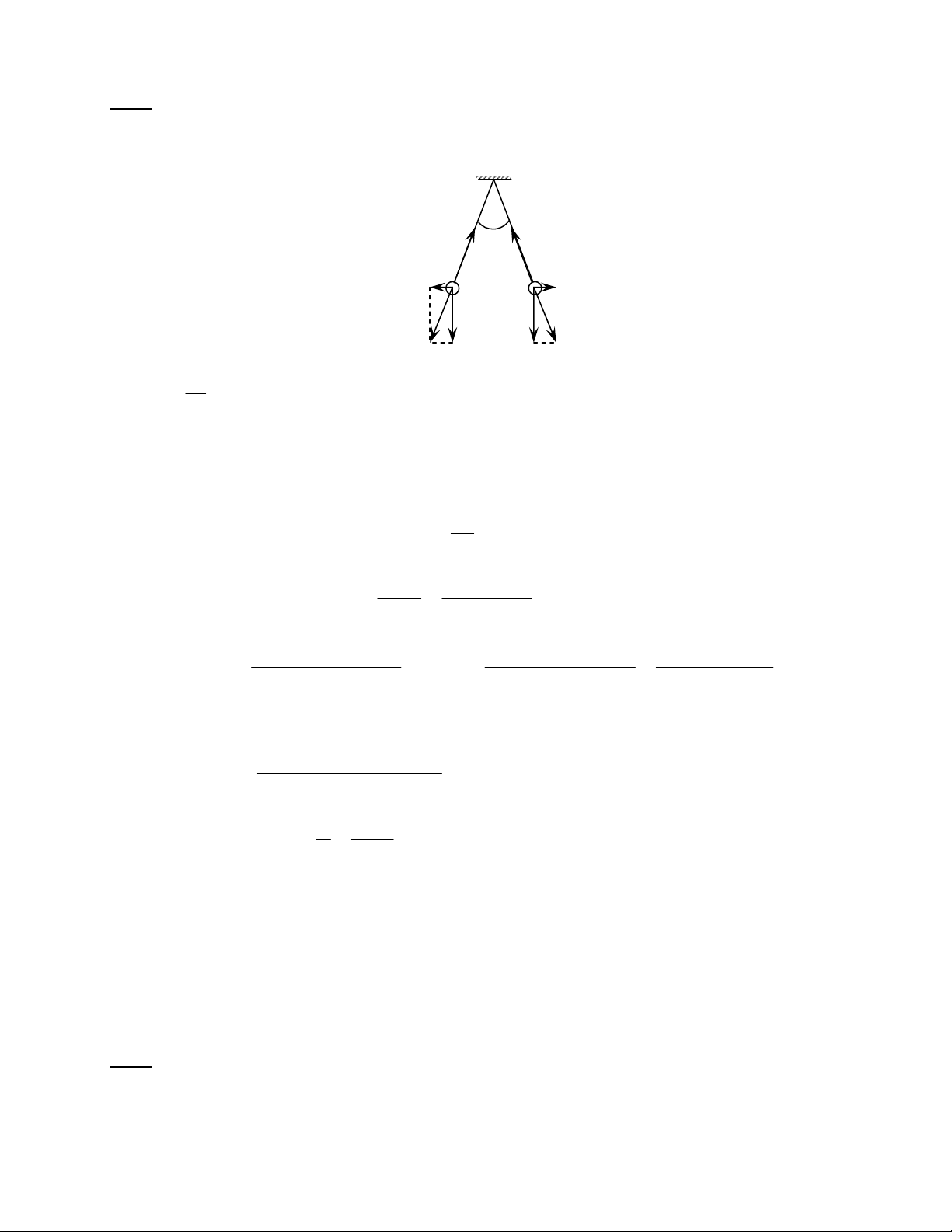
]%<>LM,'^<>L96N@
1(B
B
<
<<
P
(
B
−
===
<>L$#&@
(D_
3
=++
`O)3a39J@
P
F
tg
d
=
α
; _. 
( )
2
2
0
2
21
sin.24
α
l
kq
r
qkq
F
d
==
ααααπεεαπεε
α
tgl
kq
tgl
q
P
Pl
q
tg .sin.16.sin64.sin16.4
22
2
0
22
0
2
0
22
0
2
0
==
=
HM@
(
)
( ) ( )
)(157,0
30.30sin.2,0.16
10.4.10.9.1
0022
2
79
N
tg
P==
−
)(16)(016,0
81,9
157,0 gkg
g
P
m
====
Y '&M6N-J<>L$C!"#&%<>
L3Lb)OHN3$Zc$#*Y
(
:ε.BM;3L
b?

D

_
B
α

[&"<>$C)dOM;<>LS& &'@
11
22
01
2
0
.sin64
ααεπε
tgl
q
P
= :?
`  % <> L  3L >) ^ <> L HI 8  % 34 -  F
eHf_
6;6NW;g]O)$#'%67$)
6N@
22
22
02
2
0
1
.sin64
ααεπε
tgl
q
PP
=− :B?
hS&%@
VgPVgmgP
01
;
ρρ
=== :C?
[:?):B?:C?)O@
ρ
ρρ
ααε
ααε
0
22
2
2
11
2
11
.sin
.sin
−
==
−
tg
tg
P
PP
)(tg.sin.tg.sin
022
2
211
2
1
ρρααερααε
−=
11
2
122
2
2
22
2
2
0
tg.sin.tg.sin.
tg.sin.
.
ααεααε
ααε
ρρ
−
=
HM;@
)/(800;27;30;2;1
3
0
0
2
0
121
mkg=====
ρααεε
)/(2550800.
30.30sin27.27sin
27.27sin
3
002002
002
mkg
tgtg
tg =
−2.
2.
=
ρ
* <>L,O$%&'&M6N$#6NULHN
3OW3$#A6ZXJ, :3L?O
&M6Nρ
#HM, εb&M6N-<>L:ρ?=>
$#$ \O %HN 3  &  &',    6



234%'%dU$Y)
1,,
1210
===
εεερρ
)O@
22
2
1
2
1
11
2
22
2
22
2
1
.sin
.sin.sin.sin.
.sin.
.
αα
αα
ε
ε
ρ
ααααε
ααε
ρρ
tg
tgtgtg
tg
−
=
−
=
i;W&,O,%HN3& &'J, 6@
22
2
11
2
21
.sin.sin
αααααα
tgtg =
=
$\5U@

1
1
ρ
ε
ε
ρ
−
=
/ hX,')&M6N\XWX<jk$%
&'< l%89M\X-
<j1.)/(
0
1).0)(
B+
&)&>%$[
" . (
+


m \XV<<jk36;%34-6;
'1 

Coulombht
FF =
2
0
22
r4
e
r
v
m
πεε
=
mr4
e
r4.m
e.r
v
0
2
2
0
2
2
πεε
πεε
==
mr2
e
mr4
e
v
0
0
2
πεε
πεε
==
HM)O@
)/(10.6,1
10.10.1,9.10.86,8.1.2
10.6,1
6
103112
19
smv ==
−−−
−
π

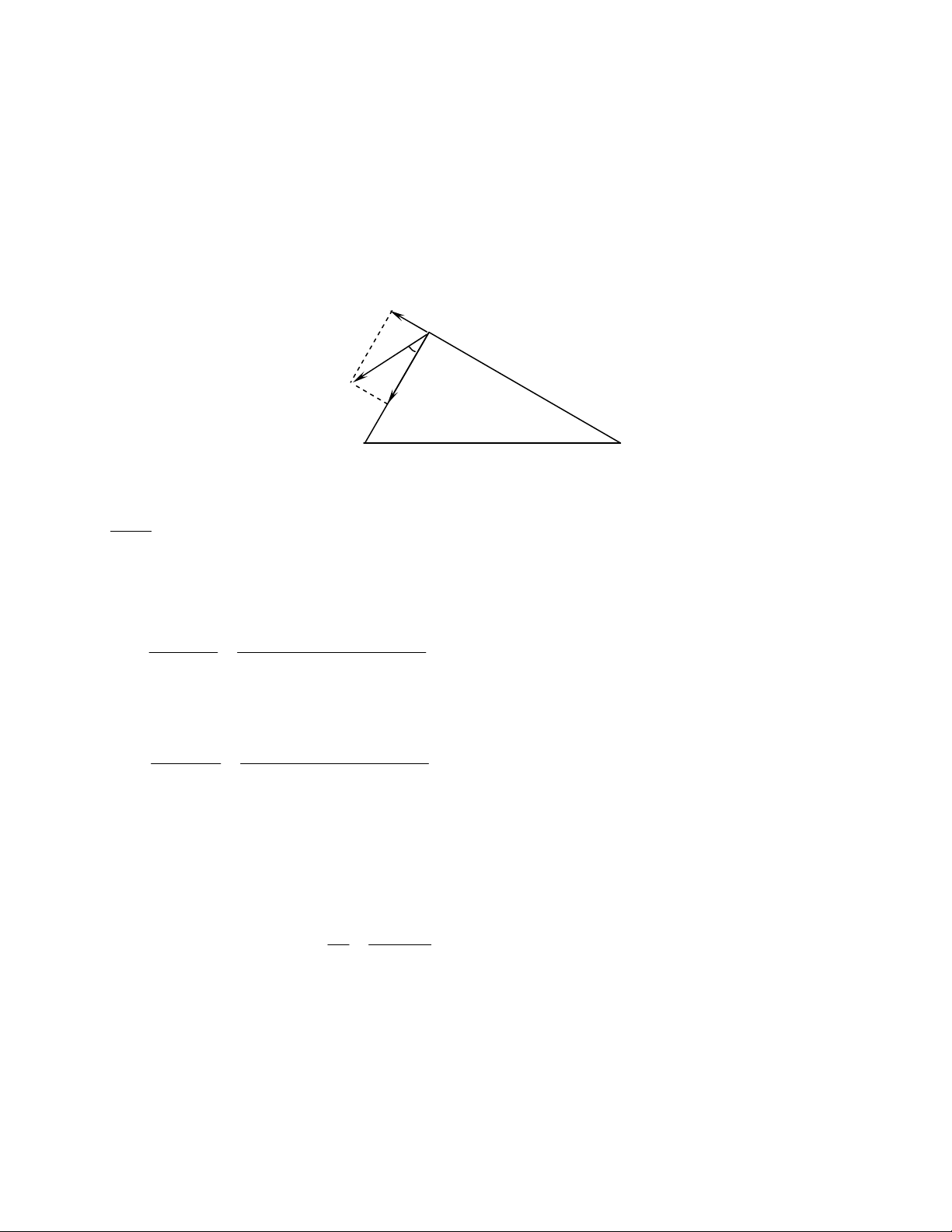
P %ce)!)1-X%6ZL6NS%,'\@<
.C(
+
1R<
B
.*(
+
1R<
C
.((
+
1l%8%34nN=,'
Se 1 $" e1. C) e!.Y) !1 .*1%, 'WS 
& &'

O@
oE
1
F
-<
B
%34<
@
)(10.4,8
)10.4.(10.86,8.1.4
10.5.10.3
4
3
2212
88
2
0
21
1
N
r
qq
F
AB
−
−−
−−
===
ππεε
oE
2
F
-<
C
%34<
@
)(10.30
)10.3.(10.86,8.1.4
10.10.10.3
4
3
2212
88
2
0
31
2
N
r
qq
F
AC
−
−−
−−
===
ππεε
o]a39J@
222
ACABBC +=
i9)%e!1 e`O@
E
F
O=67N=;e1XOV%8$U@

'421528,0
10.30
10.4,8
0
3
3
2
1
=
≈==
−
−
αα
F
F
tg
1W-
F
6I
pX;-6N'$#@
e
!
1
F
2
F
1
F