http://www.ebook.edu.vn
CHƯƠNG V: TÍNH TOÁN CÁC HẰNG SỐ CỦA THUỐC
THỬ VÀ PHỨC
V.1. NGHIÊN CỨU CƠ CHẾ TẠO PHỨC ĐƠN PHỐI TỬ
Nghiên cứu để đưa ra một phức vào ứng dụng trong thực hành phân tích thì việc nghiên
cứu cơ chế tạo phức là một bước quan trọng.
Chỉ trên cơ sở nghiên cứu cơ chế tạo phức ta mới có thể xác định dạng tồn tại cuối cùng
của ion trung tâm và phối tử cũng như viết được phản ứng tạo phức thực xảy ra trong hệ
nghiên cứu. Từ cơ chế tạo phức ta tính được hằng số cân bằng của phản ứng tạo phức thực
và hằng số bền điều kiện của phức .
Ngoài ra, khi nghiên cứu cơ chế tạo phức còn cho ta một số dữ kiện cần thiết để có thể
hiểu sâu hơn về cấu trúc của phức, dạng tồn tại của ion trung tâm và phối tử, số proton tách
ra khi tạo phức, ...
V.1.1. Nguyên tắc
Nguyên tắc chung là tìm phương trình thể hiện mối liên hệ các dạng tồn tại của ion trung
tâm, của phối tử, số phối trí, số proton, pH. Trên cơ sở đó thiết lập các thí nghiệm để tính ra
được số proton bị thay thế. Kết quả chúng ta biết được dạng ion tham gia và hằng số không
bền.
V.1.2. Các bước chính để xây dựng nghiên cứu
⎯ Đặt tên và gọi nồng độ của kim loại, thuốc thử, phức:
Để đơn giản chúng ta không ghi điện tích của các phối tử trong hệ. Gọi M là ion kim
loại và nồng độ ion kim loại là CM
Hm+1R là thuốc thử và CR là nồng độ thuốc thử
[M(OH)i(Hm-n)q] là phức và CK là nồng độ của phức
⎯ Các cân bằng của ion trung tâm trong dung dịch:
M + H2O ⇔ MOH + H K1
M(OH) + H2O ⇔ M(OH)2 + H K2
M(OH)2 + H2O ⇔ M(OH)3 + H K3
M(OH)i-1 + H2O ⇔ M(OH)i + H Ki
……………………………………..
Hằng số cân bằng của các phản ứng được biểu diễn như sau:
1
[M(OH)].[H]
K= [M]
Ta suy ra: -1
11
K.[M]
[M(OH)]= =K .[M].h
[H]
Tương tự 2
2
[M(OH) ][H]
K= [M(OH)]
http://www.ebook.edu.vn
Và -2
2
212
K[M(OH)]
[M(OH) ]= =K .K .[M]h
[H]
……………………………………………
Một cách tổng quát:
[
]
[
]
[]
i
i
i
M(OH . H
K= M(OH)
Và
[
]
[
]
-i
i12i
M(OH) =K .K ...K . M .h
Theo định luật bảo toàn nồng độ ban đầu:
[
]
(
)
(
)
(
)
⎡
⎤
⎡⎤⎡ ⎤
⎣⎦⎣ ⎦
⎣
⎦
M2
i
C = M + M OH + M OH +...+ M OH (5.1)
Thay các giá trị nồng độ của ion kim loại [M(OH), [M(OH)2]…, [M(OH)i] vào phương
trình (5.1) ta có:
[
]
[
]
[
]
[
]
-1 -2 -i
M1 12 12i K
C = M +K M h +K K M h +...K K ...K M h +C
[
]
(
)
-1 -2 -i
MK 1 12 12 i
C -C = M 1+K h +K K h +...+K K ...K h
Ta có thể tổng quát như sau:
[]
MK
-1 -2 -i
112 12i
(C C )
M=
1+K .h +K .K .h +....+K .K ...K .h
−
(5.2)
[]
MK 12i
i-1 -2 -i i
112 12i
(C C ) K .K ...K
M(OH) = .
1+K .h +K .K .h +....+K .K ...K .h h
− (5.3)
⎯ Cân bằng của thuốc thử trong dung dịch:
m+1 m
HR HR+H
฀฀฀
฀฀฀ K0'
mm-1
HR H R+H
฀฀฀
฀฀฀ K1'
m-1 m-2
HR HR+H
฀฀฀
฀฀฀ K2'
…………………………..
()
m-n
m- n-1
HR HR+H
฀฀฀
฀฀฀ Kn'
Hằng số phân ly của thuốc thử trong dung dịch là:
[
]
[
]
[]
m
'0
m+1
HR.H
K= HR
Từ đó có thể rút ra được nồng độ của thuốc thử theo biểu thức:
[]
[
]
m
m+1 '0
HRh
HR=K
Tương tự
[
]
[
]
[]
m-1
'
1
m
HR.H
K= HR
http://www.ebook.edu.vn
Và có thể rút ra:
[
]
[
]
'-1
m-1 1 m
HR=KHRh
Tổng quát:
[
]
[
]
()
m-n
'n
m- n-1
HR.H
K= HR
⎤
⎦
Và:
[
]
[
]
'' ' -n
m-n 1 2 n m
H =K .K ...K . H R h
Theo định luật bảo toàn nồng độ ban đầu đối với thuốc thử, ta có:
[
]
[
]
[
]
[
]
[
]
R m+1 m m-1 m-2 m-n K
C = H R + H R + H R + H R +...+ H R +qC (5.4)
Thay các giá trị [Hm+1R] , [HmR] , [Hm-1R] , ... , [Hm-nR] vào phương trình (5.4)
''' '''
m1m12m12nm
Rm K
'2n
0
[H R].h K .[H R] K .K .[H R] K .K ...K .[H R]
C = +[H R]+ + +...+ +qC
Khh h
(5.4)
Chuyển qCK qua vế trái ta có phương trình:
''' ''
112 12m
RKm '2 n
0
KK.K K.K.[HR]
h
C qC =[H R] +1+ + +...+
Khh h
⎛⎞
−⎜⎟
⎝⎠
(5.5)
Từ đây ta tính được nồng độ cân bằng của thuốc thử ở trạng thái cân bằng:
Dạng tổng quát của thuốc thử lúc ban đầu là:
[]
'' '
RK 12n
m-n ''' ''' n
112 12n
'2 n
0
C qC K .K ...K
HR= .
K K .K K .K ...K h
h
1+ + + +...+
Kh h h
− (5.6)
⎯ Cân bằng tạo phức:
Phản ứng tạo phức xảy ra như sau:
()
(
)
(
)
mm-n
iiq
M OH +qH R M OH H R +qnH
฀฀฀
฀฀฀ K
p (5.7)
Áp dụng định luật tác dụng khối lượng ta có phương trình (5.8)
[]
[][]
[]
[][]
qn qn
imnq K
Pqq
im im
M(OH) (H R) . H C.H
KM(OH) . H R M(OH) . H R
−
⎡⎤
⎣⎦
==
(5.8)
Hằng số bền điều kiện của phức (β) tương ứng với cân bằng tạo phức:
()
(
)
(
)
mn mn
iiq
MOH qH R MOH H R
−−
+฀฀฀
฀฀฀ β (5.9)
[][][][]
imnq K
qq
imn imn
M(OH) (H R) C
M(OH) . H R M(OH) . H R
−
−−
⎡⎤
⎣⎦
β= = (5.10)
Từ đó tính được hằng số không bền theo (5.11)
[
]
[
]
q
imn
Kb
K
M(OH) . H R 1
KC
−
=
=
β
(5.11)
http://www.ebook.edu.vn
Thay phương trình (5.6) vào (5.11) ta có (5.12)
[
]
q'' 'q
iR K 12 n
Kb ''' ''' qn
q
112 12n
K'2 n
0
M(OH) .(C qC ) (K .K ...K )
K.
K K .K K .K ...K h
h
C (1 ... )
Kh h h
−
=
+++ ++
(5.12)
Đặt:
q
iR K
''' '''
q
112 123
K'2 n
0
'' 'q
12 n
[M(OH) ].(C qC )
BKK.K K.K.K
h
C (1 ... )
Kh h h
Q (K .K ...K )
−
=
+++ ++
=
(5.13)
Ta có : cb q.n
B.Q
Kh
=
Lấy logarit 2 vế, ta được
Kb
K
lgB lg qnlgH
Q
=+
Kb
K
lgB qn.pH lg Q
−= − (5.14)
(
)
lgB f pH−=
Phương trình biểu diễn sự phụ thuộc –lgB vào pH là tuyến tính khi hệ số góc tgα=qn là
một số nguyên dương. Vì q.n là số nguyên dương (q là hệ số tỉ lượng trong phức, n là
proton tách ra từ một phân tử thuốc thử do tạo phức)
Để vẽ đường biểu diễn Kb
K
lgB qn.pH lg Q
−= − , ta cần tính B theo công thức:
[
]
q
iR K
''' '''
q
112 12n
K'2 n
0
M(OH) .(C qC )
BK K .K K .K ...K
h
C (1 ... )
Kh h h
−
=
+++ ++
Muốn tính B ta cần xác định CK
i
KM
gh
A
CC
A
=
Trong đó: CM là nồng độ ban đầu của ion trung tâm
Agh là giá trị cực đại của mật độ quang
–Agh xác định như sau:
http://www.ebook.edu.vn
Cần lưu ý rằng ta chỉ lấy giá trị pHi và Ai trên đoạn phụ thuộc tuyến tính MN (Cách
điểm uốn 0 về 2 phía khoảng 0,5 đơn vị pH)
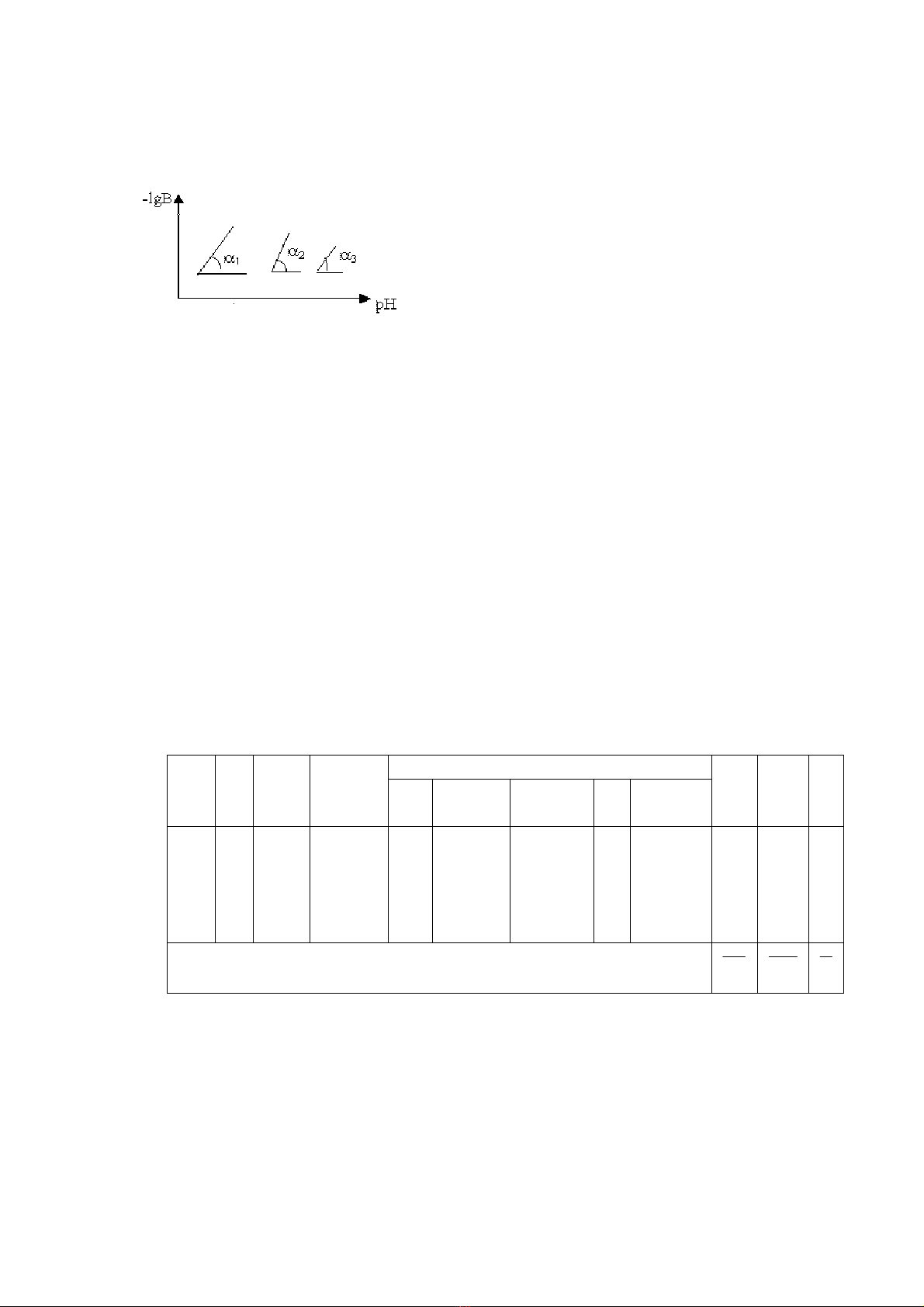
Đường biểu diễn –lgB=f(pH) có dạng như sau:
Giá trị tgα có thể có giá trị tgα<0, tgα>0 nhưng vì tgα=q.n (q.n: số nguyên dương) nên
chỉ nhận đường thẳng nào có giá trị tgα là số nguyên dương
⎯ Nếu có các đường thẳng –lgB=f(pH) cùng thỏa mãn điều kiện nguyên và dương thì có
thể có khả năng đồng thời tồn tại trong hệ hai hay nhiều phức
⎯ Nếu trong hệ chỉ tạo một phức đơn nhân thì ta chỉ lấy giá trị i nào nhỏ hơn trong các giá
trị i có tgα nguyên và dương
V.1.3. Xây dựng kế hoạch thực nghiệm
⎯ Pha dung dịch ion kim loại và thuốc thử có nồng độ phù hợp với thực nghiệm (CM, CR)
⎯ Xác định thành phần phức (q)
⎯ Cho pH của phức thay đổi tại một nồng độ nhất định từ đó tính nồng độ CK để suy ra B
⎯ Chọn i các giá trị (i từ 0 đến i)
Lập bảng 5.1:
Bảng 5.1
–lgB
pHi A
i C
K(i) CR-qCK M
i=0
M(OH)
i=1
M(OH)2
i=2 …M(OH)i
i=i
Kp K
Kb β
pH1
pH2
pH3
-
-
A1
A2
A3
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
…
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
P
K Kb
K
β
Vẽ đồ thị và chọn đường có hệ số góc tg α nguyên dương (xác định được i)
⎯ Biện luận để tìm nq và KKb
Từ giá trị tgα=nq. Nếu biết được tgα (tgα là hệ số góc của đường: –lgB=f(pH) và q là
hệ số tỉ lượng trong phức, ta suy ra n và từ đó tính được KKb, Kp
Xác định được giá trị i và n thì ta biết được dạng tồn tại cuối cùng của ion trung tâm và
anion thuốc thử Hm-nR và viết được cơ chế phản ứng tạo phức.
Nếu trong hệ tạo một phức không tan, có tích số tan Tt