Gv: Lê Minh Gi yấ THPT Th Khoa Nghĩaủ
HÌNH H C 12 Ọ
CH NG IIIƯƠ
PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ
I. KI N TH C C N NHẾ Ứ Ầ Ớ
1. H t a đ trong không gianệ ọ ộ :
a) H t a đ trong không gianệ ọ ộ :
oH g m ba tr c ệ ồ ụ
, ,O x O y O z
đôi m t vuông góc đ c g i là h tr c t a đ vuôngộ ượ ọ ệ ụ ọ ộ
góc trong không gian.
oN u ta l y ba vect đ n v ế ấ ơ ơ ị
, ,i j k
r ur ur
l n l t n m trên ầ ượ ằ
, ,O x O y O z
thì
2 2 2
1i j k= = =
r ur ur
và
. . . 0i j jk k i= = =
r ur ur ur ur r
.
b) T a đ c a vect và c a đi mọ ộ ủ ơ ủ ể :
o
( )
; ;u x y z u xi y j zk= + +�
r r r ur ur
.
o
( )
; ;M x y z O M xi y j zk= + +�uuuur r ur ur
.
oN u ế
( ) ( )
; ; & ; ;
A A A B B B
A x y z B x y z
thì
.
c) Vect b ng nhau. T a đ c a vect t ng, vect hi uơ ằ ọ ộ ủ ơ ổ ơ ệ : Cho
( ) ( )
1 1 1 2 2 2
; ; & ; ;u x y z v x y z
r r
. Khi đó:
o
1 2
1 2
1 2
x x
u v y y
z z
z=
=
= =��
�=
=
r r
.
o
( )
1 2 1 2 1 2
; ;u v x x y y z zu =xxy
r r
.
o
( )
1 1 1
; ;ku kx ky kz=
r
,
k∀ ∀
.
d) Hai vect cùng ph ngơ ươ :
Hai vect ơ
( ) ( )
1 1 1 2 2 2
; ; & ; ;u x y z v x y z
r r
cùng ph ng ươ
( )
0u u
r r
:k v ku∃ =� � r r
r
, t c là ứ
2 1
2 1
2 1
x kx
y ky
z kz
z=
==
=
==
=
hay
2 2 2
1 1 1
x y z
x y z
= =
.
e) Tích vô h ng c a hai vectướ ủ ơ : Cho
( ) ( )
1 1 1 2 2 2
; ; & ; ;u x y z v x y z
r r
. Khi đó:
o
( )
1 2 1 2 1 2
. . . os ,uv u v c u v x x y y z z= = + +
r r r r r r
.
o
22 2 2
1 1 1
u u x y z= = + +
r r
.
o
( ) ( ) ( )
2 2 2
B A B A B A
A B A B x x y y z z= = − + − + −
uuur
.
o
( )
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
os , .
x x y y z z
c u v
x y z x y z
+ +
=+ + + +
r r
.
o
1 2 1 2 1 2
0u v x x y y z z⊥ + + =�
r r
.
f) Tích có h ng c a hai vectướ ủ ơ : Trong không gian
O xyz
, cho hai vect ơ
( )
1 1 1
; ;u x y z
r
và
( )
2 2 2
; ;v x y z
r
.
HH12 – PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ Page 1 of 14
Gv: Lê Minh Gi yấ THPT Th Khoa Nghĩaủ
oTích có h ng c a hai vect ướ ủ ơ
&u v
r r
, kí hi u là ệ
,u v
� �
� �
r r
, đ c xác đ nh b i:ượ ị ở
1 1 1 1 1 1
2 2 2 2 2 2
, ; ;
y z z x x y
u v y z z x x y
� �
� �
=� �
� � � �
� �
r r
.
o
, , ,u v u u v v
� � � �
⊥ ⊥
� � � �
r r r r r r
.
o
( )
, . .sin ,u v u v u v
� �
=
� �
r r r r r r
.
o
&u v
r r
cùng ph ng khi và ch khi ươ ỉ
, 0u v
� �
=
� �
r r r
.
oBa vect ơ
, ,wu v
r r ur
đ ng ph ng ồ ẳ
, . 0u v w
� � =�� �
r r ur
.
g) Các ng d ng c a tích có h ngứ ụ ủ ướ :
oDi n tích tam giác: ệ
1,
2
A BC
S A B A C
� �
=� �
uuur uuuur
.
oTh tích kh i h p: ể ố ộ
. ' ' ' '
, .
ABCD A B C D
V A B A C A D
� �
=� �
uuur uuuur uuuur
.
oTh tích t di n: ể ứ ệ
1, .
6
A BC D
V A B A C A D
� �
=� �
uuur uuuur uuuur
.
h) M t c uặ ầ :
oM t c u tâm ặ ầ
( )
; ;I a b c
, bán kính
R
có ph ng trình là:ươ
( ) ( ) ( )
2 2 2 2
x a y b z c R− + − + − =
.
oPh ng trình ươ
2 2 2
2 2 2 0x y z ax by cz d+ + + + + + =
, v i ớ
+ + >
2 2 2
a b c d
, là
ph ng trình c a m t c u có tâm ươ ủ ặ ầ
( )
; ;I a b c− − −
và bán kính
2 2 2
R a b c d= + + −
.
2. Ph ng trình m t ph ng: ươ ặ ẳ
a) Vect pháp tuy n c a m t ph ngơ ế ủ ặ ẳ
o
0n n
ur r
đ c g i là vect pháp tuy n c a m t ph ng ượ ọ ơ ế ủ ặ ẳ
( )
α
n u giá c a ế ủ
n
ur
vuông góc
v i ớ
( )
α
, vi t t t là ế ắ
( )
n
α
⊥
ur
.
oN u hai vect ế ơ
( ) ( )
1 1 1 2 2 2
; ; & ; ;u x y z v x y z
r r
không cùng ph ng và giá c a chúngươ ủ
song song ho c n m trên ặ ằ
( )
α
thì vect ơ
1 1 1 1 1 1
2 2 2 2 2 2
, ; ;
y z z x x y
n u v y z z x x y
� �
� �
= = � �
� � � �
� �
ur r r
là m tộ
vect pháp tuy n c a ơ ế ủ
( )
α
.
b) Ph ng trình m t ph ng qua đi m và có vect pháp tuy nươ ặ ẳ ể ơ ế : M t ph ng qua đi mặ ẳ ể
( )
0 0 0
; ;M x y x
và có vect pháp tuy n ơ ế
( )
; ;n A B C
ur
có ph ng trình t ng quát làươ ổ
( ) ( ) ( )
0 0 0
0A x x B y y C z z− + − + − =
.
c) Ph ng trình t ng quát c a m t m t ph ngươ ổ ủ ộ ặ ẳ có d ng ạ
0A x By Cz D+ + + =
, v iớ
222
0A B C+ +C
. Khi đó,
( )
; ;n A B C
ur
là m t vect pháp tuy n c a m t ph ng đó.ộ ơ ế ủ ặ ẳ
d) Các tr ng h p đ c bi t c a ph ng trình t ng quát c a m t ph ngườ ợ ặ ệ ủ ươ ổ ủ ặ ẳ
Xét m t ph ng ặ ẳ
( )
α
có ph ng trình ươ
0A x By Cz D+ + + =
. Khi đó:
o
( )
0D
α
=
qua g c t a đ .ố ọ ộ
o
( )
0, 0C D
α
=D0
song song v i tr c ớ ụ
O z
.
HH12 – PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ Page 2 of 14
Gv: Lê Minh Gi yấ THPT Th Khoa Nghĩaủ
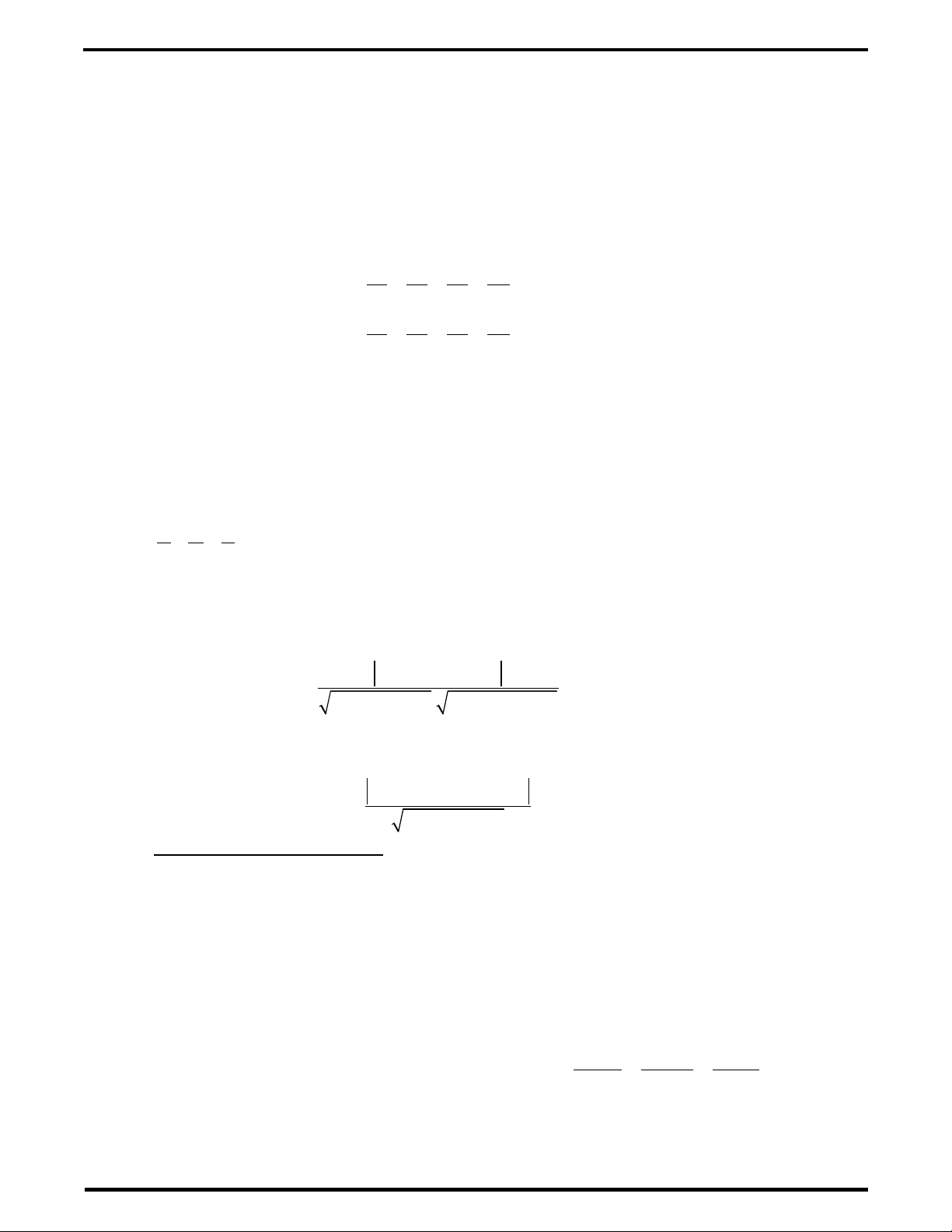
o
( )
0C D
α
= =
ch a tr c ứ ụ
O z
.
o
( )
0, 0B C D
α
= =D
song song v i ớ
( )
O yz
.
o
( )
0B C D
α
= = =
chính là
( )
O yz
.
oCác tr ng h p khác t ng t ……ườ ợ ươ ự
e) V trí t ng đ i c a hai m t ph ngị ươ ố ủ ặ ẳ .
Cho hai m t ph ng ặ ẳ
( )
: 0A x By Cz D
α
+ + + =
và
( )
' : ' ' ' ' 0A x B y C z D
α
+ + + =
.
Khi đó:
o
( ) ( )
α α
= = =� �' ' ' ' '
A B C D
A B C D
.
o
( ) ( )
α α
= =� �/ / ' ' ' ' '
A B C D
A B C D
.
o
( )
α
c t ắ
( )
'
α
۹ : : ': ': 'A B C A B C
.
o
( ) ( )
α α
⊥ + + =�' ' ' ' 0A A BB CC
.
f) Ph ng trình m t ph ng theo đo n ch nươ ặ ẳ ạ ắ .
M t ph ng ặ ẳ
( )
α
không qua g c t a đ , c t tr c ố ọ ộ ắ ụ
, ,O x O y O z
l n l t t iầ ượ ạ
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0;A a B b C c
, có ph ng trình theo đo n ch n là:ươ ạ ắ
( )
1 0
x y z abc
a b c
+ + =b
.
g) Góc gi a hai m t ph ngữ ặ ẳ
Cho hai m t ph ng ặ ẳ
( ) ( )
: 0 & ' : ' ' ' ' 0A x By Cz D A x B y C z D
α α
+ + + = + + + =
.
G i ọ
ϕ
là góc gi a hai m t ph ng ữ ặ ẳ
( ) ( )
& '
α α
,
khi đó:
2 2 2 2 2 2
'''
cos . ' ' '
A A BB CC
A B C A B C
ϕ
+ +
=+ + + +
.
h) Kho ng cách t m t đi m t i m t m t ph ngả ừ ộ ể ớ ộ ặ ẳ .
Cho
( )
: 0A x By Cz D
α
+ + + =
và đi m ể
( )
0 0 0
; ;M x y z
.
Khi đó:
( )
( )
α
+ + +
=+ +
0 0 0
222
,A x By Cz D
d M
A B C
.
3. Ph ng trình đ ng th ng:ươ ườ ẳ
a) Ph ng trình đ ng th ng qua m t đi m và có m t vect ch ph ngươ ườ ẳ ộ ể ộ ơ ỉ ươ
Đ ng th ng d qua ườ ẳ
( )
0 0 0
; ;M x y z
và có vect ch ph ng ơ ỉ ươ
( )
; ;u a b c
r
. Khi đó:
oĐ ng th ng d có ph ng trình tham s là ườ ẳ ươ ố
0
0
0
x x at
y y bt
z z ct
z= +
== +
=
== +
=
.
oN u ế
M dM
thì
( )
0 0 0
; ;M x at y bt z ct+ + +
.
oĐ ng th ng d có ph ng trình chính t c là ườ ẳ ươ ắ
0 0 0
, 0
x x y y z z abc
a b c
− − −
= =−
.
b) Đ ng th ng giao tuy n c a hai m t ph ngườ ẳ ế ủ ặ ẳ
HH12 – PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ Page 3 of 14
Gv: Lê Minh Gi yấ THPT Th Khoa Nghĩaủ
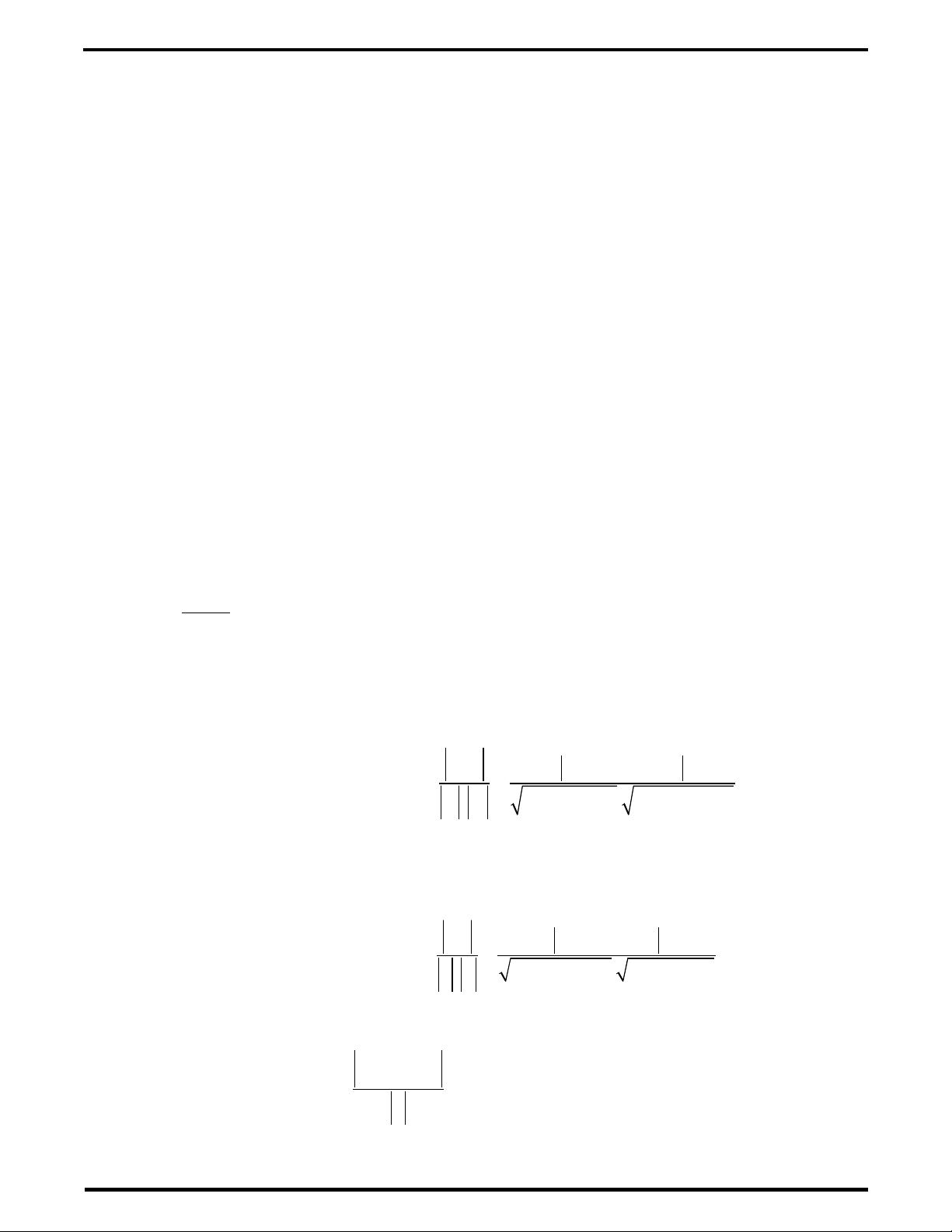
Cho hai m t ph ng ặ ẳ
( ) ( )
: 0 & ' : ' ' ' ' 0A x By Cz D A x B y C z D
α α
+ + + = + + + =
v iớ
đi u ki n ề ệ
: : ': ': 'A B C A B C
A
. G i ọ
( ) ( )
'd
α α
=α
.
Khi đó m t vect ch ph ng c a d là ộ ơ ỉ ươ ủ
, 'u n n
� �
=� �
r ur uur
v i ớ
( ) ( )
; ; & ' '; '; 'n A B C n A B C
ur uur
.
c) V trí t ng đ i gi a hai đ ng th ngị ươ ố ữ ườ ẳ
Cho hai đ ng th ng ườ ẳ
1
d
qua
1
M
có vect ch ph ng ơ ỉ ươ
1
u
ur
và
2
d
qua
2
M
và có vectơ
ch ph ng ỉ ươ
2
u
uur
. Khi đó:
o
1 2
&d d
cùng n m trong m t m t ph ng ằ ộ ặ ẳ
1 2 1 2
, . 0u u M M
� � =�� �
ur uur uuuuuuur
.
o
1 2
1 2
1 1 2
, 0
, 0
u u
d d
u M M
u� �
=
=� �
�M�
� �
=
=� �
�
ur uur r
ur uuuuuuur r
.
o
1 2
1 2
1 1 2
, 0
/ / , 0
u u
d d
u M M
u� �
=
=� �
��
� �
�
�
� �
�
ur uur r
ur uuuuuuur r
.
o
1 2
&d d
c t nhau ắ
1 2 1 2
1 2
, . 0
, 0
u u M M
u u
u� � =
=� �
�
� �
�
�
� �
�
ur uur uuuuuuur
ur uur r
.
o
1 2
&d d
chéo nhau
1 2 1 2
, . 0u u M M
� �
۹� �
ur uur uuuuuuur
.
L u ýư: Có th xét v trí t ng đ i c a hai đ ng th ng b ng cách gi i h ph ng trìnhể ị ươ ố ủ ườ ẳ ằ ả ệ ươ
đ tìm giao đi m c a hai đ ng th ng (n u có và xét thêm ph ng c a chúng trongể ể ủ ườ ẳ ế ươ ủ
tr ng h p h vô nghi m).ườ ợ ệ ệ
d) Góc gi a hai đ ng th ngữ ườ ẳ
Cho hai đ ng th ng ườ ẳ
1 2
,d d
l n l t có vect ch ph ng ầ ượ ơ ỉ ươ
( ) ( )
1 1 1 1 2 2 2 2
, , & , ,u a b c u a b c
ur uur
.
G i ọ
ϕ
là góc gi a ữ
1 2
&d d
.
Khi đó,
0
0 90
ϕ
ϕ9
và
1 2 1 2 1 2 1 2
2 2 2 2 2 2
1 2 1 1 1 2 2 2
.
os ..
u u aa bb cc
c
u u a b c a b c
ϕ
+ +
= = + + + +
ur uur
ur uur
.
e) Góc gi a đ ng th ng và m t ph ngữ ườ ẳ ặ ẳ
Cho đ ng th ng ườ ẳ
d
có vect ch ph ng ơ ỉ ươ
( )
; ;u a b c
r
và
( )
α
có vect pháp tuy nơ ế
( )
; ;n A B C
ur
. G i ọ
ϕ
là góc gi a ữ
( )
&d
α
.
Khi đó,
0
0 90
ϕ
ϕ9
và
2 2 2 2 2 2
.Aa
sin ..
u n Bb Cc
u n A B C a b c
ϕ
+ +
= = + + + +
r ur
r ur
.
f) Kho ng cách t m t đi m đ n m t đ ng th ngả ừ ộ ể ế ộ ườ ẳ
Cho đi m ể
1
M
, đ ng th ng ườ ẳ
∆
qua
0
M
và có vect ch ph ng ơ ỉ ươ
u
r
.
Khi đó
( )
1 0
1
,
,M M u
d M
u
� �
� �
∆ =
uuuuuuur r
r
.
g) Kho ng cách gi a hai đ ng th ng chéo nhauả ữ ườ ẳ .
HH12 – PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ Page 4 of 14
Gv: Lê Minh Gi yấ THPT Th Khoa Nghĩaủ
Cho hai đ ng th ng chéo nhau: ườ ẳ
1
∆
qua
1
M
có vect ch ph ng ơ ỉ ươ
1
u
ur
và
2
∆
qua
2
M
có vect ch ph ng ơ ỉ ươ
2
u
uur
. Khi đó
( )
1 2 1 2
1 2
1 2
, .
,,
u u M M
d
u u
� �
� �
∆ ∆ = � �
� �
ur uur uuuuuuur
ur uur
.
II. CÁC BÀI TOÁN C B NƠ Ả
1. Cho ba vect ơ
( ) ( ) ( )
2; 5;3 , 0;2; 1 , 1;7;2a b c− −
r r r
:
a) Tính t a đ c a vect ọ ộ ủ ơ
1
4 3
3
u a b c= − +
r r r r
b) Tính t a đ c a vect ọ ộ ủ ơ
4 2v a b c= − −
r r r r
2. Cho hình h p ộ
. ' ' ' 'A BCD A B C D
bi t ế
( ) ( ) ( ) ( )
1;0;1 , 2;1;2 , 1; 1;1 , ' 4;5; 5A B D C− −
. Tính
t a đ các đ nh còn l i c a hình h p.ọ ộ ỉ ạ ủ ộ
3. Tìm t a đ tâm và bán kính m i m t c u có ph ng trình sau đây:ọ ộ ỗ ặ ầ ươ
a)
2 2 2
8 2 1 0x y z x y+ + − − + =
b)
2 2 2
9 9 9 6 18 1 0x y z x z+ + − + + =
.
4. L p ph ng trình c a m t c u ậ ươ ủ ặ ầ
( )
S
trong các tr ng h p sau:ườ ợ
a)
( )
S
có đ ng kính ườ
A B
v i ớ
( ) ( )
6;4; 3 & 2;8;1A B−
.
b)
( )
S
có tâm thu c ộ
O z
và đi qua hai đi m ể
( ) ( )
0;1;2 & 1;0; 1M N −
5. Cho b n đi m ố ể
( ) ( ) ( ) ( )
1;0;0 , 0;1;0 , 0;0;1 , 2;1; 2A B C D − −
.
a) Ch ng minh r ng ứ ằ
, , ,A B C D
là b n đ nh c a m t t di n.ố ỉ ủ ộ ứ ệ
b) Tính góc t o b i các c nh đ i c a t di n đóạ ở ạ ố ủ ứ ệ .
c) Tính th tích t di n ABCDể ứ ệ .
d) Tính đ dài đ ng cao c a t di n ABCD k t đ nh A.ộ ườ ủ ứ ệ ẻ ừ ỉ
6. Cho các vect ơ
( ) ( ) ( )
1;0; 2 , 1;2; 1 , 0;3; 2abc−−−
r r r
. Tìm t a đ c a ọ ộ ủ
u
r
bi t:ế
a)
2 3 2 0a b c u+ − − =
r r r r r
.
b)
, & 21u a u b u⊥ ⊥ =
r r r r r
.
7. Cho các đi m ể
( ) ( ) ( )
1;2; 1 , 2; 1;3 , 2;3;3A B C− − −
.
a) Ch ng minh ứ
, ,A B C
là ba đ nh c a m t tam giác.ỉ ủ ộ
b) Tìm t a đ c a đi m ọ ộ ủ ể
M
là đ nh th t c a hình bình hành ỉ ứ ư ủ
A BCM
.
c) Tìm t a đ các đi m t ng ng là chân đ ng phân giác trong, ngoài c a góc ọ ộ ể ươ ứ ườ ủ
A
c a ủ
A BC∆
.
d) Ch ng minh ứ
, , ,O A B C
là b n đ nh c a m t t di n. Tìm t a đ tr ng tâm c a tố ỉ ủ ộ ứ ệ ọ ộ ọ ủ ứ
di n đó.ệ
8. Cho các đi m ể
( ) ( ) ( )
2;1; 2 , 3;0;1 , 2; 1;3 ,A B C D O y− −C
.
a) Tính di n tích ệ
A BC
∆
.
b) Tính đ dài đ ng cao k t đ nh ộ ườ ẻ ừ ỉ
A
c a ủ
A BC∆
.
c) Tìm t a đ đi m ọ ộ ể
D
sao cho t di n ứ ệ
A BCD
có th tích b ng 5.ể ằ
d) Tính góc gi a đ ng th ng ữ ườ ẳ
&BC O A
.
9. Hãy vi t ph ng trình m t c u trong m i tr ng h p sau:ế ươ ặ ầ ỗ ườ ợ
a) Đi qua
( )
5; 2;1A−
và có tâm
( )
3; 3;1K−
.
HH12 – PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ Page 5 of 14