
HÌNH HỌC
TÓM TẮT LÝ THUYẾT
I) PHÉP CỘNG – TRỪ CÁC VÉC TƠ
1) Một số quy tắc – Tính chất áp dụng trong phép công trừ các véc tơ
Quy tắc ba điểm : với ba điểm A, B, C bất kỳ ta có :
*
AB BC AC
* ACBABC
Quy tắc hình bình hành : ABCD là hbh ta có :
AB AD AC
Trung điểm của đoạn thẳng :
I là trung điểm của đoạn AB , với điểm M tuỳ ý ta luôn có :
* 0 IBIA
*
IM
MB
MA
2
Trọng tâm của tam giác :
G là trọng tâm của ABC
0
GA GB GC
G là trọng tâm của ABC với điểm M tuỳ ý ta luôn có :

3
MA MB MC MG
2) Tính chất : Cho ba véc tơ
a
,
b
và
c
ta có :
a
+
0
=
0
+
a
=
a
(Tính chất của véc tơ – không )
a
+
b
=
b
+
a
(Tính chất giao hoán )
(
a
+
b
) +
c
=
a
+ (
b
+
c
) ( tính chất kết hợp )
II) PHÉP NHÂN MỘT VÉC TƠ VỚI MỘT SỐ
1) Định nghĩa : Tích số k với một véc tơ
a
là một véc tơ là một số thực
kí hiệu : k
a
thỏa :
Cùng hướng với véc tơ
a
nếu k 0
Ngược hướng với véc tơ
a
nếu k > 0
Có độ dài bằng k
a
2) Tính chất : Với mọi véc tơ
a
và mọi số thực k. l ta có :
k(l
a
) = (k.l)
a
(k + l)
a
= k
a
+ l
a

k(
a
+
b
) = k
a
+ k
b
1.
a
=
a
; 0.
a
=
0
; k.
0
=
0
3) Véc tơ cùng phương : hai véc tơ
a
và
b
cùng phương (
a
0
) thì
có một số thực k duy nhất sao cho
b
= k
a
4) Ba điểm thẳng hàng :
Ba điểm A , B , C thẳng hàng ACkABk :
5) Phân tích 1 véc tơ theo hai véc tơ không cùng phương :
Cho
a
và
b
không cùng phương . luôn có duy nhất cặp số thực k , l sao cho
blakx
III) HỆ TRỤC TỌA ĐỘ ĐÊCAC VUÔNG GÓC
1) Tọa độ của véc tơ :
Định nghĩa:
u
= (x ; y)
u
= x
i
+ y
j
Tính chất: Trong mp(Oxy) cho
u
= (x ; y) ,
v
= (x’; y’) ta có :
'
'
yy
xx
vu

u
+
v
= (x + x’ ; y + y’)
u
-
v
= (x – x’ ; y – y’)
k
u
= (kx ; ky)
2) Tọa độ của một điểm :
Định nghĩa: M(x ; y)
OM
= x
i
+ y
j
Tính chất:
Trong mp(Oxy) cho hai điểm A(xA ; yA) và B(xB; yB) ta có :
Véc tơ :
AB
= (xB– xA ; yB– yA)
Trung điểm I của đoạn AB : 2
2
A B
I
A B
I
x x
x
y y
y
Toạ độ trọng tâm G của ABC :
3
3
CBA
G
CBA
G
yyy
y
xxx
x
IV).GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ
1) ĐỊNH NGHĨA :
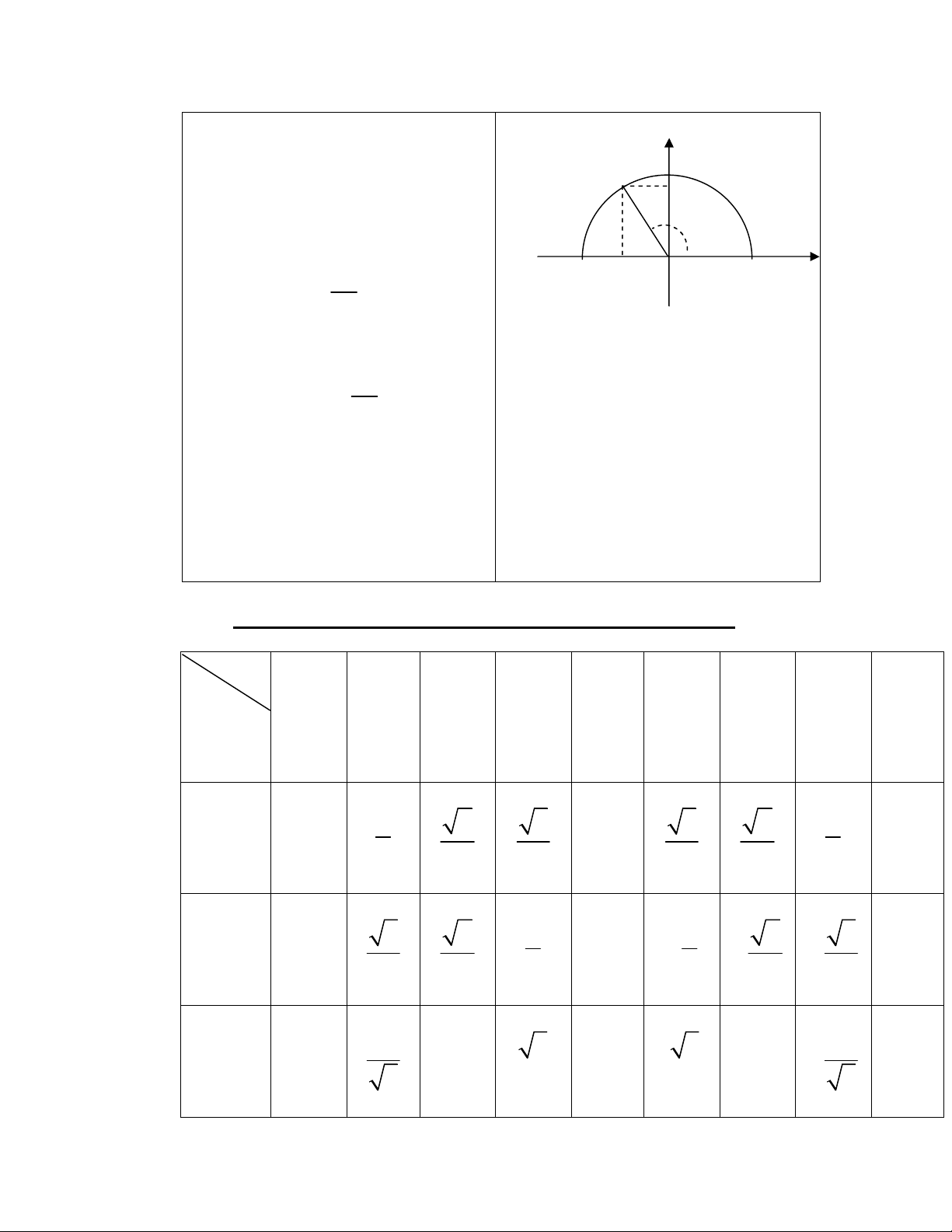
sin = y0
cos = x0
tg =
0
0
y
x
( x0 0 )
cotg =
0
0
x
y
( y0 0 )
y
M(x0 ; y0) B
y0
A’ x0
O A
x
2) TỈ SỐ LƯỢNG GIÁC MỘT SỐ GÓC THƯỜNG DÙNG :
Độ
HSLG
0o 30o 45o 60o 90o 120o 135o 150o 180o
Sin 0
1
2
2
2
3
2
1
3
2
2
2
1
2
0
Cos 1
3
2
2
2
1
2
0
1
2
2
2
3
2
-1
Tg 0
1
3
1
3
-
3
-1
1
3
0


























