KHAI THÁC M I QUAN H GI A HÌNH H C KHÔNG GIAN VÀỐ Ệ Ữ Ọ
HÌNH H C PH NG TRONG GI NG D Y TOÁN THPTỌ Ẳ Ả Ạ Ở
===================================
A. ĐT V N ĐẶ Ấ Ề :
Trong quá trình d y và h c toán, đi v i h c sinh ph thông th ngạ ọ ố ớ ọ ổ ườ
chúng ta ph i phân tích , phán đoán các h ng gi i quy t bài toán, liên hả ướ ả ế ệ
gi a bài toán đó v i các bài toán quen thu c, đn gi n h n đ có h ng gi iữ ớ ộ ơ ả ơ ể ướ ả
quy t t ng t , ng c l i đi v i các h c sinh khá, gi i chúng ta l i có thế ươ ự ượ ạ ố ớ ọ ỏ ạ ể
t m t bài toán đn gi n đi sâu phân tích, m r ng, phát tri n thành nh ng bàiừ ộ ơ ả ở ộ ể ữ
toán m i. Đc bi t trong ch ng trình hình h c THPT, vi c khai thác đcớ ặ ệ ươ ọ ở ệ ượ
các liên h gi a không gian hai chi u ( hình h c ph ng: T ng h p và t a đ)ệ ữ ề ọ ẳ ổ ợ ọ ộ
và không gian ba chi u ( hình h c không gian: T ng h p và t a đ) giúp h cề ọ ổ ợ ọ ộ ọ
sinh gi i quy t đc nhi u v n đ toán h c phù h p v i nhi u đi t ngả ế ượ ề ấ ề ọ ợ ớ ề ố ượ
h c sinh, v i nhi u m c đ ki n th c khác nhau,n i dung ki n th c này đcọ ớ ề ứ ộ ế ứ ộ ế ứ ượ
xu t hi n khá nhi u trong các kì thi: Kh o sát ch t l ng, thi H c sinh gi iấ ệ ề ả ấ ượ ọ ỏ
các c p, thi H c sinh gi i Qu c gia,.... Vi c s d ng ph ng pháp gi i điấ ọ ỏ ố ệ ử ụ ươ ả ố
v i m t bài toán hình h c ph ng đ gi i m t bài toán hình h c không gianớ ộ ọ ẳ ể ả ộ ọ
t ng t và m r ng m t s bài toán ph ng sang bài toán trong không gianươ ự ở ộ ộ ố ẳ
m i s giúp ho t đng gi ng d y và h c t p môn hình h c đt hi u qu caoớ ẽ ạ ộ ả ạ ọ ậ ọ ạ ệ ả
h n.ơ
B. M T S VÍ D MINH H AỘ Ố Ụ Ọ
Bài toán 1:
Trên m t ph ng to đ ặ ẳ ạ ộ xOy cho đi m ểA(2;0), B(1;3). Tìm to đ c aạ ộ ủ
đi m ểM trên đng th ng 4ườ ẳ x + y - 9 = 0 sao cho kho ng ảMA + MB nh nh t.ỏ ấ
Bài toán 1':
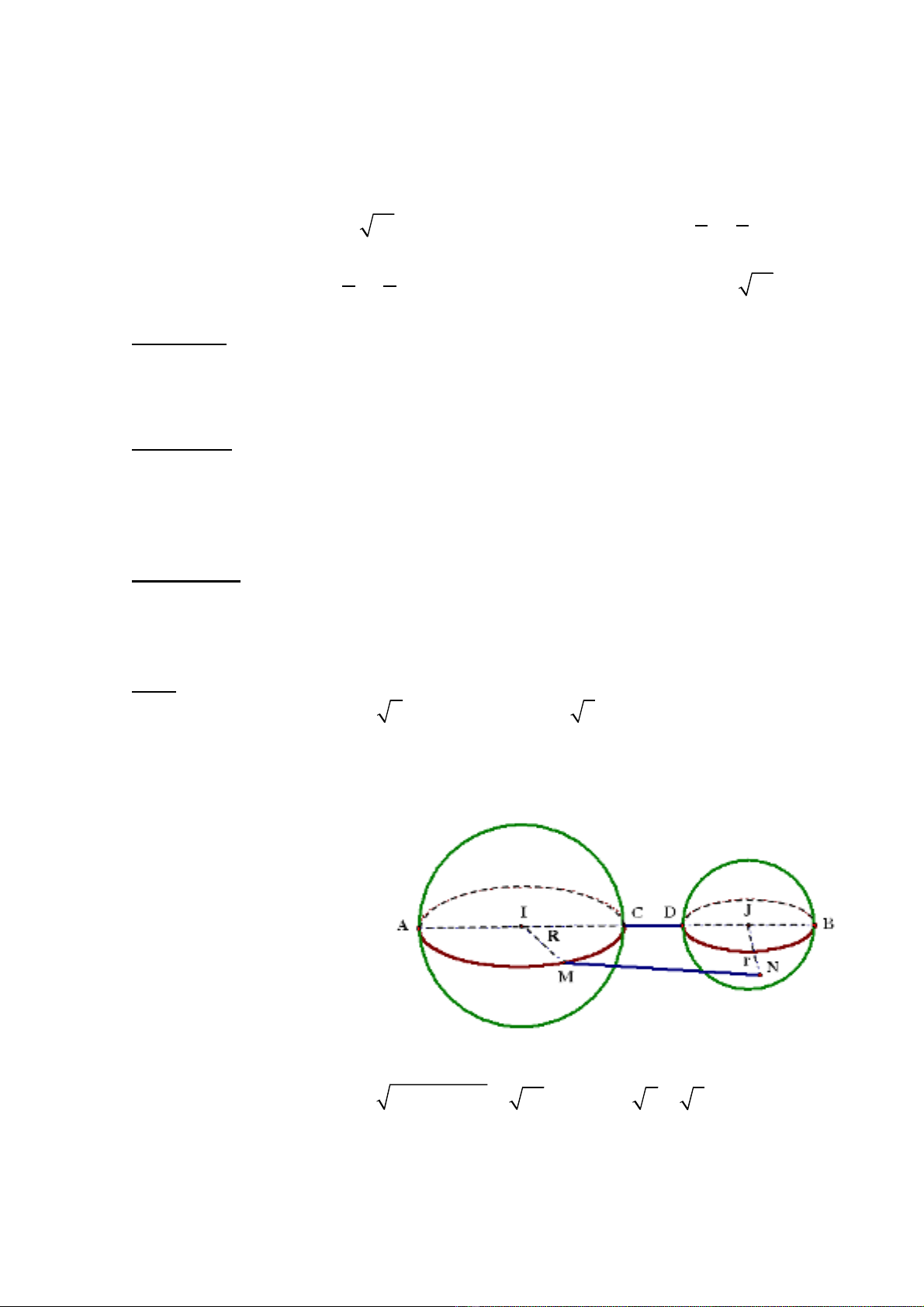
Cho
( ) ( ) ( )
2 2 2
2 2 2
2 2 1S x y z x y z= + + + + + − + −
, trong đó x , y , z
là các s th c thay đi nh ng luôn tho mãn ố ự ổ ư ả
3 0x y z+ + − =
. Tìm giá tr nh ị ỏ
nh t c a bi u th c ấ ủ ể ứ S.
Nh n xét 1ậ: V i các cách nhìn khác nhau, bài toán 1 khá quen thu c v i h cớ ộ ớ ọ
sinh t ti u h c tr lên và có nhi u cách gi i, ta đ ý cách gi i b ng hình h cừ ể ọ ở ề ả ể ả ằ ọ
có th v n d ng vào không gian đ gi i bài toán 1' nên ta có th gi i bài toánể ậ ụ ể ả ể ả
này nh sau: ư
Gi i ả: Trong h tr c to đ Đ Cácệ ụ ạ ộ ề
vuông góc Oxyz, xét các đi mể
( ) ( )
0;0;0 , 2;2;1O A −
và m t ph ngặ ẳ
( )
: 0P x y z+ + =
. D th y ễ ấ O và A
n m cùng phía v i nhau đi v i (ằ ớ ố ớ P) .
1
G i ọB là đi m đi x ng c a ể ố ứ ủ O qua (P), V i m i đi m ớ ỗ ể M(x;y;z) (P) ta luôn
có MO = MB và S =MO + MA AB (Không đi ). D u "=" x y ra ổ ấ ả M I
Trong đó I = AB(đo n)ạ
(P), khi đó S đt giá tr nh nh t. Tìm to đ c a ạ ị ỏ ấ ạ ộ ủ B
ta đc ượ B(2;2;2)
17AB =
. Tìm t a đ đi m ọ ộ ể I ta đc ượ
2 7
;2;
5 5
I� �
−
� �
� �
nên v iớ
c p giá tr ặ ị
( )
2 7
; ; ;2;
5 5
x y z � �
= −
� �
� �
ta có S đt giá tr nh nh t là ạ ị ỏ ấ
min
17S=
.
Bài toán 2:
Cho
2 2
2 2 1 0x y x y+ + − + =
và
v i ớx, y, z, t là
các s th c thay đi. ố ự ổ Tìm Max, min c a bi u th c ủ ể ứ
( ) ( )
2 2
S x t y z= − + −
.
Bài toán 2':
Cho
2 2 2
2 2 4 4 0x y z x y z+ + + − + + =
;
2 2 2
2 2 1 0a b c b c+ + + − − =
,
trong đó x , y , z , a , b , c là các s th c thay đi. Tìm Max, min c a bi u th cố ự ổ ủ ể ứ
( ) ( ) ( )
2 2 2
S x a y b z c= − + − + −
.
Nh n xét 2ậ: V i cách nhìn nh n bài toán 2 d i góc đ hình h c ta có ớ ậ ướ ộ ọ S là
bình ph ng kho ng cách gi a hai đi m ươ ả ữ ể M(x;y) và N(t;z) khi M,N thay điổ
trên hai đng tròn c đnh, ta có cách nhìn nh n bài toán 2' d i góc đườ ố ị ậ ướ ộ
t ng t nên có th đa l i gi i c a bài toán 2' nh sau:ươ ự ể ư ờ ả ủ ư
Gi iả : Trong h tr c to đ Đ Các vuông góc ệ ụ ạ ộ ề Oxyz xét các m t c u (ặ ầ I;R) và
(J;r) có tâm I(-1;1;-2) ,
R=2
và J(0;-1;1) ,
r=3
.
( ) ( ) ( ) ( )
2 2 2
; : 1 1 2 2I R x y z+ + − + + =
2 2 2
2 2 4 4 0x y z x y z+ + + − + + =
(I)
( ) ( ) ( )
2 2
2 2 2 2
; : 1 1 3 2 2 1 0J r x y z x y z y z+ + + − = + + + − − =�
(J)
T gi thi t ta có ừ ả ế
( ) ( )
; ;M x y z I
,
( ) ( )
, ; ;N a b c J
.
D th yễ ấ
2
,S MN=
2 3d IJ R r= = + + = > + = +
2 2 2
1 2 3 14
nên 2 m t ặ
c u trên ngoài nhau ầ S đt Max , min ạ MN đt Max , min.ạ
Khi M thay đi trên (ổI) , N thay đi trên (ổJ) thì:
2
14 2 3
Max
MN AB d R r= = + + = + +
( )
2
14 2 3
Max
S= + +
min
14 2 3MN CD d R r= = − − = − −
( )
2
min
14 2 3S= − −
.
Bài toán 3:
Cho ABC là tam giác vuông t i A , v i đ dài các c nh là ạ ớ ộ ạ a , b , c ;
đng cao ườ AH = h ; b' = CH, c' = BH ; , là góc gi a m t đng th ngữ ộ ườ ẳ
b t kì v i hai đng th ng ấ ớ ườ ẳ AB , AC t ng ng thì ta luôn có các h th c : ươ ứ ệ ứ
a)
2 2 2 2
',b ab b c a= + =
b)
2 2 2
1 1 1
h b c
= +
c)
2 2
cos cos 1
α β
+ =
.
Bài toán 3':
Cho OABC là t di n vuông đnh ứ ệ ỉ O , đng cao ườ OH = h , OA = a , OB =
b , OC = c ; g i ọS , SA , SB , SC th t là di n tích các tam giác ứ ự ệ ABC , OBC ,
OCA , OAB ; S'A , S'B , S'C th t là di n tích các tam giác ứ ự ệ HBC , HCA , HAB
và , , th t là góc gi a m t đng th ng b t kì v i các đng th ngứ ự ữ ộ ườ ẳ ấ ớ ườ ẳ
OA , OB , OC . Ta luôn có :
a)
2 ' 2 2 2 2
. ,
A A A B C
S S S S S S S= = + +
b)
2 2 2 2
1 1 1 1
h a b c
= + +
c) cos2 + cos2 + cos2 = 1 .
Nh n xét 3ậ:
Bài toán 3 r t quen thu c v i h c sinh t l p 9 c v n i dung và cáchấ ộ ớ ọ ừ ớ ả ề ộ
gi i, v i cách nhìn m rông trong không gian ta có th đt v n đ v ki nả ớ ở ể ặ ấ ề ề ế
th c và cách ch ng minh m r ng c a bài toán 3 thành bài toán 3' m t cách dứ ứ ở ộ ủ ộ ễ
dàng, v n đ này SGK l p 11 cũng có các bài t p v v n đ này, ta có thấ ề ớ ậ ề ấ ề ể
đa v n đ và ch ng minh t ng t , ch ng h n t ng t ph n 3-c hìnhư ấ ề ứ ươ ự ẳ ạ ươ ự ầ ở
h c ph ng, v i các ch ng minh b ng véc t l p 10, ta ch ng minh 3'-c b ngọ ẳ ớ ứ ằ ơ ở ớ ứ ằ
ph ng pháp véc t nh sau:ươ ơ ư
Ch ng minh 3'- cứ :
Trên 3 c nh ạOA , OB , OC đt 3 véc t đnặ ơ ơ
v ị
1 2 3
, ,e e e
ur ur ur
nh hình v ( chúng có đ dàiư ẽ ộ
b ng 1 và đôi m t vuông góc );g i ằ ộ ọ
u
r
là véc
t ch ph ng cho ơ ỉ ươ , luôn có s bi u thự ể ị
duy nh t ấ
1 2 3
u xe y e z e= + +
r ur ur ur
3
Ta có
( )
12 2 2
x
u e
x y z
α
=+ +
r ur
cos cos ; =
( )
22 2 2
y
u e
x y z
β
=+ +
r ur
cos cos ; =
( )
32 2 2
z
u e
x y z
γ
=+ +
r ur
cos cos ; =
D dàng suy ra cosễ2 + cos2 + cos2 = 1 .
( Các bài t p 3'-a , 3'-b đã có h ng ch ng minh trong sách bài t p hình h c 11ậ ướ ứ ậ ọ
ho c có th ch ng minh b ng véc t )ặ ể ứ ằ ơ
Bài toán 4:
Ch ng minh trong tam giác ứABC b t kì, tr ng tâm ấ ọ G, tr c tâm ựH, tâm
đng tròn ngo i ti p ườ ạ ế O th ng hàng và ẳ
2GH GO=
(Đng th ng le). ườ ẳ Ơ
Bài toán 4’ :
Ch ng minh r ng, v i t di n tr c tâm ứ ằ ớ ứ ệ ự ABCD, ta luôn có: tr ng tâm ọG,
tr c tâm ựH và tâm O c a m t c u ngo i ti p t di n th ng hàng và ủ ặ ầ ạ ế ứ ệ ẳ GH = GO.
Nh n xét 4ậ: Trong nhi u cách ch ng minh bài toán 4, ta đ ý cách ch ngề ứ ể ứ
minh b ng phép v t nên ta có th nghĩ đn vi c dùng phép v t đ gi i bàiằ ị ự ể ế ệ ị ự ể ả
toán 4'. H n n a, trong không gian, không ph i t di n nào cũng có các đngơ ữ ả ứ ệ ườ
cao đng quy t i m t đi m nên ta ch xét nh ng t di n có tính ch t này (tồ ạ ộ ể ỉ ữ ứ ệ ấ ứ
di n tr c tâm).ệ ự
Gi iả:
Ta cũng s dùng phép v t đ gi i bài toán trong không gian. Yêu c uẽ ị ự ể ả ầ
ch ng minh ứGH = GO g i ý cho ta nghĩ đn phép v t tâm ợ ế ị ự G t s -1.ỉ ố
L n l t l y ầ ượ ấ A đi x ng v i ′ ố ứ ớ A, B đi x ng v i ′ ố ứ ớ B, C đi x ng v i ′ ố ứ ớ C,
D đi x ng v i ′ ố ứ ớ D qua G.
Ta d th y ễ ấ AA' //=AB
(tính ch t phép v t ) và đngấ ị ự ườ
trung bình EF (E,F th t làứ ự
trung đi m c a ể ủ CD và AB)
cũng đi qua G . Trong hình bình
hành A'B'AB E cũng là trung
đi m c a ể ủ A'B'
A'CB'D là
hình bình hành.
4
M t khác trong t di n tr c tâm ặ ứ ệ ự ABCD có hai c nh đi di n vuông gócạ ố ệ
v i nhau nên ớAB CD A'B' CD
A'CB'D là hình thoi
A'C = A'B.
Ch ng minh t ng t ta cũng có ứ ươ ự A'C = A'D A’ cách đu ềB, C, D.
nnnnn
T gi thi t ta cũng có ừ ả ế O cách đu ềB,C,D nên A'O là tr c c a đng trònụ ủ ườ
ngo i ti p ạ ế BCD A'O (BCD) A'O (B'C'D') (1).
T ng t (1), ta cũng có ươ ự B'O (A'C'D') (2); C'O (B'A'D') (3) O là tr cự
tâm c a t di n ủ ứ ệ A'B'C'D'.
Xét phép v t ị ự
1
G
V
−
, ta có:
1 ' ' '
: A , B, C , D
G
V A B C D
−
a a a a
Nh v y, ư ậ
1
: ( ) ( ' ' ' ')
G
V ABCD A B C D
−
a
nên phép v t s bi n tr c tâmị ự ẽ ế ự
c a t di n ủ ứ ệ ABCD thành tr c tâm ựO c a t di n ủ ứ ệ A’B’C’D’.
Suy ra:
1
:
G
V H O
−
a
hay
GO GH= −
uuur uuur
H, G, O th ng hàng và ẳGO = GH.
Bài toán 5:
Ch ng minh trong tam giác b t kì, 9 đi m g m: chân ba đng cao, baứ ấ ể ồ ườ
trung đi m c a ba c nh, ba trung đi m các đo n n i tr c tâm v i các đnhể ủ ạ ể ạ ố ự ớ ỉ
đu thu c m t đng tròn (Đng tròn le).ề ộ ộ ườ ườ Ơ
Bài toán 5’:
Cho t di n tr c tâm ứ ệ ự ABCD. G i ọ
1 2 3 4 1 2 3 4 1 2 3 4
, , , ; , , , ; , , ,H H H H G G G G I I I I
l n l t là chân 4 đng cao, tr ng tâm các m t và các đi m trên 4 đo nầ ượ ườ ọ ặ ể ạ
th ng n i tr c tâm v i các đnh th a mãn ẳ ố ự ớ ỉ ỏ
1 2 3 4
1 2 3 4
1
2
I H I H I H I H
I A I B I C I D
= = = =
. Ch ngứ
minh 12 đi m đó cùng thu c m t m t c u.ể ộ ộ ặ ầ
(t di n c n xét ph i có các đng cao đng quy nên là t di n tr cứ ệ ầ ả ườ ồ ứ ệ ự
tâm)
M t cách gi i bài toán 5ộ ả : Gi s tam giác ả ử ABC có H1, H2, H3, M1, M2, M3, I1,
I2, I3 l n l t là 3 chân 3 đng cao, 3 trung đi m 3 c nh, 3 trung đi m cácầ ượ ườ ể ạ ể
đo n n i tr c tâm v i các đnh. G i ạ ố ự ớ ỉ ọ E1,
E2, E3, F1, F2, F3 l n l t là các đi m điầ ượ ể ố
x ng v i ứ ớ H qua H1, H2, H3, M1, M2, M3. Dễ
dàng ch ng minh đc 9 đi m ứ ượ ể A, B, C,
H1, H2, H3, M1, M2, M3 cùng thu c đngộ ườ
tròn (S) ngo i ti p tam giác ạ ế ABC.
Ta có
1
2
H
V
:
1
A Ia
,
1 1
E Ha
,
1 1
F Ma
1 1 1
, ,I H M
thu c đng trònộ ườ
5
A'