Chương 3: Ma trận tán xạ
Trang 77
Chương 3
MA TRẬN TÁN XẠ
3.1 Khái niệm
Nội dung của chương này giới thiệu một phương cách mô hình hóa một mạch
điện hoặc một phần mạch điện ở tần số siêu cao bằng các phần tử tương đương
có thông số phân bố hoặc tập trung trung, biểu diễn dưới dạng các mạng nhiều
cửa . Thông số của mạng được định nghĩa thông qua các ma trận đặc tính . Biết
được giá trị của ma trận đó là biết được hoàn toàn đặc tính hoạt động của
mạng, mà ta không cần quan tâm đến cấu trúc thực tế của các phần tử trong
mạng , đến cường độ điện từ trường tại các điểm của mạng.
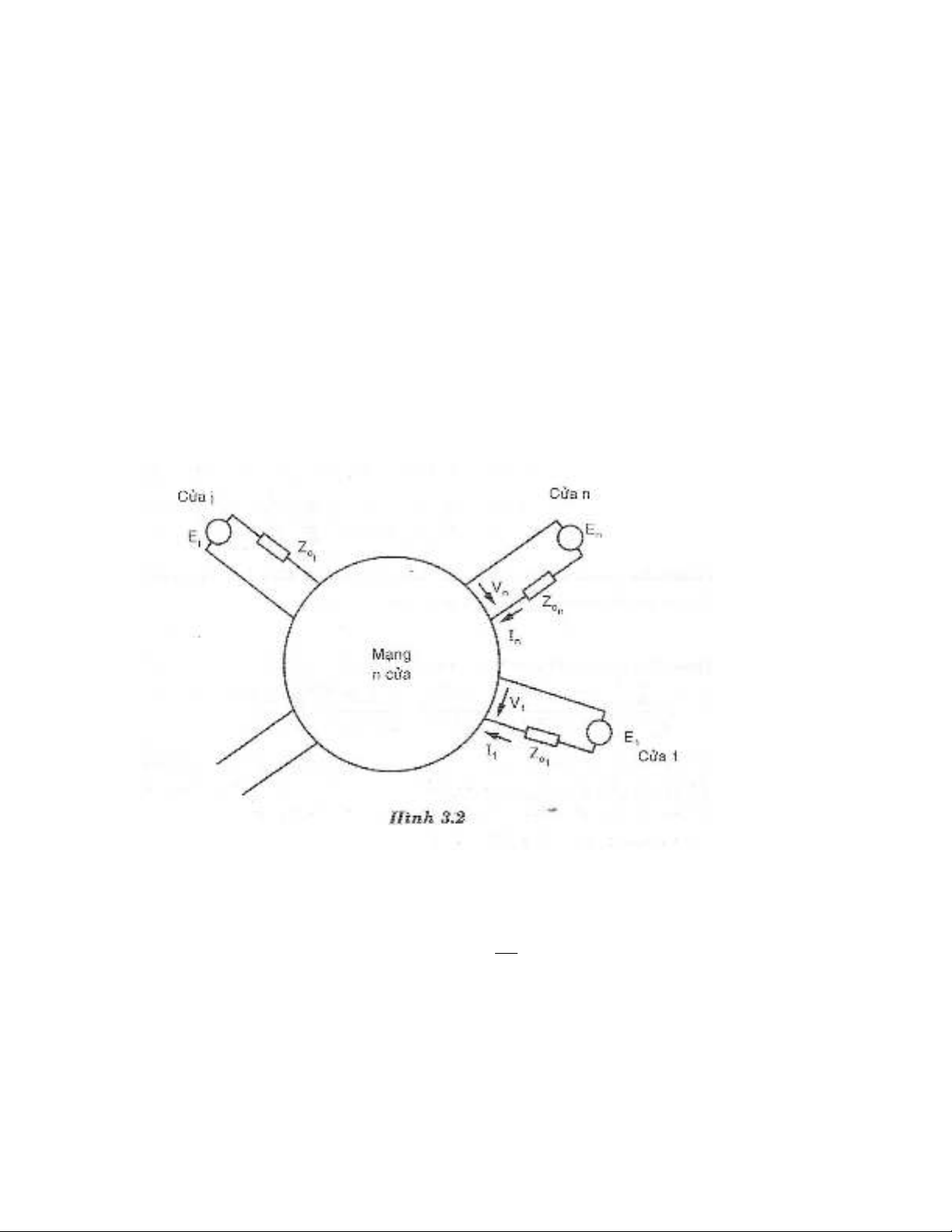
Hình 3.2 một mạng n cửa được đánh số từ cửa 1 đến cửa n. Tại mỗi cửa j , có
một nguồn tín hiệu EJ và một nội trở nguồn ZoJ (được chọn làm trở kháng
chuẩn cho cửa j đó)
Điện áp và dòng điện tại ngõ vào cửa j bất kỳ là tổng của sóng tới và sóng phản
xạ:
Vj = Vij + Vrj
Ij = Iij - Irj
nj ,1
3.2 Ma trận Tán Xạ
S
- các hệ số:
1. Dẫn dắt ban đầu
Chương 3: Ma trận tán xạ
Trang 78
Cho mạch điện đơn giản gồm nguồn tín hiệu E, nội trở Z0 (phần thực R0), mắc nối
tiếp với ZL.Ta có thể coi ZL như một mạng một cửa có điện áp và dòng điện ngõ
vào lần lượt là V và I.
Ta có:
L
ZZ
E
I
0
(3.1)
L
L
ZZ
Z
EV
0
(3.2)
Công suất từ nguồn E đạt cực đại khi có sự phối hợp trở kháng giữa tải và
nguồn, nghĩa là:
*
0
ZZL
(liên hiệp phức) (3.3)
Ở vùng tần số siêu cao, điện áp và dòng điện tại bất kì điểm nào cũng đều
được coi là tổng của 1 sóng tới và 1 sóng phản xạ.
Dòng điện sóng tới được định nghĩa là dòng điện trong mạch khi có sự phối
hợp trở kháng (điều kiện (3.3)):
0
*
00 2R
E
ZZ
E
Ii
(3.4)
Điện áp sóng tới được tính khi có sự phối hợp trở kháng:
0
*
0
*
00
*
0
2R
EZ
ZZ
EZ
Vi
(3.5)
Vậy:
ii IZV *
0
(3.6)
Sóng phản xạ điện áp là:
(3.7)
Thay (3.2) và (3.5) vào (3.7), ta có:
i
L
L
L
L
L
L
L
L
r
V
ZZ
ZZ
Z
Z
ZZ
ZZ
Z
Z
ZZ
EZ
ZZ
ZZ
Z
Z
ZZ
EZ
ZZ
EZ
ZZ
EZ
V
0
*
0
*
0
0
0
*
0
*
0
0
*
00
*
0
0
*
00
*
0
*
00
*
0
*
00
*
0
0
1
(3.8)
Tương tự, sóng phản xạ dòng điện là:
)( ir III
(3.9)
Thay (3.1) và (3.4) vào (3.9), ta có:
Chương 3: Ma trận tán xạ
Trang 79
i
L
L
L
L
r
I
ZZ
ZZ
ZZ
ZZ
ZZ
E
ZZ
E
ZZ
E
I
0
*
0
0
*
00
*
00
0
*
00
1
(3.10)
Hệ số phản xạ điện áp:
L
L
i
r
v
ZZ
ZZ
Z
Z
V
V
S
0
*
0
*
0
0
(3.11)
Hệ số phản xạ dòng điện là:
i
r
iI
I
S
=
L
L
ZZ
ZZ
0
*
0
(3.12)
Trường hợp đặc biệt, nếu Z0 là điện trở thực (
00 RZ
) thì (3.11) và (3.12) sẽ
đồng nhất:
0
0
RZ
RZ
SSS
L
L
vi
(3.13)
Biểu thức (3.13) chính là hệ số phản xạ trên đường dây đã xét ở chương 1
Ta cũng có:
rr IZV 0
(3.14)
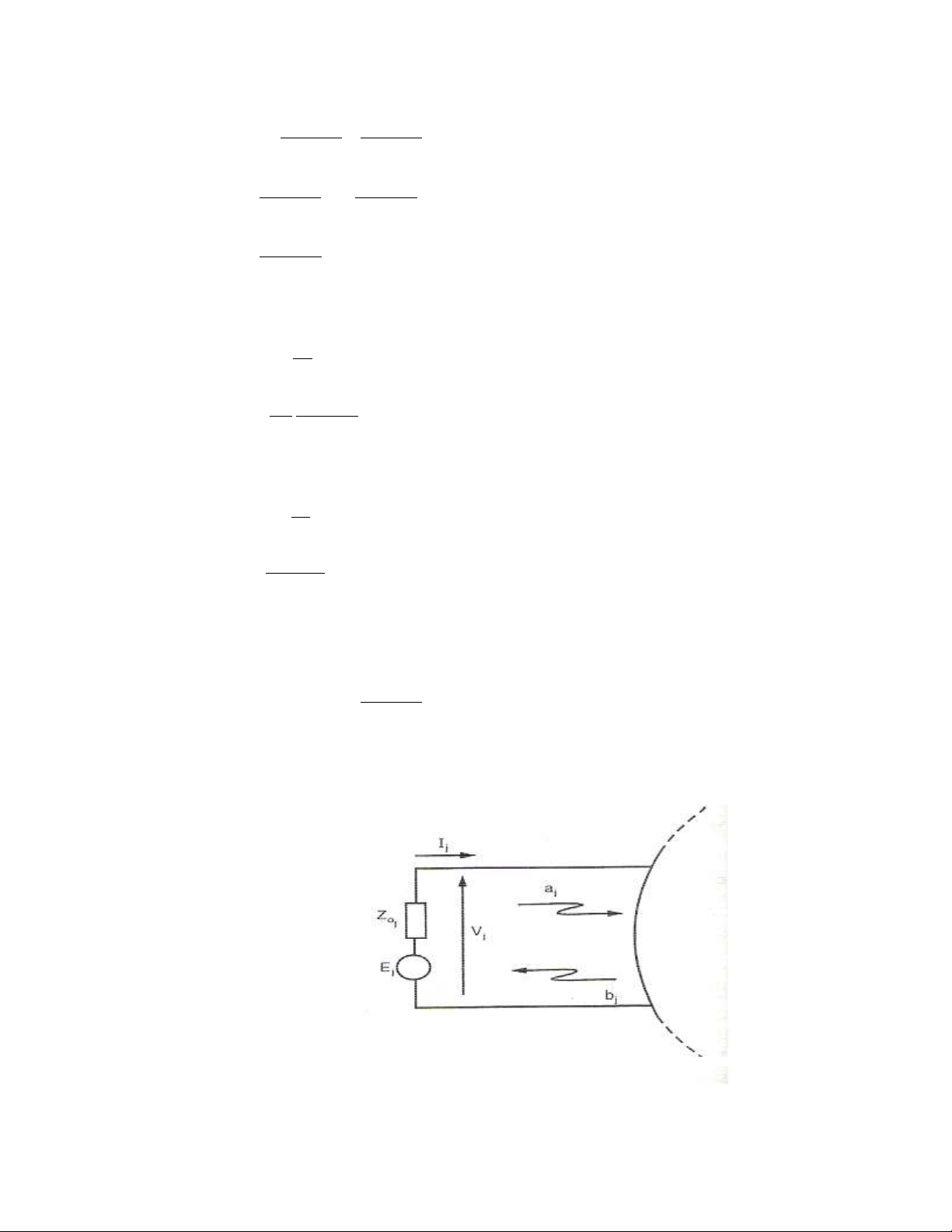
Cho mạng n cửa như hình 3.2. Xét cửa thứ j như hình
Chương 3: Ma trận tán xạ
Trang 80
Tại cửa j gồm nguồn Ej, nội trở R0j , Vij,Vrj, Iij, Irj là hiệu điện thế tới/về và
cường độ dòng điện tới/về.
Vj, Ij là hiệu điện thế và cường độ dòng điện tại ngõ vào bằng tổng của sóng
tới và sóng phản xạ:
rjijjVVV
(3.15)
rjijjIII
(3.16)
Ta định nghĩa ma trận trở kháng chuẩn [Z0] là ma trận đường chéo nxn gồm
các trở kháng chuẩn tại các cửa Z0j
Ta cũng định nghĩa các đại lượng điện áp và dòng điện sóng tới và sóng phản
xạ như là các vectơ cột n phần tử:
in
i
i
i
V
V
V
V
.
.
.
2
1
rn
r
r
r
V
V
V
V
.
.
.
2
1
in
i
i
i
I
I
I
I
.
.
.
2
1
rn
r
r
r
I
I
I
I
.
.
.
2
1
(3.18)
Vậy (3.15) và (3.16) được viết thành:
ri VVV
(3.19)
ri III
(3.20)
Ta cũng có quan hệ tương tự như (3.6) và (3.14):
ii IZV *
0
(3.21)
rr IZV 0
(3.22)
Tương tự như hệ số phản xạ điện áp và dòng điện được định nghĩa ở (3.11)
và (3.12) ta cũng có ma trận hệ số phản xạ điện áp và dòng điện:
ivr VSV
(3.23)
iir ISI
(3.24)
2. Ma trận tán xạ
S
Ma trận Tán Xạ
S
( Scattering Matrix) của một mạng n cửa được xây
dựng từ quan hệ của các đại lượng
a
và
b
liên quan đến công suất sóng tới
và sóng về( khác với sóng phản xạ). Với mạng n cửa , tại mỗi cửa thứ j đều có một
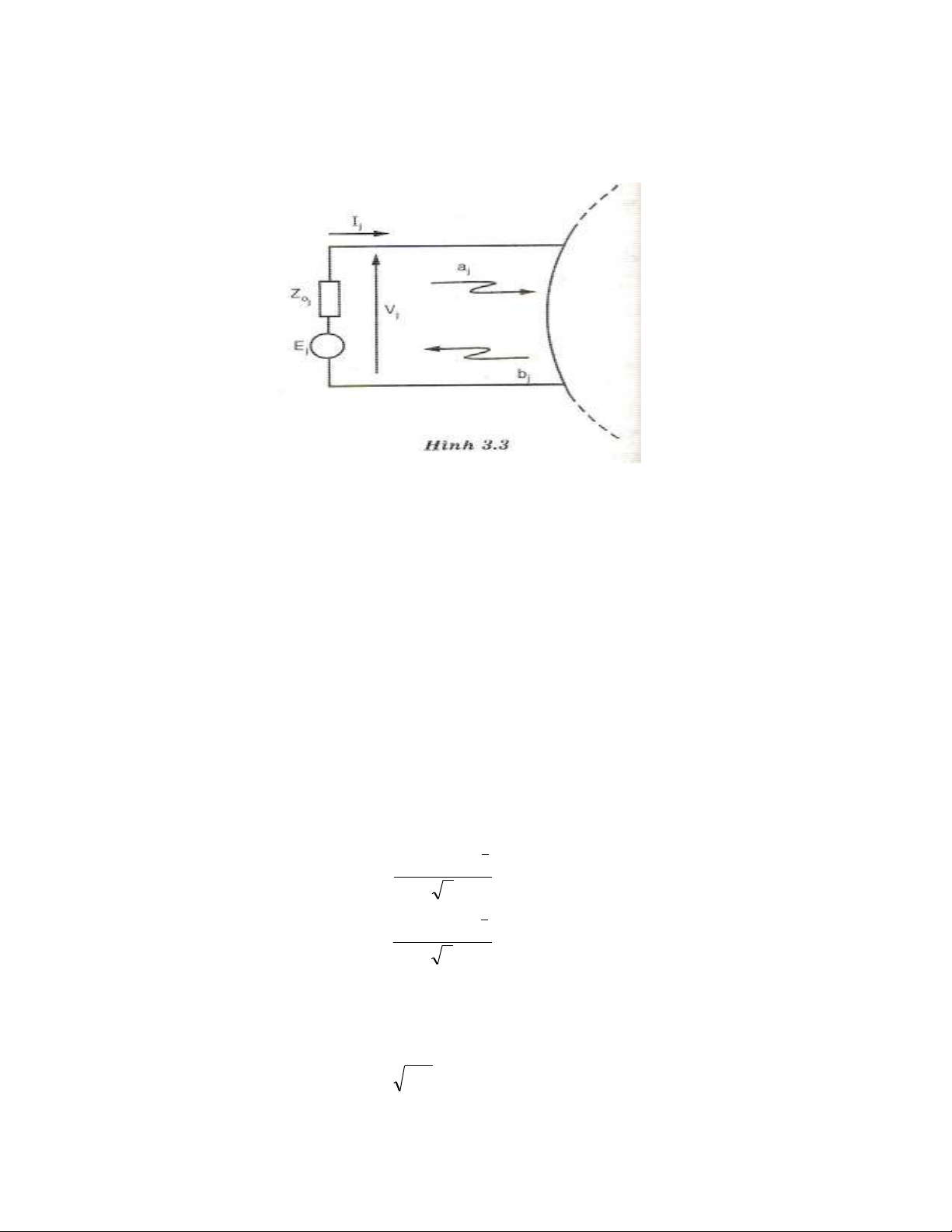
Chương 3: Ma trận tán xạ
Trang 81
thành phần sóng tới aj ( sóng đi vào cửa) và một thành phần sóng về bj ( sóng đi ra
khỏi cửa) như được vẽ ở hình 3.3
Sóng tới aj không những bao gồm công suất của nguồn tín hiệu E j tại cửa j
mà còn gồm công suất sóng từ nguồn khác phản xạ trên nội trở kháng Zoj để quay
vào cửa j.
Sóng về theo hướng đi ra khỏi cửa j không những bao gồm sóng phản xạ của
nguồn Ej tại ngõ vào cửa j mà còn gồm công suất của các nguồn khác vào mạng
tại các cửa khác và đi ra khỏi cửa j. Do đó ta không gọi tên đây là sóng phản xạ
mà gọi là sóng về.
n
a
a
a
a
.
.
2
1
;
3
2
1
.
.
b
b
b
b
(3.25)
Sóng tới [a] và sóng về [b] được định nghĩa như sau:
i
I
ZZ
a2
2
1
*
00
(3.26)
r
I
ZZ
b2
2
1
*
00
(3.27)
Trong đó, các ma trận [Z0], [Ii] và [Ir] được định nghĩa lần lượt theo (3.17) và
(3.18), (3.21), (3.22)
Nếu gọi R0j là phần thực của trở kháng chuẩn Z0j thì (3.26) và (3.27) có thể viết
thành:
ijjj IRa .
0
(3.28)