2. MCH DÃY
2.1 OTOMAT HU HN.
2.2 KHÁI NIM MCH DÃY.
2.3 CÁC LOI FLIP-FLOP.
2.4 THIT K MCH DÃY.
2.5 PHÂN TÍCH MCH DÃY.
2.6 THIT K MCH DÃY NG B.
2.7 THIT K MCH DÃY KHÔNG NG B.
2.8 MT S MCH DÃY THƯNG GP.
2.1 OTOMAT HU HN
2.1.1 Khái nim otomat hu hn.
Các mch logic c chia thành hai loi chính
là các mch t hp và các mch dãy.
- Các mch t hp là các mch logic không có
các phn t nh, còn gi là các otomat không có
nh.
- Các mch dãy (hay tun t, k tip..) là s kt
hp ca các mch logic và các mch nh, còn
gi là otomat có nh, gi tt là otomat.
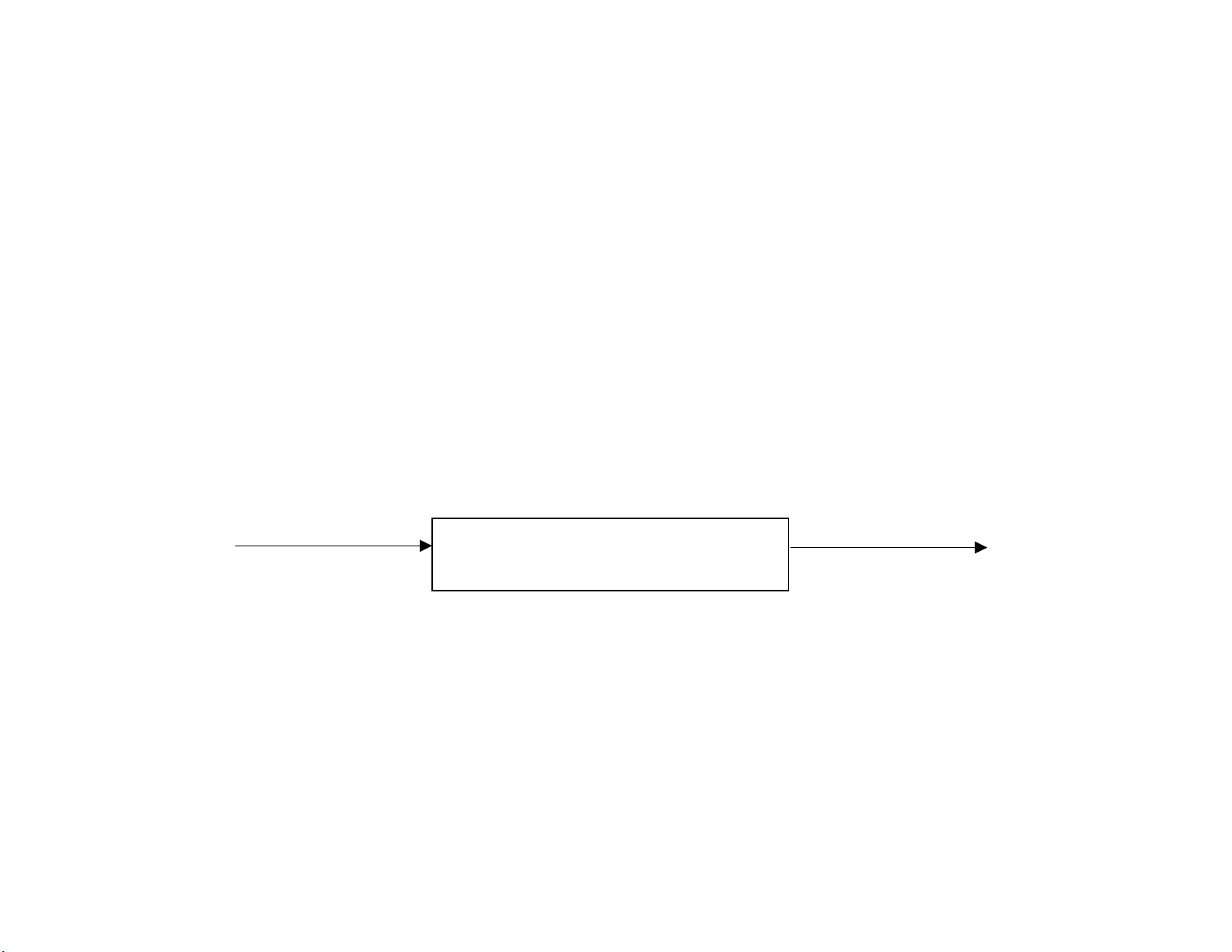
Mô hình tru tng ca otomat.
Mô hình Otomat là mt b bin i s có tp
các tín hiu vào Z={z
1
,z
2
,...z
i
,...z
F
}, tp các tín
hiu ra W={w
1
,w
2
,...w
j
,...w
G
}, tp các trng thái
trong A={a
1
,a
2
,...a
k
,...a
H
}, hai hàm c trưng là
hàm chuyn i trng thái và hàm u ra .
A={a
1
,...a
H
}
Z={z
1
,...z
G
}W={w
1
,...w
G
}
w(t)= (a(t),z(t))
a(t+1)=(a(t),z(t))
- Otomat hu hnlà otomat có các tp hp
A, Z, W h!u hn.
- Otomat xác nh hoàn toàn là otomat mà
"ng vi m#i cp (z
i
, a
k
) $ZxA các hàm c
trưng và là xác %nh.
-Otomat xác nh không hoàn toàn là
otomat ch&xác %nh vi mt scp (z
i
, a
k
) $
ZxA và không xác %nh vi mt scp (z
m
,
a
n
) $ZxA khác.
2.1.2 Các dng otomat và cách biu din.
Hai dng otomat:
- Otomat Moore là otomat mà tín hiu u ra
không ph' thuc tín hiu u vào, mà ưc xác
%nh b(ng trng thái trong ca nó ti cùng th)i
im.
- Otomat Mealy là otomat mà tín hiu ra ph'
thuc tín hiu vào và trng thái trong ti cùng
th)i im.