1. MCH LOGIC THP
1.1 C S LOGIC CA K THUT S.
1.2 PHÂN TÍCH MCH T HP.
1.3 THIT K MCH T HP.
1.4 MT S MCH T HP THNG GP.
1.5 CÁC VI MCH T HP VÀ LU Ý KHI
S DNG.
• Bin logic:
• T hp bin logic:
• Hàm logic:
• Bng chân lý:
1.1 CƠ S LOGIC CA KTS
1.1.1 BIN LOGIC VÀ HÀM LOGIC
{
}
1;0
=
∈
Bx
n
n
BxxxX ∈= ,...,,
21
(
)
{
}
1;0,...,,
21
=
∈
Bxxxf
n
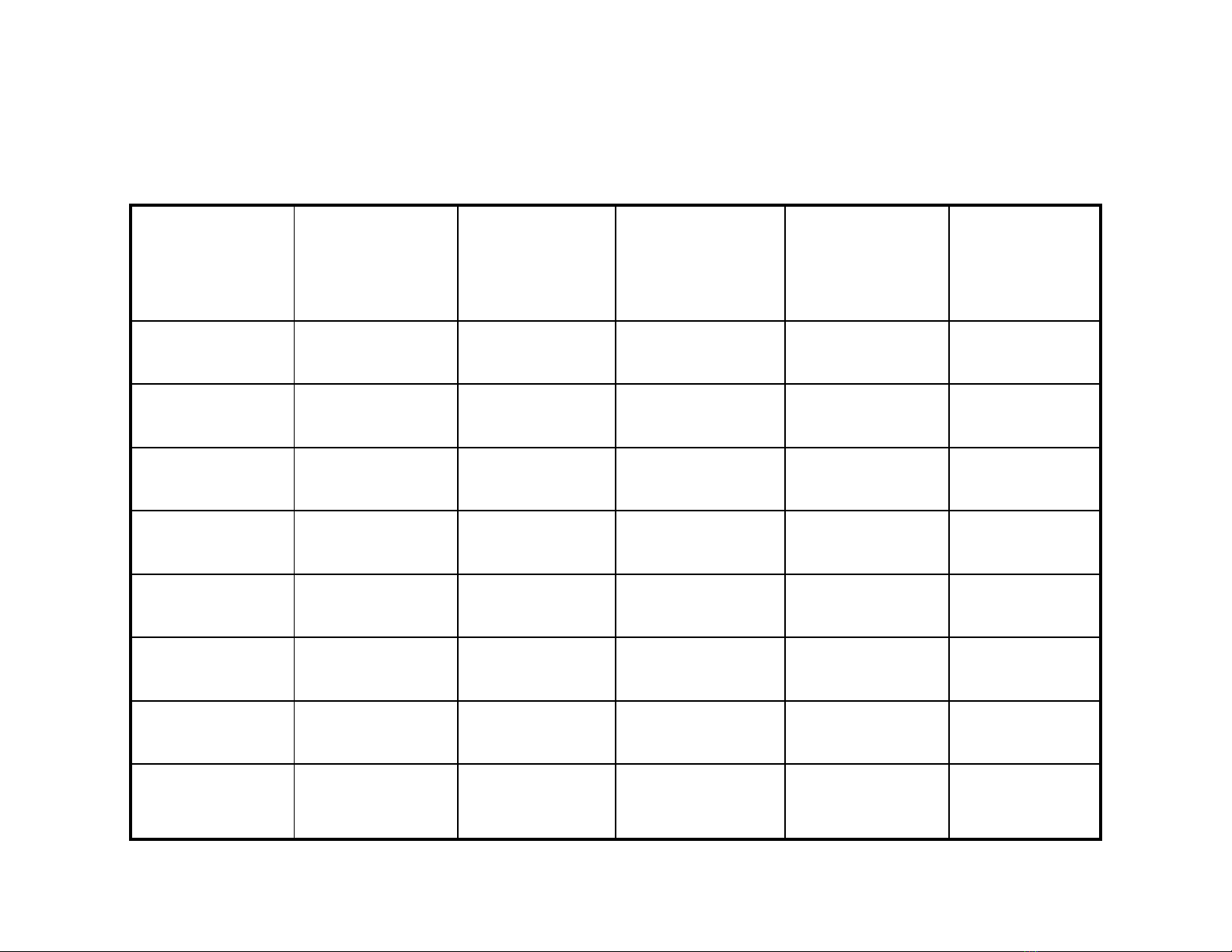
Ví d: Bng chân lý ca hàm logic
101117
100116
001015
000014
011103
100102
111001
010000
f
2
f
1
x
3
x
2
x
1
T hp
bin
Tp hp các giá tr ca t hp bin logic
• B
1
= B = {0;1} S phn t = 2
1
= 2
• B
2
= {00;01;10;11} S phn t = 2
2
= 4
• B
3
= {000;001;010;011;100;101;110;111}
S phn t = 2
3
= 8
• B
n
= {0..0;00..01;...;11..1}
S phn t = 2
n
Mi phn t là mt t hp các giá tr ca n
bin nh phân.
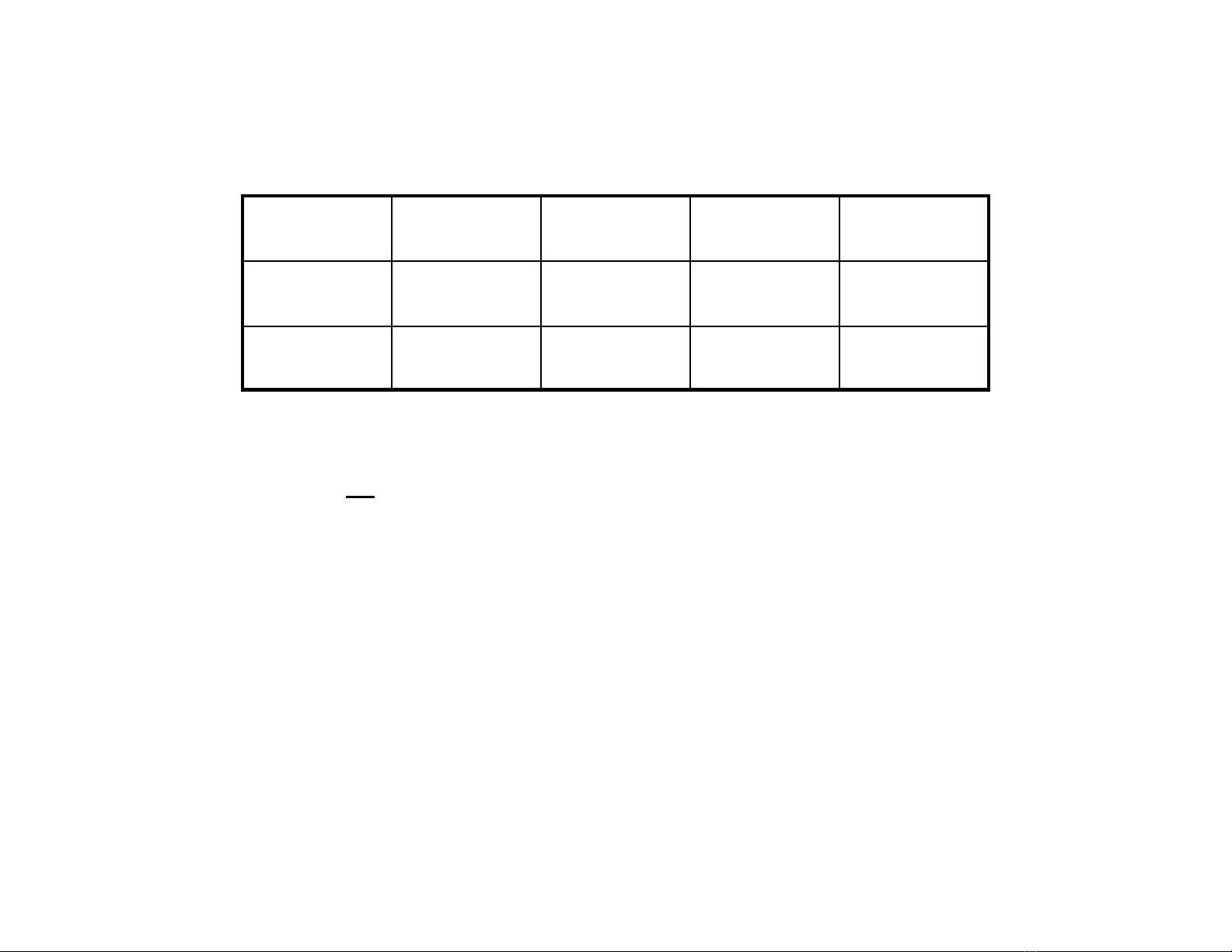
Các hàm logic mt bin f(x)
Hàm hng 0
Hàm ph nh
Hàm lp li
Hàm hng 1
S t hp bin:
S hàm logic:
11001
10100
f
4
f
3
f
2
f
1
x
xf =
2
0
1
f
xf
=
3
1
4
=
f
2
2
1
=
4
2
1
2
=