Taøi lieäu höôùng daãn töï hoïc moân Ñaïi soá vaø giaûi tích 11
----- Taøi lieäu löu haønh noäi boä -----
1
MOÄT SOÁ KÍ HIEÄU THOÂNG DUÏNG
Kí hieäu
Teân goïi
Dieãn giaûi
Pn
Soá caùc hoaùn vò cuûa n phaàn töû
Permutation
k
n
A
Soá caùc chænh hôïp chaäp k cuûa n phaàn töû
k
n
C
Soá caùc toå hôïp chaäp k cuûa n phaàn töû
Combinatory
P(A)
Xaùc suaát cuûa bieán coá A
Probability
n
ulim
Giôùi haïn cuûa daõy soá (un)
Limit
)(lim
0
xf
xx
Giôùi haïn cuûa haøm soá f(x) khi x daàn tôùi x0
Giôùi haïn cuûa haøm soá f(x) khi x daàn tôùi aâm voâ cöïc
Giôùi haïn cuûa haøm soá f(x) khi x daàn tôùi döông voâ cöïc
)(lim
0
xf
xx
Giôùi haïn beân phaûi cuûa haøm soá f(x) khi x daàn tôùi x0
)(lim
0
xf
xx
Giôùi haïn beân traùi cuûa haøm soá f(x) khi x daàn tôùi x0
y' hoaëc f'(x)
Ñaïo haøm cuûa haøm soá y = f(x)
y'' hoaëc f''(x)
Ñaïo haøm caáp hai cuûa haøm soá y = f(x)
y(n) hoaëc f(n)(x)
Ñaïo haøm caáp n cuûa haøm soá y = f(x)
dy hoaëc df(x)
Vi phaân cuûa haøm soá y = f(x)
Differenttial
n(A) hoaëc A
Soá phaàn töû höõu haïn cuûa taäp A
----- Voõ Thanh Huøng - THPT Traàn Quoác Toaûn - Ñoàng Thaùp -----
Taøi lieäu höôùng daãn töï hoïc moân Ñaïi soá vaø giaûi tích 11
----- Taøi lieäu löu haønh noäi boä -----
2
CHÖÔNG I. ÖÙNG DUÏNG ÑAÏO HAØM ÑEÅ KHAÛO SAÙT HAØM SOÁ
----- oOo -----
CHUAÅN BÒ KIEÁN THÖÙC:
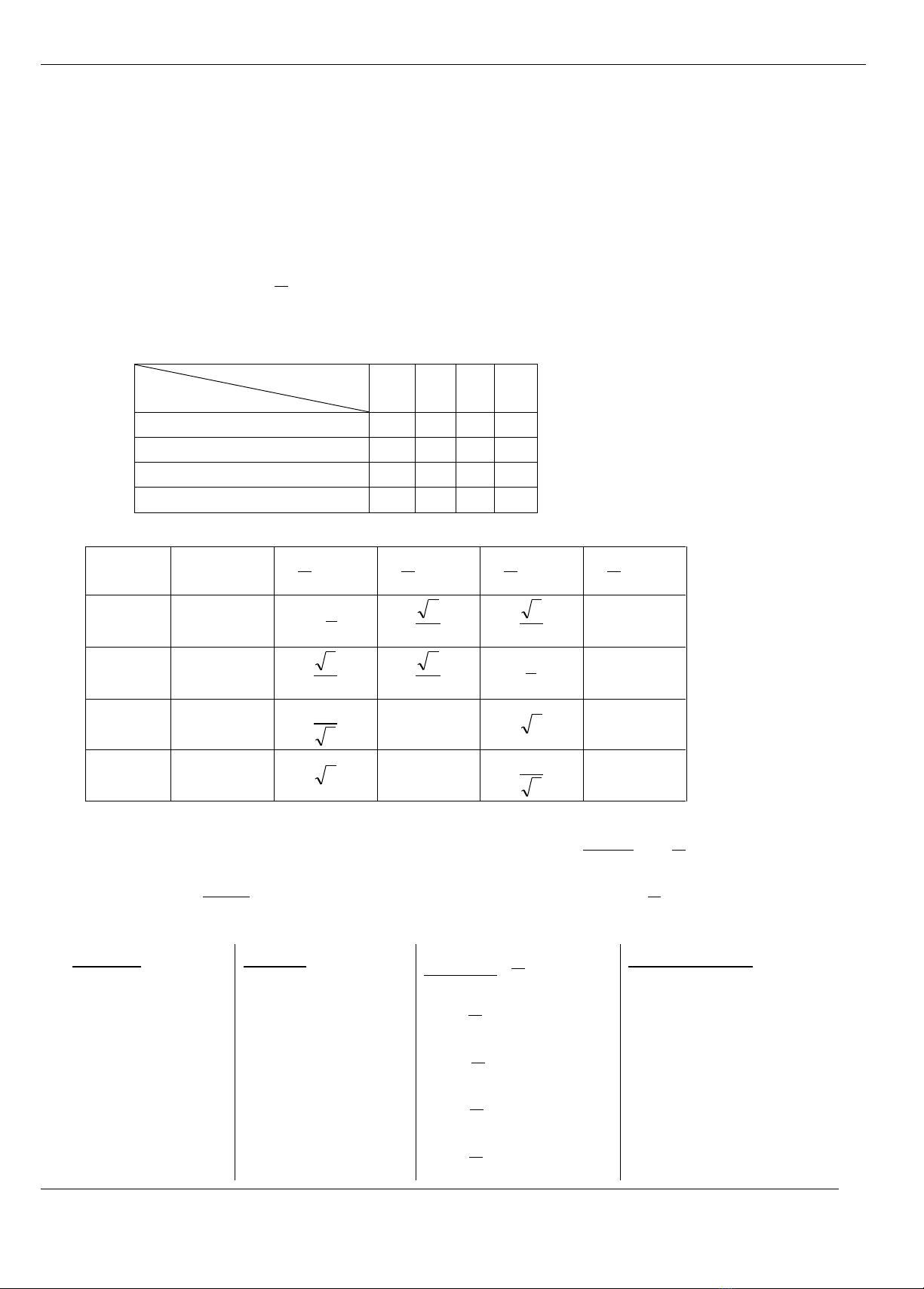
1. Caùc giaù trò löôïng giaùc cuûa cung (goùc) :
sin luoân xaùc ñònh  R vaø sin( + k2) = sin
cos luoân xaùc ñònh  R vaø cos( + k2) = cos
- 1 sin 1 (sin 1).
- 1 cos 1 (cos 1).
tan xaùc ñònh khi
k
2
vaø tan(k) = tan;
cot xaùc ñònh khi k vaø cot( + k) = cot.
Daáu cuûa caùc giaù trò löôïng giaùc cuûa goùc 
2. Baûng caùc giaù trò löôïng giaùc ñaëc bieät:
0 (00)
6
(300)
4
(450)
3
(600)
2
(900)
sin
0
2
1
2
2
2
3
1
cos
1
2
3
2
2
2
1
0
tan
0
3
1
1
3
kxñ
cot
kxñ
3
1
3
1
0
3. Coâng thöùc löôïng giaùc cô baûn:
sin2 + cos2 = 1
2
2
cos
1
tan1
(
k
2
, k Z).
2
2
sin
1
cot1
( k, k Z). tan.cot = 1 (
2
k
, k Z).
4. Giaù trò löôïng giaùc cuûa caùc cung coù lieân quan ñaëc bieät:
Cung ñoái:(-) vaø
sin(-) = -sin
cos(-) = cos
tan(-) = -tan
cot(-) = -cot
Cung buø:( - ) vaø
sin( - ) = sin
cos( - ) = -cos
tan( - ) = -tan
cot( - ) = -cot
Cung phuï:(
2
- ) vaø
sin(
2
- ) = cos
cos(
2
- ) = sin
tan(
2
- ) = cot
cot(
2
- ) = tan
Cung hôn keùm : ( + ) vaø
sin( + ) = -sin
cos( + ) = -cos
tan( + ) = tan
cot( + ) = cot
Phaàn tö
Giaù trò löôïng giaùc
I
II
III
IV
sin
+
+
-
-
cos
+
-
-
+
tan
+
-
+
-
cot
+
-
+
-
Taøi lieäu höôùng daãn töï hoïc moân Ñaïi soá vaø giaûi tích 11
----- Taøi lieäu löu haønh noäi boä -----
3
5. Caùc coâng thöùc löôïn giaùc thöôøng söû duïng:
Coâng thöùc coäng:
cos(a - b) = cosacosb + sinasinb
cos(a + b) = cosacosb - sinasinb
sin(a - b) = sinacosb - cosasinb
sin(a + b) = sinacosb + cosasinb
ba
ba
ba tantan1
tantan
)tan(
ba
ba
ba tantan1
tantan
)tan(
Coâng thöùc nhaân ñoâi:
sin2a = 2sinacosa
cos2a = cos2a - sin2a
= 2 cos2a - 1
= 1 - 2sin2a
atan1
2tana
2tan 2
a
Coâng thöùc haï baäc:
2
2cos1
cos2a
a
2
2cos1
sin2a
a
a
a
a2cos1
2cos1
tan2
Coâng thöùc bieán tích thaønh toång:
cosacosb =
2
1
[cos(a + b) + cos(a - b)]
sinasinb =-
2
1
[cos(a + b) - cos(a - b)]
sinacosb =
2
1
[sin(a + b) + sin(a - b)]
Coâng thöùc bieán ñoåi toång thaønh tích:
cosu + cosv = 2cos
2
vu
cos
2
vu
cosu - cosv = -2sin
2
vu
sin
2
vu
sinu + sinv = 2sin
2
vu
cos
2
vu
sinu - sinu = 2cos
2
vu
sin
2
vu
Coâng thöùc nhaân ba:
sin3a = 3sina - 4sin3a cos3a = 4cos3a - 3cosa
Coâng thöùc sina + cosa:
sina + cosa =
2
sin(a +
4
) sina - cosa =
2
sin(a -
4
)
sina + cosa =
2
cos(a -
4
) sina - cosa = -
2
cos(a +
4
)
Ghi chuù:
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................................
Taøi lieäu höôùng daãn töï hoïc moân Ñaïi soá vaø giaûi tích 11
----- Taøi lieäu löu haønh noäi boä -----
4
§1. HAØM SOÁ LÖÔÏNG GIAÙC
I- ÑÒNH NGHÓA:
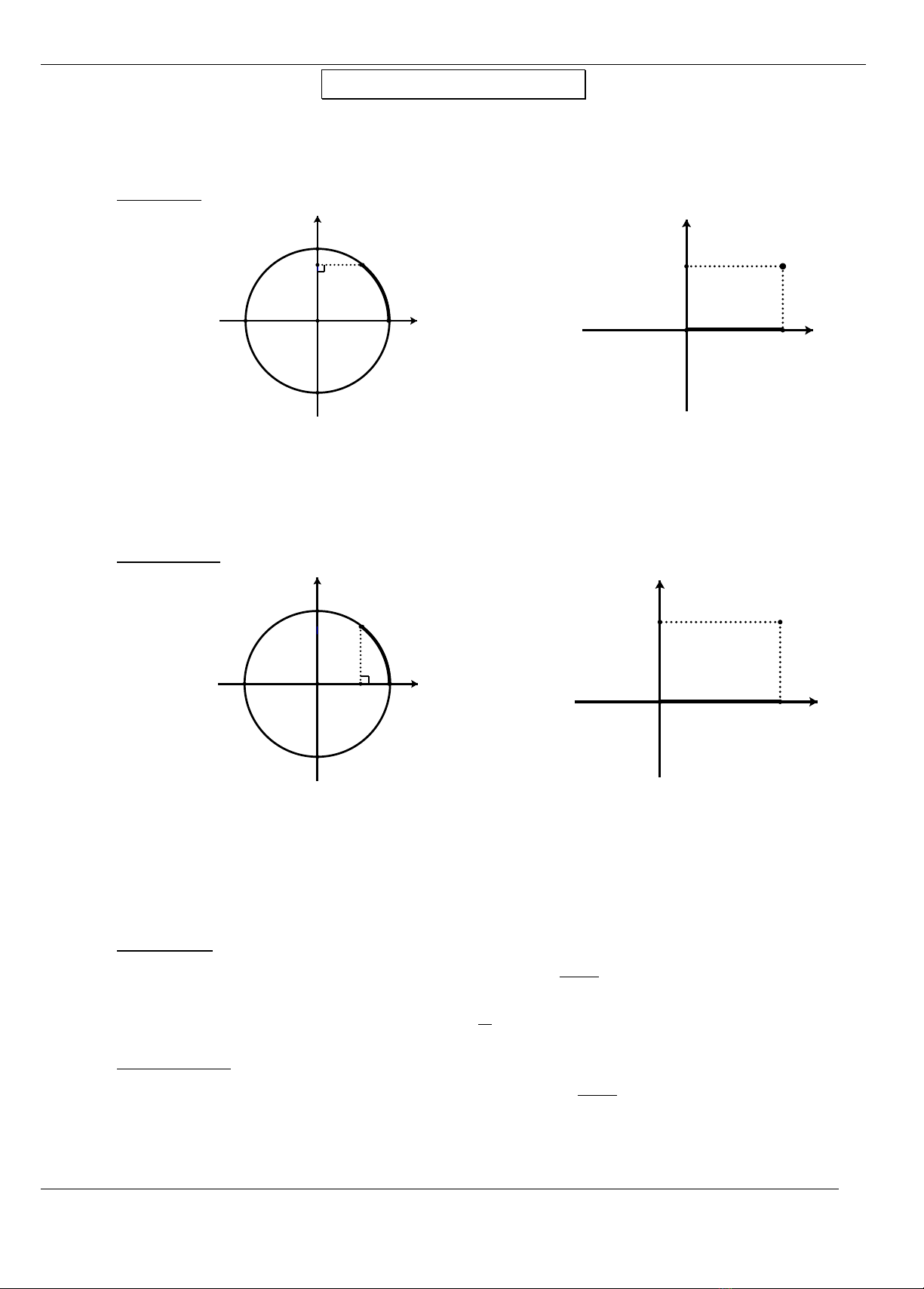
1. Haøm soá sin vaø haøm soá coâsin:
a) Haøm soá sin:
x
y
x
sinx
B'
A'
B
O
A
M
x
y
x
sinx
M'
O
Quy taéc ñaët töông öùng moãi soá thöïc x vôùi soá thöïc sinx
sin: R R
x
y = sinx
ñöôïc goïi laø haøm soá sin, kí hieäu laø y = sinx
Taäp xaùc ñònh cuûa haøm soá sin laø: D = R.
b) Haøm soá coâsin:
x
y
x
cosx
B'
A'
B
O
A
M
x
y
cosx
x
O
M''
Quy taéc ñaët töông öùng moãi soá thöïc x vôùi soá thöïc cosx
cos: R R
x
y = cosx
ñöôïc goïi laø haøm soá coâsin, kí hieäu laø y = cosx
Taäp xaùc ñònh cuûa haøm soá coâsin laø: D = R.
2. Haøm soá tang vaø haøm soá coâtang:
a) Haøm soá tang:
Haøm soá tang laø haøm soá ñöôïc xaùc ñònh bôûi coâng thöùc y =
x
x
cos
sin
(cosx ≠ 0), kí hieäu laø y = tanx.
Taäp xaùc ñònh cuûa haøm soá y = tanx laø: D = R\{
2
+ k, k Z}.
b) Haøm soá coâtang:
Haøm soá coâtang laø haøm soá ñöôïc xaùc ñònh bôûi coâng thöùc y =
x
x
sin
cos
(sinx ≠ 0), kí hieäu laø y = cotx.
Taäp xaùc ñònh cuûa haøm soá y = cotx laø: D = R\{k, k Z}.
Nhaéc laïi ñònh nghóa haøm soá chaün, haøm soá leû. Xeùt tính chaün, leû cuûa caùc haøm soá y = sin(x), y = cos(x), y = tan(x) vaø y = cot(x).
Taøi lieäu höôùng daãn töï hoïc moân Ñaïi soá vaø giaûi tích 11
----- Taøi lieäu löu haønh noäi boä -----
5
* Nhaän xeùt: Haøm soá y = sinx laø haøm soá leû, haøm soá y = cosx laø haøm soá chaün, töø ñoù suy ra caùc haøm soá
y = tanx vaø y = cotx ñeàu laø nhöõng haøm soá leû.
II- TÍNH TUAÀN HOAØN CUÛA HAØM SOÁ LÖÔÏNG GIAÙC:
Giaûi nghóa töø tuaàn hoaøn, laáy ví duï thöïc teá ñôøi soáng.
Tìm nhöõng soá T sao cho f(x + T) = f(x) vôùi moïi x thuoäc taäp xaùc ñònh cuûa caùc haøm soá: a) y = sinx; b) y = tanx.
Haøm soá y = sinx laø haøm soá tuaàn hoaøn vôùi chu kì 2.
Haøm soá y = cosx laø haøm soá tuaàn hoaøn vôùi chu kì 2.
Haøm soá y = tanx vaø y = cotx cuõng laø haøm soá tuaàn hoaøn, vôùi chu kì .
III- SÖÏ BIEÁN THIEÂN VAØ ÑOÀ THÒ CUÛA HAØM SOÁ LÖÔÏNG GIAÙC:
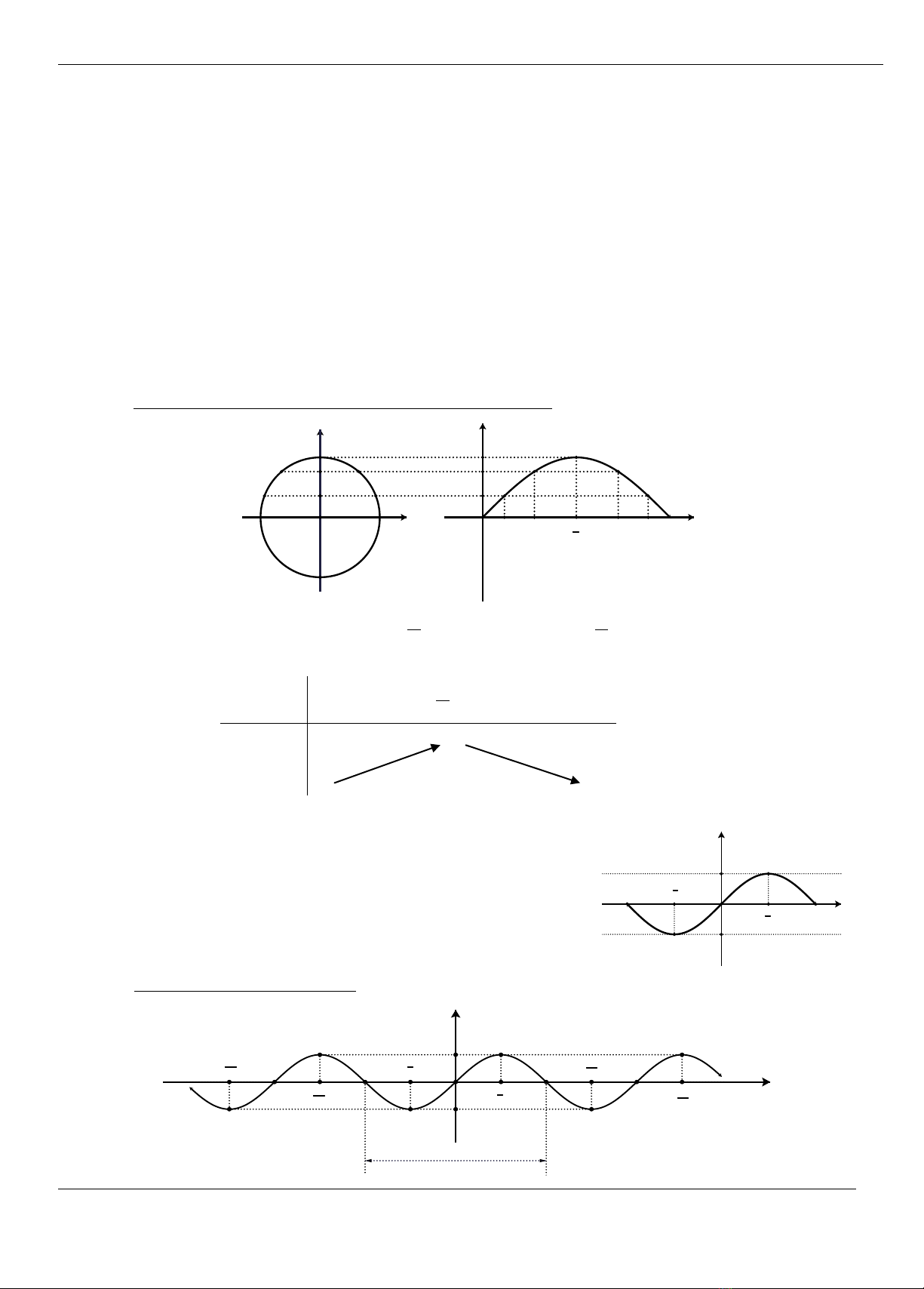
1. Haøm soá y = sinx:
Haøm soá y = sinx xaùc ñònh vôùi moïi x R vaø -1 sinx 1;
Laø haøm soá leû;
Laø haøm soá tuaàn hoaøn vôùi chu kì 2.
a) Söï bieán thieân vaø ñoà thò haøm soá y = sinx treân ñoaïn [0; ]:
sin
x
2
sin
x
1
1
x
1
x
2
x
3
x
4
sin
x
2
sin
x
1
y
x
x
y
2
x
4
x
3
x
2
x
1
A'
B'
A
B
O
O
Haøm soá y = sinx ñoàng bieán treân [0;
2
] vaø nghòch bieán treân [
2
; ].
Baûng bieán thieân:
x
0
2
y = sinx
1
0 0
* Chuù yù: Vì haøm soá y = sinx laø haøm soá leû neân laáy ñoái
xöùng ñoà thò haøm soá treân ñoaïn [0; ] qua goác toïa ñoä O,
ta ñöôïc ñoà thò haøm soá treân ñoaïn [-; 0].
2
-
2
-
-1
1
O
x
y
b) Ñoà thò haøm soá y = sinx treân R:
2
2
5
2
3
2
-
3
2
-
5
2
-2
2
-
2
-
-1
1
O
x
y