BÔ CUC BAI GIANG
1.Cac vi du dân đên bai toan Quy hoach tuyên
tinh:
1.1 Lâp kê hoach san xuât:
1.2 Phân bô vôn đâu t : ư
2. Đinh nghia:
1. Cac vi du dân đên bai toan Quy hoach tuyên
tinh (QHTT):
1.1 Lâp kê hoach san xuât:
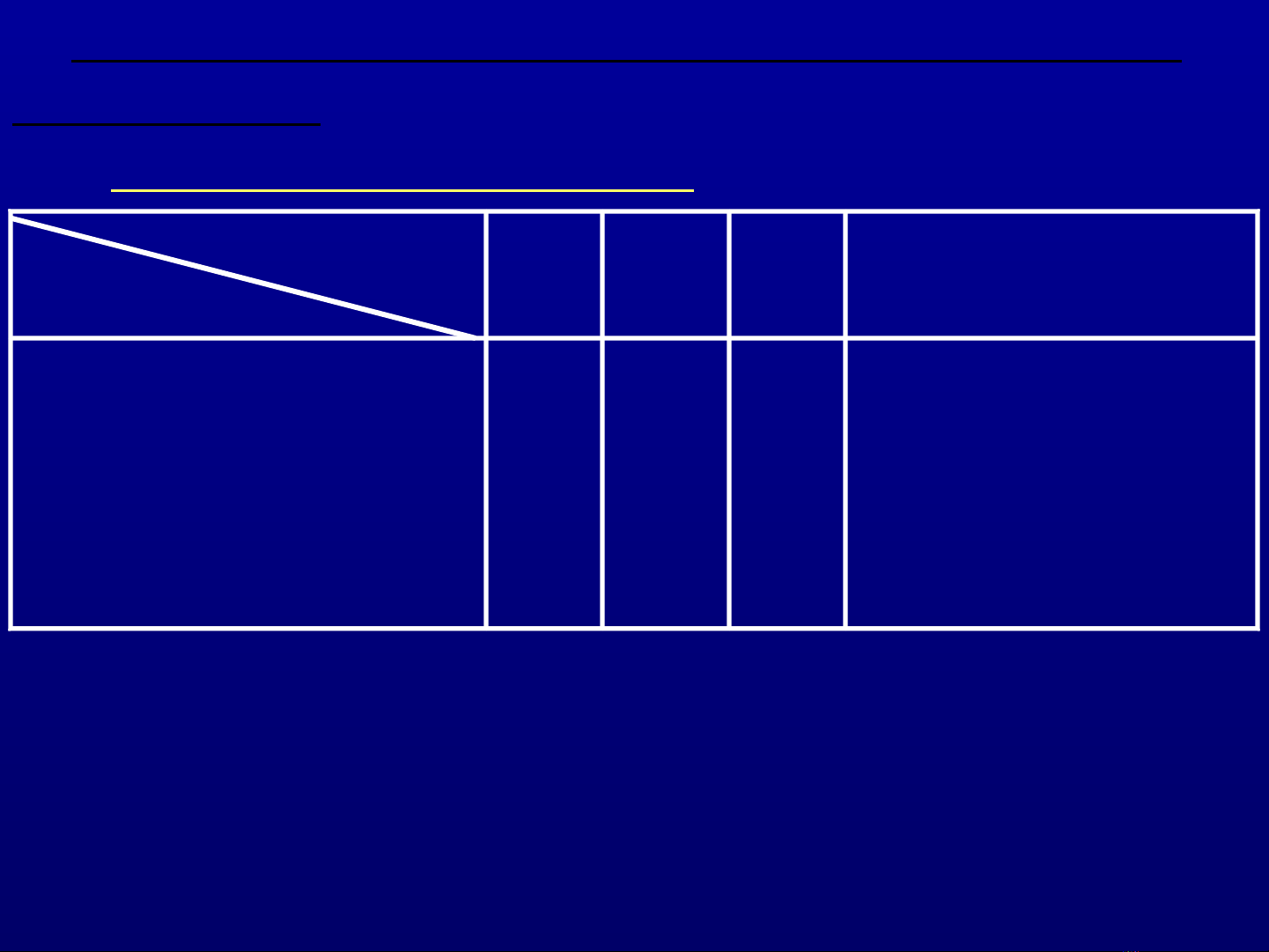
san phâm
Chi phiL1L2L3 Sô l ng nguyên ươ
liêu hiên co (kg)
Nguyên liêu 1 (N1)
Nguyên liêu 2 (N2)
Nguyên liêu 3 (N3)
Lao đông (phút)
4
2
3
10
5
4
6
7
3
3
4
6
15.000
12.000
10.000
500.000
Gia s răng san phâm san xuât ra đêu co thê tiêu thu đ c ư ươ
hêt v i l i nhuân khi ban môt đ n vi san phâm L ơ ơ ơ 1, L2, L3
t ng ng la 5000:10000:7000 (đông). Yêu câu lâp kê hoach ươ ư
san xuât tôi u. ư
Goi xj la sô san phâm cua L j (j = 1,2, 3) c n san xuât (xầ j
≥ 0, j = 1, 2, 3.)
1 2 3
4 5 3 15000x x x
+ +
1 2 3
2 4 3 12000x x x
+ +
N2:
1 2 3
3 6 4 10000x x x
+ +
N3:
Sô phut cân s dung: ư
1 2 3
10 7 6 500.000x x x+ +
Tông l i nhuân theo kê hoach san xuât la: ơ
1 2 3
5000 10000 7000x x x
+ +
Yêu c u t i u ầ ố ư
là:
5000 10000 7000 max
1 2 3
x x x+ +
Theo kê hoach san xuât phai tim l ng nguyên liêu tiêu ươ
hao la:
N1:
Mô hinh bai toan:
Tim x = (x1, x2, x3) sao cho:
( )
5000 10000 7000 max
1 2 3
4 5 3 15000
1 2 3
2 4 3 12000
1 2 3
3 6 4 10000
1 2 3
10 7 6 500000
1 2 3
0, 1,2,3
f x x x x
x x x
x x x
x x x
x x x
x j
j
= + +
+ +
+ +
+ +
+ +
=