Câu I (2.0 điểm) Cho hàm số
3 2 m
y x (m 1)x 3x m 1 (C )= − − − + +
1. Khảo sát sự biến thiên và vẽ đồ thị
(C)
của hàm số khi m 1.=
2. Tìm tất cả các giá trị của m để tiếp tuyến của đồ thị
m
(C )
tại điểm có hoành độ bằng 1
tạo với hai trục tọa độ một tam giác có diện tích bằng 2.
Câu II (2.0 điểm)
1. Giải phương trình:
2
2cos x 3cosx 2cos3x 4sin xsin2x+ − =
2. Giải hệ phương trình:
3 3
2 2
9y (3x 1) 125 (x;y )
45x y 75x 6y
− = −
∈
+ =
ℝ
Câu III (1.0 điểm) Tìm hệ số của số hạng chứa
4
x
trong khai triển sau:
n
5
3
3
1
nx x
+
biết
rằng n là số nguyên dương thỏa mãn:
1 2 2
n n
2C C n 20.
+ = −
Câu IV (2.0 điểm) Cho hình lập phương
ABCD.A'B'C'D'
có cạ
nh b
ằ
ng a. G
ọ
i M và N l
ầ
n
l
ượ
t là trung
đ
i
ể
m c
ủ
a các c
ạ
nh A'B' và B'C'.
1.
Tính th
ể
tích c
ủ
a kh
ố
i t
ứ
di
ệ
n AD'MN theo a.
2.
Tính kho
ả
ng cách gi
ữ
a hai
đườ
ng th
ẳ
ng AM và D'N.
Câu V (1.0 điểm)
Cho a, b, c là ba s
ố
d
ươ
ng th
ỏ
a mãn:
5a 5b 5c 3
+ + =
. Tìm giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a bi
ể
u th
ứ
c:
3 3 3
1 1 1
P2a 3b 2b 3c 2c 3a
= + +
+ + +
Câu VI (1.0 điểm)
Trong m
ặ
t ph
ẳ
ng Oxy, cho
đ
i
ể
m
A( 2;6)−
và hai
đườ
ng th
ẳ
ng
1 2
d , d
có
ph
ươ
ng trình l
ầ
n l
ượ
t là:
2x y 1 0
− − =
và
3x 4y 19 0
− − =
. Vi
ế
t ph
ươ
ng trình
đườ
ng tròn
(C) bi
ế
t (C) có tâm n
ằ
m trên
đườ
ng th
ẳ
ng
1
d
,
đ
i qua
đ
i
ể
m A và ti
ế
p xúc v
ớ
i
2
d .
Câu VII (1.0 điểm)
Gi
ả
i ph
ươ
ng trình:
( ) ( )
2 2 2
3x x 3x x 3x x 2
4 7 4 7 46.3 0
− − − −
− + + − =
-------------------------- Hết --------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
H
ọ
và tên thí sinh:........................................................ S
ố
báo danh:..................................
SỞ GD & ĐT BẮC NINH
TRƯỜNG THPT LÝ THÁI TỔ
ĐỀ THI THỬ ĐẠI HỌC LẦN I NĂM HỌC 2012-2013
Môn: TOÁN; Kh
ố
i B, D.
Thời gian: 180 phút, không kể thời gian phát đề.
Ngày thi 08/12/2012
C󰹄m ơn th󰹈y T󰹆n ( tan79@gmail.com) g󰺎i t󰹼i www.laisac.page.tl
Trang 1/3
Câu Đáp án Điểm
I
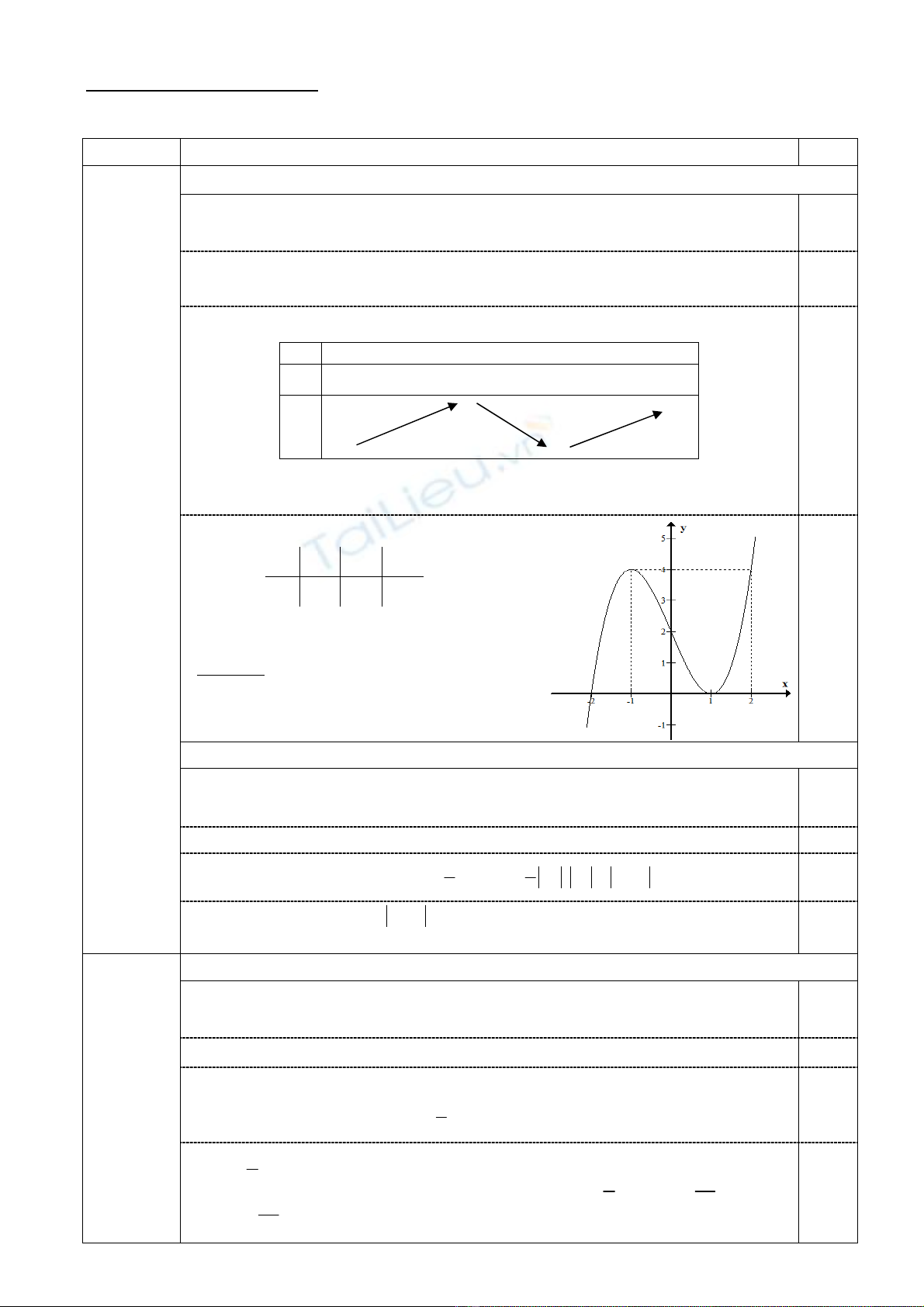
(2.0 điểm) 1. (1.0 điểm) Khảo sát vẽ đồ thị với 3
m 1 y x 3x 2=⇒=−+
▪ Tập xác định:
D=ℝ
.
▪ Sự biến thiên:x
lim y
→−∞
= −∞
, x
lim y
→+∞
= +∞
0.25
= − ⇒− =
= − = ⇔ − = ⇔ =⇒=
2 2
x 1 y( 1) 4
y' 3x 3, y' 0 3x 3 0 x 1 y(1) 0
0.25
▪ Bảng biến thiên:
Hàm số đồng biến trên các khoảng
( ; 1), (1; )−∞ − +∞
và nghịch biến trên
( 1;1)−
.
Hàm số đạt CĐ tại
C§
x 1, y 4= − =
và đạt CT tại
CT
x 1, y 0.= =
x
−∞
-1 1
+∞
'
y
+ 0 – 0 +
y
4
+∞
CĐ
CT
−∞
0
0.25
0.25
2. (1.0 điểm) Tìm m …
Với
=
⇒
=
⇒x 1 y 0 A(1;0)
. Ta có:
y' x (m )x= − − −
2
3 2 1 3
Phương trình tiếp tuyến của đồ thị
m
(C )
tại A là:
= − − − ∆y 2(m 1)(x 1) ( )
0.25
( )∆
cắt
Ox
tại
A(1;0)
và cắt
Oy
tại
− ≠B(0; 2m 2) (m 1)
0.25
Diện tích tam giác
OAB
là:
OAB A B
1 1
S OA.OB x . y m 1
2 2
∆
= = = − 0.25
Theo giả thiết:
∆
= ⇔ − = ⇔ = ∨ = −
OAB
S 2 m 1 2 m 3 m 1 (thoả mãn)
Vậy giá trị m thỏa mãn đề bài là: m 1= − và m 3=. 0.25
II
(2.0 điểm) 1. (1.0 điểm) Giải phương trình:
2
2 cos x 3cosx 2 cos(x 2x) 4 sin xsin 2x⇔ + − + =
⇔ + − − =
2
2 cos x 3cosx 2(cosx cos 2x sin x sin 2x) 4 sin x sin 2x
0.25
⇔ + − + =
2
2 cos x 3cosx 2(cosx cos 2x sin x sin 2x) 0
2
2cos x 3cosx 2cosx 0⇔ + − =
0.25
2
2cos x cosx 0⇔ + =
=
⇔= −
cosx 0
1
cosx 2
0.25
π
= + π
⇔π
= ± + π
x k
2
2
x k2
3
. Vậy nghiệm của p/trình đã cho là:
π π
= + π = ± + π
2
x k ; x k2 .
2 3
0.25
SỞ GD & ĐT BẮC NINH
TRƯỜNG THPT LÝ THÁI TỔ ĐÁP ÁN – THANG ĐIỂM
ĐỀ THI THỬ ĐẠI HỌC LẦN 1 NĂM 2013
Môn: TOÁN; Khối B, D
(Đáp án – thang điểm gồm 03 trang)
• Đồ thị:
x
1
2−
2
y 0 0
4
Ta có:
y'' 6x y'' 0 x 0=⇒= ⇔ =
⇒Đồ thị có 1 điểm uốn
I(0; 2)
Nhận xét: Đồ thị nhận điểm I(0; 2) làm
tâm đối xứng.
Trang 2/3
II
(2.0 điểm) 2. (1.0 điểm) Giải hệ phương trình…
Nhận thấy
y 0=
không là nghiệm của hệ
⇒≠y 0
Khi đó hệ tương đương
+ =
− = −
⇔
+ =
+ =
3
3
3
3
2
2
125
125 27x 9
27x 9 y
y
x 5
x x 15 3x 6
45 75 6 y y
yy
0.25
Đặt
u 3x
5
vy
=
⇒
=
Hệ trở thành:
+ = + − + =
⇔
+ = + =
3 3 3
u v 9 (u v) 3uv(u v) 9
uv(u v) 6 uv(u v) 6
+ =
+ =
⇔ ⇔
=
+ =
3u v 3
(u v) 27
uv 2
uv(u v) 6
= ∧ =
⇔= ∧ =
u 2 v 1
u 1 v 2
0.5
▪ Với
u x /
v y
=⇒=
=⇒=
2 2 3
1 5
▪ Với
u x /
v y /
=⇒=
=⇒=
1 1 3
2 5 2
Vậy nghiệm của hệ đã cho là:
(2 / 3;5), (1 / 3;5 / 2)
III
(1.0 điểm) Tìm hệ số của số hạng chứa 4
x
…
Ta có: 1 2 2
n n
2C C n 20 (1)+ = −
Điều kiện:
≥ ∈n 2; n ℤ
2 2
n 8
n(n 1)
(1) 2n n 20 n 3n 40 0 n 5 (lo¹i)2
=
−
⇒⇔ + = − ⇔ − − = ⇔ = −
0.25
Ta có:
()
8 8 k 40 14k
8 8
8 k
3 3 3
5 5 k 5 k 8 k 3
8 8
3 3 3
k 0 k 0
1 1 1
8x 2 x C 2 x C 2 x
x x x
−
−−
= =
+ = + = =
∑ ∑
0.25
Khai triển chứa
4
x
40 14k 4 k 2.
3
−
⇔ = ⇔ = 0.25
Vậy hệ số của
4
xlà:
2 6
8
C 2 1792.= 0.25
IV
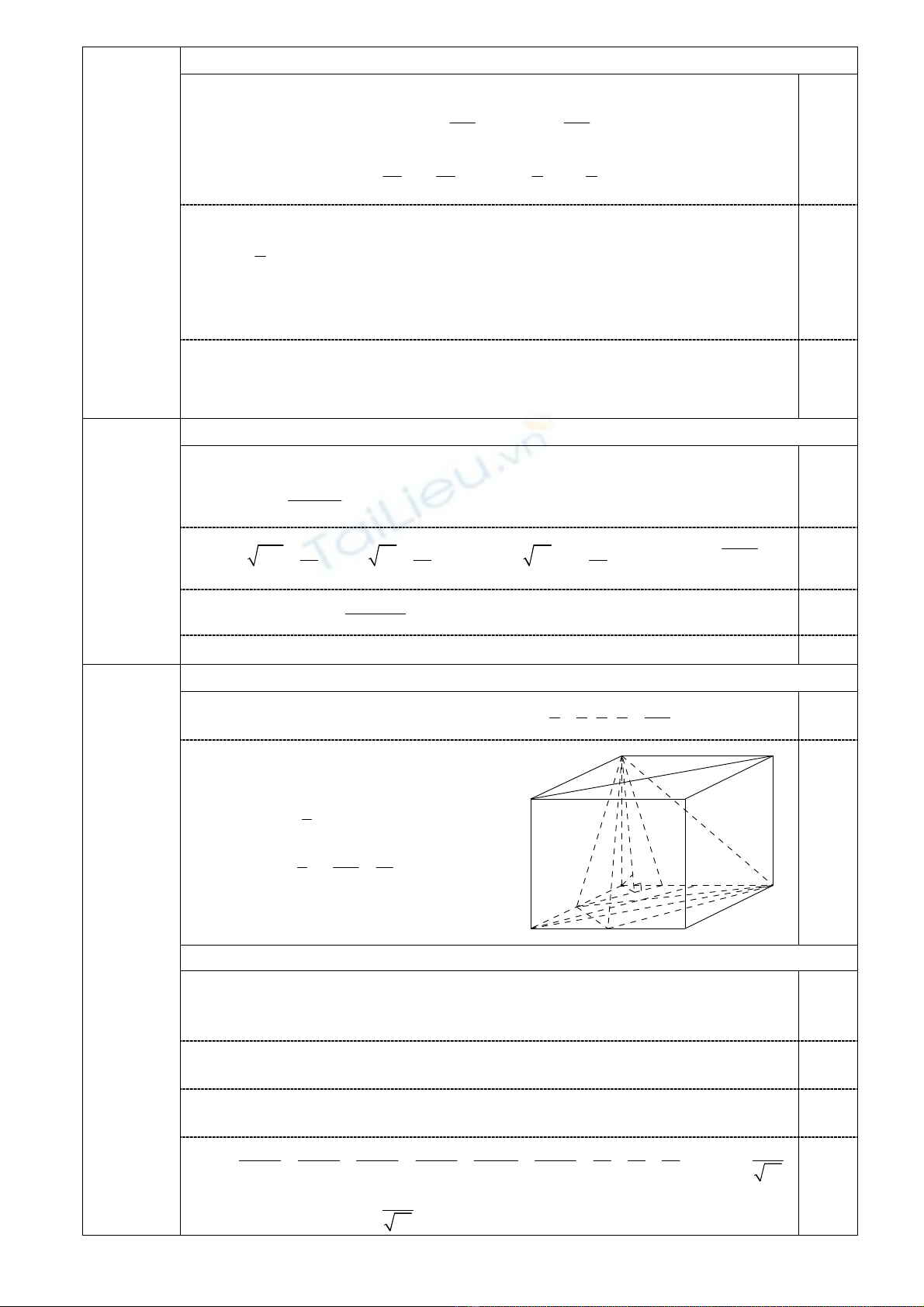
(2.0 điểm) 1. (1.0 điểm) Tính thể tích khối tứ diện AD'MN.
Ta có:
D ' C ' N
2
2
D 'MN A 'B 'C ' D' B 'MN
a 1 a a 3a
S S 2S S a a 2 2 2 2 8
∆
∆ ∆
= − − = − ⋅ − ⋅ ⋅ =
0.5
A
BC
D
A'
B' C'
D'
M
N
Q
H
K
P
0.5
2. (1.0 điểm) Tính khoảng cách giữa AM và
D'N
Trong
(A'B 'C ' D')
gọi P là trung điểm của
A'D ' B 'P⇒
//
D'N.
Trong
(A' B'C ' D')
kẻ MQ //
B' P (Q A'D ').∈
Do M là trung điểm của
A'B'
nên Q là
trung điểm của
A'P D 'Q 3A'Q.⇒=
0.25
Do
MQ
//
B' P ⇒
MQ //
D'N D'N⇒
//
(AMQ) d(AM,D'N) d(D'N,(AMQ))⇒=
d(D ',(AMQ)) 3d(A ',(AMQ))= =
(do
D'Q 3A'Q=
) 0.25
Trong
(A'MQ)
kẻ
A'K ⊥
MQ
MQ (AA'K)⇒⊥
. Trong
(AA'K)
kẻ
A'H AK.⊥
A'H (AMQ) d(A',(AMQ)) A'H.⇒⊥⇒=
0.25
Ta có:
2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 4 16 a
A'H
A' H A'A A'K A 'A A 'M A'Q a a a 21
= + = + + = + + ⇒=
Vậy
3a
d(AM,D ' N) 3A'H 21
= =
0.25
Theo giả thiết:
AA ' (A 'B 'C ' D')
⊥
AA'⇒
là đường cao của tứ diện
AD'MN.
Vậy
A.D 'MN D'MN
1
V AA' S
3
∆
= ⋅ ⋅
2 3
1 3a a
a
3 8 8
= ⋅ ⋅ =
Trang 3/3
V
(1.0 điểm) Tìm giá trị nhỏ nhất của biểu thức:
Ta có: Cauchy
33
2a 3b 1 1 2a 3b 2
2a 3b (2a 3b).1.1 3 3
+ + + + +
+ = + ≤ =
3
1 3
2a 3b 2
2a 3b
⇒≥+ +
+
Dấu “=” xảy ra khi và chỉ khi:
2a 3b 1.+ =
0.25
Tương tự ta có:
3
1 3
2b 3c 2
2b 3c ≥+ +
+
Dấu “=” xảy ra khi và chỉ khi:
2b 3c 1.+ =
3
1 3
2c 3a 2
2c 3a ≥+ +
+
Dấu “=” xảy ra khi và chỉ khi:
2c 3a 1.+ =
0.25
Với
x 0;y 0;z 0> > >
ta có:
Cauchy
3
3
1 1 1 3 1 1 1 9
(x y z) 3 xyz 9
x y z x y z x y z
xyz
+ + + + ≥ ⋅ = ⇒+ + ≥
+ +
Do đó:
1 1 1
P 3 2a 3b 2 2b 3c 2 2c 3a 2
≥ + +
+ + + + + +
27 27 3
2a 3b 2 2b 3c 2 2c 3a 2 5a 5b 5c 6
≥ = =
+ + + + + + + + + + +
0.25
Vậy min P 3= Dấu “=” xảy ra khi và chỉ khi
a b c 1 / 5.= = =
0.25
VI
(1.0 điểm) Viết phương trình đường tròn (C) …
Giả sử (C) có tâm I, bán kính R.
Do
∈
⇒
−
1
I d I(a;2a 1).
Mà
∈⇒= = + + −
2 2
A (C) R IA (a 2) (2a 7)
0.25
2
d
tiếp xúc với (C) 2
d(I,d ) R IA⇔ = =
− − −
⇔ = + + −
+ −
2 2
2 2
3a 4(2a 1) 19 (a 2) (2a 7)
3 ( 4)
0.25
2 2
a 3 (a 2) (2a 7)⇔ + = + + − ⇔ + + = − +
2 2
a 6a 9 5a 24a 53
a I( ; ) vaø R
a a a / I( / ; ) vaø R /
=
⇒
=
⇔ − + = ⇔
=
⇒
=
2
2 2 3 5
2 15 22 0 11 2 11 2 10 17 2
0.25
Vậy phương trình đường tròn (C) thỏa mãn đề bài là:
(x ) (y )− + − =
2 2
2 3 25
(x / ) (y ) /− + − =
2 2
11 2 10 289 4
0.25
VII.a
(1.0 điểm) Giải phương trình …
( ) ( )
2 2 2
3x x 3x x 3x x
9 4 7 9 4 7 46.3 0
− − −
⇔ − + + − =
2 2
3x x 3x x
4 7 4 7
9 9 46 0 (1)
3 3
− −
− +
⇔ + − =
0.25
Đặt:
2 2
3x x 3x x
4 7 4 7 1 4 7 4 7
t (t 0) do 1
3 3 t 3 3
− −
+ − − +
= > ⇒= ⋅ =
Khi đó, (1) trở thành:
2
23 8 7
t
99
9t 46 0 9t 46t 9 0 (tháa m·n)
t23 8 7
t9
+
=
+ − = ⇔ − + = ⇔ −
=
0.25
▪ Với
−
=
+ + +
=⇒= ⇔ − = ⇔
= −
2
3x x 2
2
x 1
23 8 7 4 7 4 7
t 3x x 2 x 2 / 3
9 3 3
0.25
▪ Với
2
3x x 2
2
23 8 7 4 7 4 7
t 3x x 2 0 VN (do 0)
9 3 3
− −
− + +
=⇒= ⇔ − + = ∆ <
Vậy tập nghiệm của phương trình đã cho là:
= = − ⋅x 1; x 2 / 3
0.25
------------------------Hết------------------------