
SỞGD&ĐTVĨNHPHÚC KỲKSCLTHIĐẠIHỌCNĂMHỌC20122013LẦN1
ĐỀTHIMÔN:TOÁN KHỐID
Thờigianlàmbài:180phút,khôngkểthờigiangiaođề
I.PHẦNCHUNGCHOTẤTCẢTHÍSINH (7,0điểm)
Câu I(2,0điểm). Chohàmsố 4 2
2 4y x mx = - + -cóđồthị
( )
m
C.( mlàthamsốthực)
1.Khảosátsựbiếnthiênvàvẽđồthịhàmsốkhim=2.
2.Tìmtấtcảcácgiátrịcủam để các điểmcựctrịcủađồthị
( )
m
Cnằmtrêncáctrụctọađộ.
Câu II(2,0điểm).
1.Giảiphươngtrình:
( )
sin tan 2 3 sin 3 tan 2 3 3x x x x + - =.
2.Giảibất phươngtrình: 1
3
3 <
-
+
+x
x
x.
Câu III(1,0điểm).Giảihệphươngtrình:
( ) ( )
2 2
2 3 8 1 0
8 3 13 0
x y y x
x x y y
ì + - + - =
ï
í + + + - =
ï
î
CâuIV(1,0điểm).ChohìnhlậpphươngABCD.A'B'C'D'cóđoạnthẳngnốihaitâmcủahaimặtbênkề
nhaucóđộdàibằnga.TínhtheoathểtíchkhốilậpphươngABCD.A'B'C'D'vàkhoảngcáchgiữahai
đườngthẳng AC' và B'D'.
Câu V(1,0điểm).Choba sốthựcdương , ,x y z thayđổi.Tìmgiátrịnhỏnhấtcủa biểuthức:
2 2 2
2 2 2
3 3 3
x y z
P x y z
yz zx xy
æ ö æ ö æ ö
= + + + + +
ç ÷ ç ÷ ç ÷
è ø è ø è ø.
II.PHẦNRIÊNG (3,0điểm):Thísinhchỉđượclàmmộttronghaiphần(phầnAhoặcB)
A.TheochươngtrìnhChuẩn
CâuVI.a(1,0điểm).TrongmặtphẳngvớihệtrụctọađộOxy,chođườngthẳng(d)cóphươngtrình
0x y - =vàđiểmM(2;1).Lậpphươngtrìnhđườngthẳng
( )
DcắttrụchoànhtạiA,cắtđườngthẳng (d)
tạiBsaochotamgiácAMBvuôngcântại M.
CâuVII.a(1,0điểm).TrongmặtphẳngvớihệtrụctọađộOxy,chođườngtròn(C1)cóphươngtrình
2 2 25x y + =,điểmM(1;2).Đườngtròn(C2)cóbánkínhbằng 2 10.Tìmtọađộtâmcủa(C2)saocho
(C2)cắt(C1)theomộtdâycungqua Mcóđộdàinhỏnhất.
CâuVIII.a(1,0điểm). Giảibấtphươngtrình: 3 2 2
2
12 1
3 81.
2
x x x
C A A
x - ³ -( *
x N Î )
B.TheochươngtrìnhNângcao
Câu VI.b (1,0 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm P(7;8) và hai đường
thẳng
( )
1 : 2 5 3 0,d x y + + =
( )
2 : 5 2 7 0d x y - - =cắtnhautạiA.Viếtphươngtrìnhđườngthẳng(d)đi qua
P vàtạovới 1 2
( ),( )d d mộttamgiáccântại Avàcódiệntíchbằng 29
2 .
CâuVII.b(1,0điểm).TrongmặtphẳngvớihệtrụctoạđộOxy,chođườngthẳng(d)cóphươngtrình
2 0x y + + = và đườngtròn(C1) có phương trình: 2 2 4 2 4 0x y x y + - + + =. Đường tròn (C2)có tâm
thuộc(d),(C2)tiếpxúcngoàivới(C1)vàcóbánkínhgấpđôibánkínhcủa(C1).Viếtphươngtrìnhcủa
đườngtròn (C2).
CâuVIII.b(1,0điểm).Chohàmsố
2 3
1
x mx
y x
+ +
= +.Tìmtấtcảcácgiátrịcủamđểhàmsốcócựcđại,
cựctiểuđồngthờihaiđiểmcựcđại,cựctiểucủađồthịnằmvềhaiphíacủađườngthẳng (d):2x+y1=0.
Hết
Cảm ơnthầyNguyễnDuyLiên(lientoancvp@vinhphuc.edu.vn)đãgửitới
www.laisac.page.tl
HƯỚNGDẪNCHẤMKSCLTHIĐẠIHỌCNĂM20122013LẦN1
MÔNTOÁNKHỐID
(Đápáncó06trang:từtrang1đếntrang6)
Câu Đápán Điểm
1.Khảosáthàmsố vớim=2. 1,00
Vớim=2,hàmsốtrởthành: 4 2
y x 4x 4 = - + -
*TXĐ: R0,25
*Sựbiếnthiêncủahàmsố:
Giớihạnvôcựcvàcácđườngtiệmcận: lim ; lim
x x
y y
®+¥ ®-¥
= -¥ = -¥0,25
Bảngbiếnthiên:
+Tacó: =
é
= - + = Û ê = ±
ë
3 0
' 4 8 ; ' 0 2
x
y x x y x
+Bảngbiếnthiên:
x ¥ - 20 2+ ¥
y’ +0 0+0
y
0
¥
0
4 ¥
Hàmsốđồngbiếntrênmỗikhoảng
( )
-¥; - 2và
( )
0; 2
Hàmsốnghịchbiếntrênkhoảng
( )
- 2;0và
( )
+¥ 2;
Điểmcựcđạicủađồthịlà
( )
- 2;0,
( )
2;0điểmcựctiểucủađồthịB(0;4)
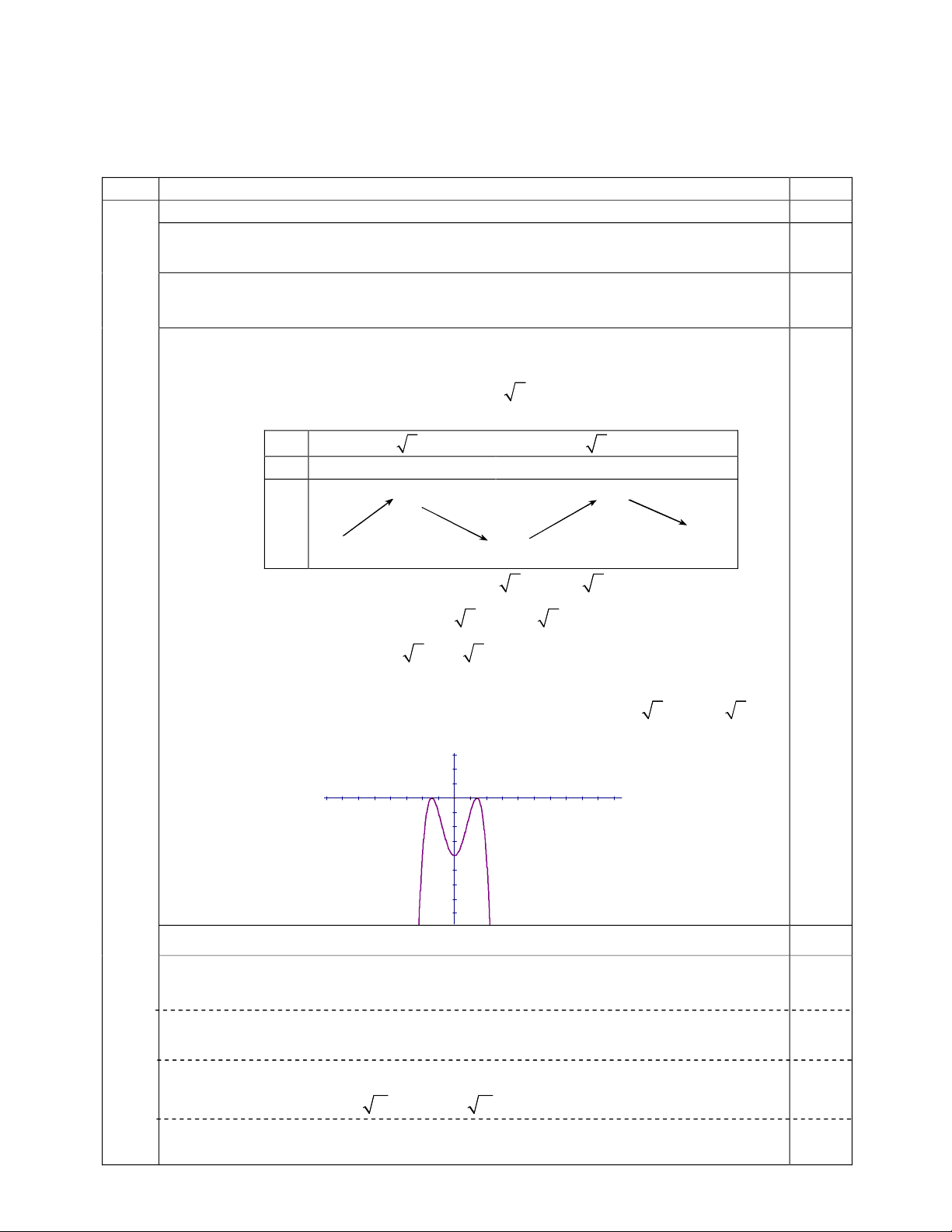
*Đồthị:
+Đồthịcắttrụctungtại
( )
0; 4 -vàcắttrụchoànhtạiđiểm
( )
2;0 -và
( )
2;0
+Nhậnxét:Đồthị(C)nhậntrụctunglàmtrụcđốixứng.
2
2
4
6
8
5 5 10
fx ( ) = x
4
+4×x
2
( ) 4
0,25
0,25
2. Tìmm đểtấtcảcáccựctrịcủahàmsố
( )
m
Cnằmtrêncáctrụctọađộ. 1,00
I
Tacó:
( )
3 2
2
0
' 4 4 4 ; ' 0x
y x mx x x m y x m
=
é
= - + = - + = Û ê =
ë
Nếu 0m £thì
( )
m
Cchỉcómộtđiểmcựctrịvàđólàđiểmcựcđạinằmtrêntrục
tung.
Nếu 0m >thì
( )
m
Ccó3điểmcựctrị.Mộtcựctiểunằmtrêntrụctungvàhai
điểmcựcđạicótọađộ 2
( ; 4)m m - -,2
( ; 4)m m -.
Đểhaiđiểmnày nằmtrêntrụchoànhthì
2 4 0 2m m - = Û = ±.Vì 0m >nênchọnm=2.
0,25
0,25
0,25

Vậy
{ }
( ;0] 2m Î -¥ Èlànhữnggiátrịcầntìmthỏamãnyêucầubàitoán. 0,25
1. Giảiphươngtrìnhlượnggiác 1,00
Đk. cos 2x 0 x m , m Z.
4 2
p p
¹ Û ¹ + Î
Tacó: sin tan 2 3(sin 3 tan 2 ) 3 3 + - =x x x x
(sin tan 2 3sin ) (3 tan 2 3 3) 0 Û + - + =x x x x
sin (tan 2 3) 3(tan 2 3) 0 (tan 2 3)(sin 3) 0x x x x x Û + - + = Û + - =
tan 2 3 2 ( ).
3 6 2
k
x x k x k Z
p p p
p
- -
Û = - Û = + Û = + Î(thỏamãn)
Vậy ptcómộthọnghiệm: , .
6 2
= - + Î
p p
x k k Z
0,25
0,25
0,25
0,25
2.Giảibấtphươngtrình 1,00
II
+Đk: x 0; x 3. ³ ¹
Bấtphươngtrình 3 x
x 1 3 x
+
Û < - -
2
2
2x 0
3 x
2x 4x
x x
3 x (3 x)
x 0
-
ì >
ï -
ï
- ï
Û < Û <
í
- -
ï
ï ³
ï
î
2
x (3; )
x 10x 9 0
Î +¥
ì
Û í - + <
î
x (3; ) x (3;9)
x (1;9)
Î +¥
ì
Û Û Î
í Î
î(Thỏamãnđiềukiện)
Vậytậpnghiệmcủabptlà:(3;9)
0,25
0,25
0,25
0,25
Giảihệphươngtrình... 1,00
III +Điềukiện: 2 2
3 0, 8 0x y y x + ³ + ³
Đặt
( )
2 2
3 , 8 , 0u x y v y x u v = + = + ³
+Tađược: 2 2 2 2 2 2
2 1 2 1 2 1
13 13 (2 1) 13
- = = - = -
ì ì ì
Û Û
í í í
+ = + = + - =
îîî
u v v u v u
u v u v u u
2
2 1
2 1 2
2
3
5 4 12 0 6( )
5
= -
ì
ï
= - =
ì ì
=
ïé
Û Û Û
í í í
ê =
- - = - î
î ï
ê =
ï
ë
î
v u
v u u
u
v
u u u loai
+Khiđó
2
2 2
2
2
2
2
4
33 2 3 4
4
8 9
8 3 8 9
3
ì -
=
ï
ì + = ì + =
ï ï ï
Û Û
í í í
æ ö
-
+ =
ï
+ = î ï ï
î + =
ç ÷
ï
è ø
î
x
y
x y x y
x
y x
y x x
0,25
0,25
0,25












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



