
Chng 1
XÁC SUT
Bài 1
TN SUT
MC TIÊU
1. Thc hin ưc ba phép toán tp hp (phép hp, phép giao, phép tr).
2. Tính ưc s lưng mu chnh hp lp, chnh hp không lp, t hp không lp và t hp lp.
3. Tính ưc tn sut ca hin tưng và nêu ưc ý ngha.
1. TP HP
1.1. Khái nim tp hp
Mi ngi thng nói tp hp bàn gh, tp hp s, tp hp thy thuc, tp hp bnh nhân v.v...
Tp hp là khái nim cha xác nh vì vy hiu và thc hin các phép toán vi tp hp th
ng thông
qua cách cho mt tp hp. Khi ó tp hp c xác nh.
Có hai cách cho tp hp: Hoc cho danh sách các phân t ca tp hp hoc cho các c tính, tính cht
xác nh mt phn t thuc tp hp.
Thng ký hiu các ch A, B, C, ... ch tp hp, các ch x, y, z,... ch phn t ca tp hp.
A
1
= {Danh sách (t viên) t 1},
A
2
= {Danh sách lp Y
1
},
A = {x thc : tho mãn tính cht Q(x)}.
Phn t x thuc A vit là x ∈ A. Phn t x không thuc B vit là x ∉ B hoc .
Tp hp trng là tp hp không cha mt phn t nào. Thng ký hiu tp hp trng là φ.
Ví d: A = {x thc : x
2
+ 1 = 0},
B = {Bác s chuyên m tim bnh vin huyn},
C = {Bnh nhân "ao" trên 50 tui}.
A, B, C là các tp hp trng.
Tp hp con
A là tp hp con ca B nu mi phn t x∈ A u là các phn t x∈B.
Ký hiu: A ⊆ B, c là A bao hàm trong B hoc B ⊇ A, c là B bao hàm A hoc B cha A.
T là tp hp con ca lp, lp là tp hp con ca khi.
Tp hp bnh nhân trong khoa bao hàm trong tp hp bnh nhân toàn vin.
x B
∈
Page
1
of
47
12/10/2012
file://C:\WINDOWS\Temp\ttwyprsdrx\Chapter1.htm
T
p h
p b
ng nhau.
Cho hai t
p h
p A và B. N
u m
i ph
n t
c
a A là nh
ng ph
n t
c
a B và ng
c l
i m
i ph
n t
c
a B
c
ng là nh
ng ph
n t
c
a A thì A = B.
ch
ng t
i
u này c
n ch
ng minh A ⊆ B và B ⊆ A.
1.2. Phép toán tp hp
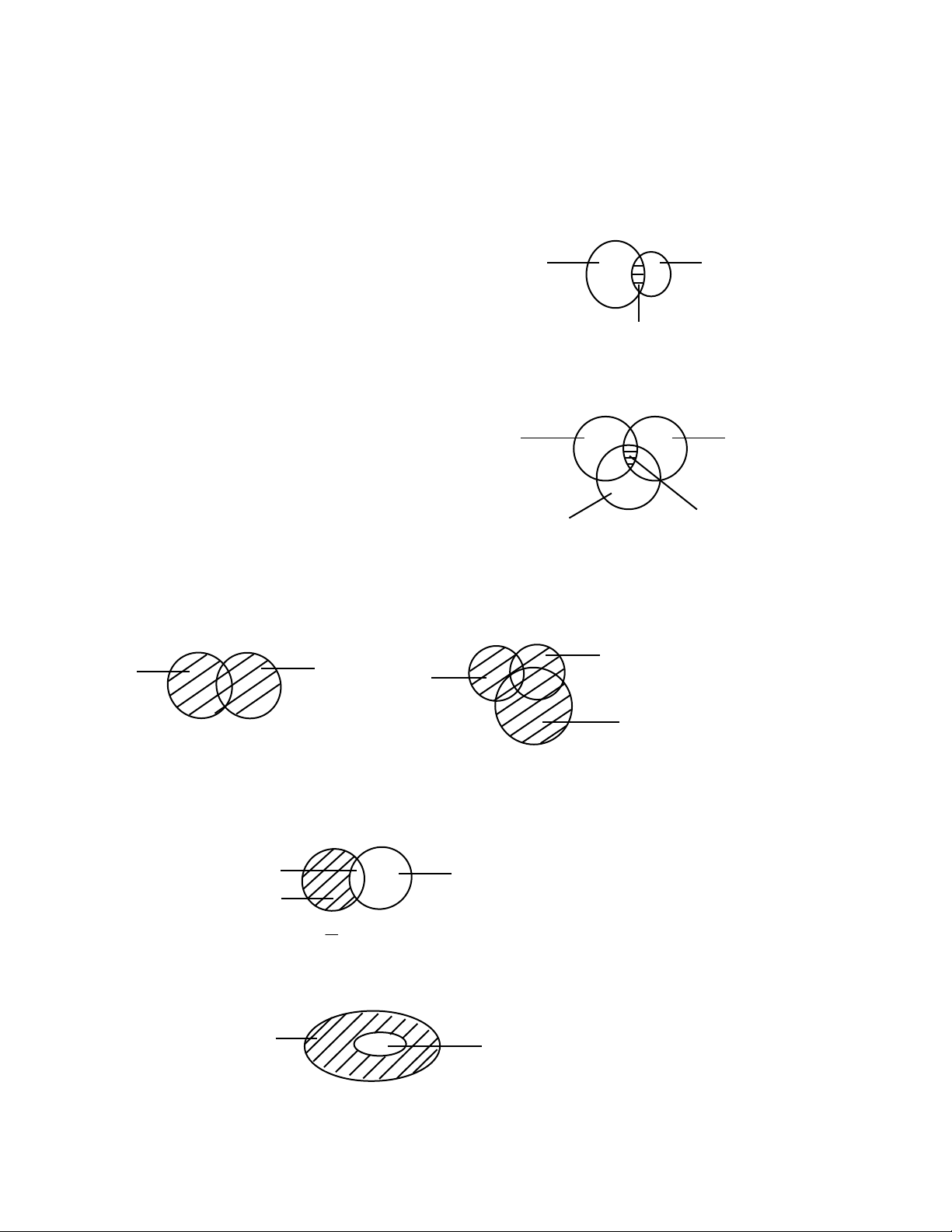
Phép giao
Cho A, B, C. Ký hi
u d
u ∩
c là giao.
Giao c
a hai t
p h
p A ∩ B = D
D là t
p h
p có các ph
n t
v
!
a thu
c A v
!
a thu
c B.
Giao c
a ba t
p h
p A ∩ B ∩ C = D
D là t
p h
p có các ph
n t
v
!
a thu
c A v
!
a thu
c B v
!
a thu
c C.
Chú ý:
Phép giao có th
m
r
ng cho nhi
u t
p h
p.
Th
ng vi
t A ∩ B ho
c vi
t t
"
t là AB.
Phép h
p
Cho A, B, C. Ký hi
u d
u ∪
c là h
p.
H
p c
a hai t
p h
p A ∪ B = E
E là t
p h
p có các ph
n t
ho
c thu
c A ho
c thu
c B ho
c thu
c A và B hay E là t
p h
p có các ph
n
t
thu
c ít nh
t m
t trong hai t
p h
p A, B.
H
p c
a ba t
p h
p A ∪ B ∪ C = E
E là t
p h
p có các ph
n t
thu
c ít nh
t m
t trong ba t
p h
p A, B, C.
Phép tr
!
Cho A, B. Ký hi
u A \ B
c là A tr
!
B hay hi
u c
a A và B.
A \ B = C. C là t
p h
p có các ph
n t
ch
thu
c A mà không thu
c B
Cho A ⊂ E . E \ A = C
E
A
=
C
E
A
c g
i là ph
n bù c
a A trong E hay
M
t s
tính ch
t
A
A
B
D
C
D
B
A
A
B
E
A
B
C
E
C
B
A
A
E
Page
2
of
47
12/10/2012
file://C:\WINDOWS\Temp\ttwyprsdrx\Chapter1.htm

A ∩ B = B ∩ A, A ∩ A = A, A ∩ φ = φ vì φ ⊂ A
A ∪ B = B ∪ A, A ∪ A = A, A ∪ φ = A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
1.3. Các khái nim khác
Tích
ecart (R. ecart)
Cho A = (x, y, z), B = (1, 2, 3).
Tích
ecart
c
a A và B vi
t là A × B.
A × B = { (x, 1), (x, 2), ..., (z, 3) }.
Tích
ecart
c
a A và B là m
t t
p h
p mà m
#
i ph
n t
là m
t c
p s
"
p th
t
, ph
n t
th
nh
t thu
c A,
ph
n t
th
hai thu
c B.
Nh
v
y, m
t
i
m trong m
t ph
$
ng 0xy là m
t ph
n t
c
a t
p h
p tích R × R. M(x, y) ∈ R × R = R
2
.
M
t
i
m trong không gian ba chi
u 0xyz là m
t ph
n t
thu
c t
p h
p tích
ecart
R × R × R
M(x, y, z) ∈ R × R × R = R
3
S
phân ho
ch m
t t
p h
p
Cho E. Chia E thành E
1
, E
2
, ..., E
n
sao cho tho
mãn các tính ch
t:
c g
i là phân ho
ch t
p h
p E.
Th
c ch
t s
phân ho
ch là vi
c chia sao cho m
#
i ph
n t
c
a E ch
thu
c v
duy nh
t m
t t
p h
p E
i
mà thôi.
Chia m
t l
p thành 4 t
ho
c chia b
nh nhân v
các khoa là phân ho
ch t
p h
p.
2. CÔNG THC M CÁC MU (GII TÍCH T HP)
Cho A = (x
1
, x
2
,.., x
n
)
Có bao nhiêu cách l
y k ph
n t
t
!
A ? S
cách l
y hay s
m
%
u ph
&
thu
c vào tính ch
t c
a m
%
u.
M
%
u l
p là m
%
u có ph
n t
xu
t hi
n trong m
%
u trên m
t l
n, m
%
u không l
p là m
%
u có m
#
i ph
n t
trong
m
%
u ch
xu
t hi
n m
t l
n.
Khi thay
i th
t
các ph
n t
trong m
%
u mà
c m
%
u m
i thì
ó là m
%
u có th
t
, n
u v
%
n là m
%
u c
thì
ó là m
%
u không th
t
. Hay nói cách khác, m
%
u có th
t
là m
%
u ph
&
thu
c th
t
các ph
n t
trong m
%
u,
ng
c l
i là m
%
u không th
t
.
2.1. Chnh hp lp
nh ngh
'
a
Cho A = (x
1
, x
2
,.., x
n
).
Chnh hp lp là mu k phn t có lp, có th t ly t n phn t ca A.
Công th
c
m
G
i s
cách l
y m
%
u hay s
l
ng m
%
u ch
nh h
p l
p là
Công th
c tính: = . Công th
c v
%
n
úng khi k > n.
M
t s
t
nhiên có 3 ch
s
là m
t m
%
u có l
p, có th
t
xây d
ng t
!
các ch
s
0, 1, ..., 9.
k
n
F
k
n
F
k
n
Page
3
of
47
12/10/2012
file://C:\WINDOWS\Temp\ttwyprsdrx\Chapter1.htm

S
m
%
u = 9. = 9 × 10
2
= 900
X
p tu
(
ý 5 b
nh nhân vào 3 khoa là m
t m
%
u có l
p, có th
t
xây d
ng t
!
3 khoa. S
m
%
u = = 3
5
=
243.
2.2. Chnh hp không lp
nh ngh
'
a
Cho A = (x
1
, x
2
,.., x
n
).
Chnh hp không lp là mu k phn t không lp, có th t ly t n phn t c
a
A.
Công th
c
m
G
i s
cách l
y m
%
u ch
nh h
p không l
p là
Công th
c tính :
Ký hi
u: n! = 1. 2. 3... n và quy
c 1! = 1, 0! = 1.
Công th
c
úng khi k
M
t s
t
nhiên có 3 ch
s
khác nhau là m
t m
%
u không l
p, có th
t
xây d
ng t
!
10 s
0, 1, …., 9. S
m
%
u = 9 × = 9 × 9 × 8 = 648.
X
p 3 b
nh nhân vào 5 khoa sao cho có nhi
u nh
t m
t ng
i trong khoa là m
%
u g
)
m 3 khoa không l
p,
có th
t
xây d
ng t
!
5 khoa. S
m
%
u = .
Hoán v
: cho A = (x
1
, x
2
,.., x
k
), m
#
i cách s
"
p x
p k ph
n t
là m
t hoán v
.
x
1
x
2
x
3
... x
k
và x
2
x
1
x
3
... x
k
là hai hoán v
khác nhau.
V
y hoán v
là m
%
u k ph
n t
không l
p, có th
t
l
y t
!
k ph
n t
.
G
i s
hoán v
là P
k
ta có công th
c tính: P
k
= k !
Nh
n xét : Ch
nh h
p l
p và ch
nh h
p không l
p là nh
ng m
%
u có th
t
.
2.3. T hp không lp
nh ngh
'
a
Cho A = (x
1
, x
2
,..., x
n
). T hp không lp là mu k phn t không lp, không th t ly t n phn t c
a
A.
Công th
c
m
G
i s
cách l
y m
%
u t
h
p không l
p là . Do t
h
p không l
p là m
%
u không th
t
c
a k phân t
l
y ra cho nên nhân s
t
h
p không l
p v
i k! s
*
c s
ch
nh h
p không l
p.
Công th
c:
Nh
n xét :
2
10
F
5
3
F
k
n
A
k
n
A n(n 1)...(n k 1).
= − − +
k
n
n!
A
(n k)!
=−
n.
≤
2
9
Α
3
5
5 4 3 60
Α = × × =
k
n
C
k
kn
n
An!
C , (k n)
k! (n k)! k!
= = ≤
−
k n k
n n
C C
−
=
Page
4
of
47
12/10/2012
file://C:\WINDOWS\Temp\ttwyprsdrx\Chapter1.htm

– Ch
n 5 ch
p hành chi
oàn trong s
8
ng c
và
c
là l
y m
%
u không l
p, không th
t
S
cách ch
n : .
– Gia
ình 3 con trong
ó có 2 gái là m
%
u không l
p, không th
t
, l
y 2 gái trong s
3 gái. S
lo
i gia
ình: .
L
p lu
n t
ơ
ng t
theo s
con trai c
ng
c k
t qu
trên.
2.4. T hp lp
nh ngh
'
a
Cho A = (x
1
, x
2
,..., x
n
). T hp lp là mu k phn t có lp, không th t ly t n phn t ca A.
Công th
c
m
N
u m
%
u l
p k ph
n t
thì ch
thêm k –1 ph
n t
l
p vào A d
%
n
n cách l
y m
%
u k ph
n t
không l
p,
không th
t
t
!
n + k – 1 ph
n t
.
Khi k > n công th
c c
ng
úng.
–
ơ
n th
c b
c 5 l
p t
!
a và b là m
%
u có l
p, không th
t
.
– Gia
ình 4 con là m
%
u có l
p, không th
t
l
p t
!
hai ph
n t
T (trai), G (gái).
Nh
n xét: M
%
u t
h
p không l
p và m
%
u t
h
p l
p là nh
ng m
%
u không th
t
.
Sau
ây xét m
t ví d
&
t
ng quát các lo
i m
%
u.
Ví d:
Cho A = (1, 2, 3, 4).
a) Có bao nhiêu s
t
nhiên có 3 ch
s
l
p t
!
4 s
ã cho ?
b) Có bao nhiêu s
t
nhiên có 3 ch
s
khác nhau l
p t
!
4 s
ã cho?
c) Có bao nhiêu nhóm có 3 ch
s
khác nhau l
p t
!
4 s
ã cho ?
d) Có bao nhiêu nhóm có 3 ch
s
l
p t
!
4 s
ã cho ?
Gii:
a) S
t
nhiên có 3 ch
s
là m
%
u có l
p, có th
t
l
p t
!
4 s
.
S
m
%
u b
ng :
b) S
t
nhiên có 3 ch
s
khác nhau là m
%
u không l
p, có th
t
l
p t
!
4 s
.
Công th
c tính:
S
ơ
n th
c là:
5
8
8!
C 56
(8 5)! 5!
= =
−
2
3
C 3
=
(
)
k
n k 1
n k 1 !
C
(n 1)! k!
+ −
+ −
=−
5
2 5 1
6!
C 6
1!5!
+ −
= =
4
2 4 1
5!
C 5
1! 4!
+ −
= =
3
4
F
3 3
4
F 4 64
= =
Page
5
of
47
12/10/2012
file://C:\WINDOWS\Temp\ttwyprsdrx\Chapter1.htm


























