Chương 2: Hàm số một biến số
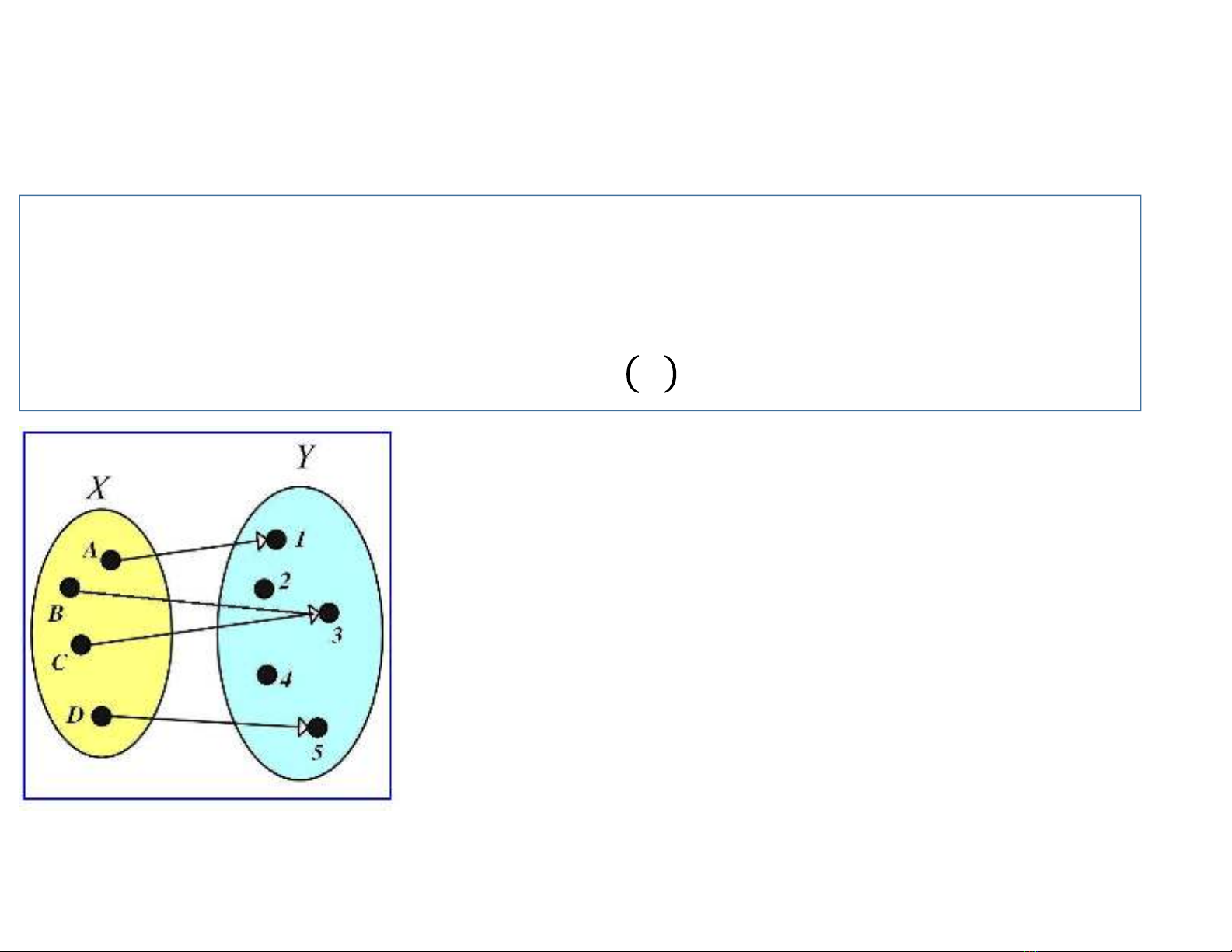
ĐỊNH NGHĨA HÀM HÀM SỐ
• Tập Xgọi là miền xác định.
• Tập Y=f(X) gọi là miền giá trị.
•xgọi là biến độc lập hay còn gọi là đối
số.
•y=f(x) gọi là biến phụ thuộc hay còn
được gọi là hàm số và được gọi là giá trị
của hàm ftại x.
Cho
,⊂ℝ,≠∅.
Một ánh xạ
từ
vào
được gọi
là hàm số của một biến số
:→
↦=
∀,∈;≠⇒ ≠()
.
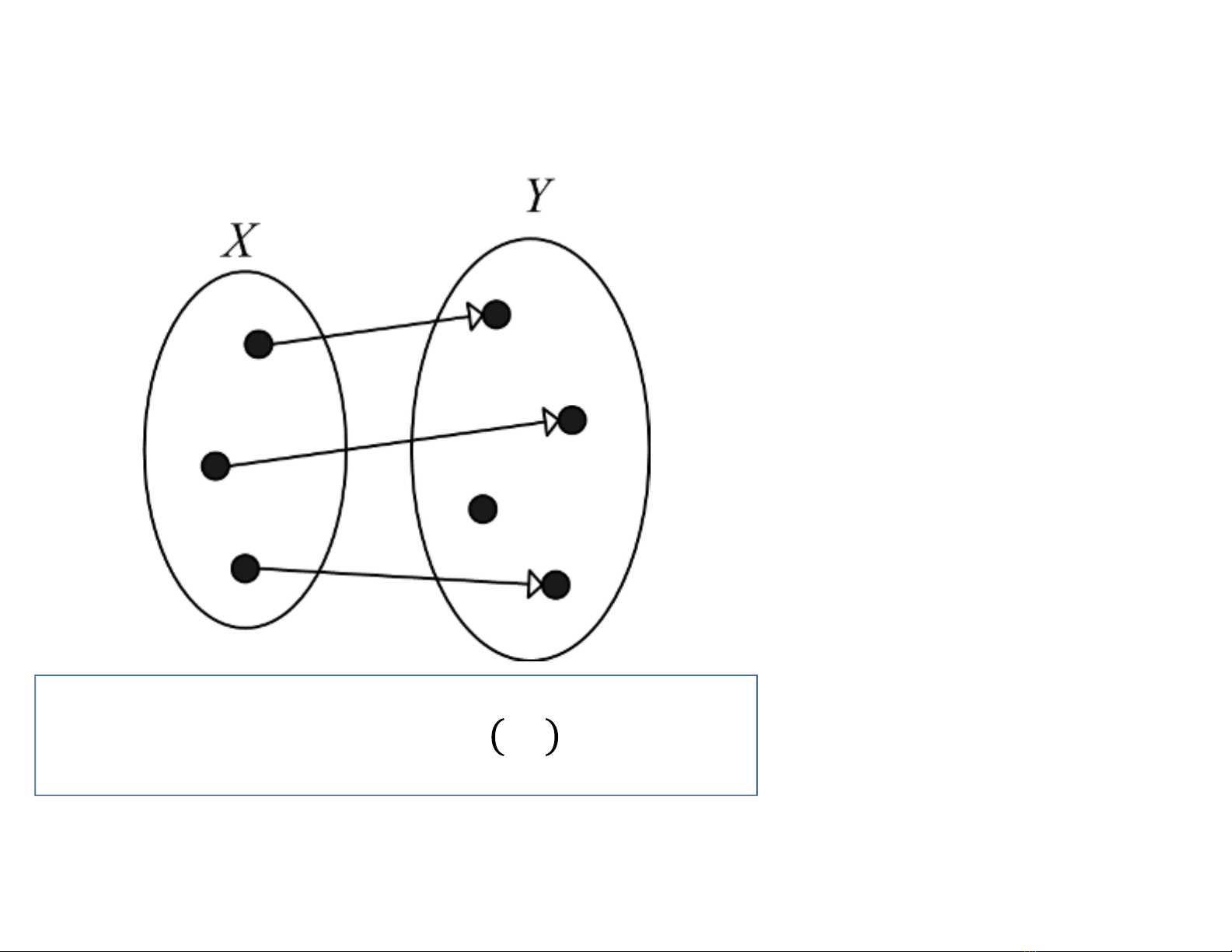
Đơn ánh.
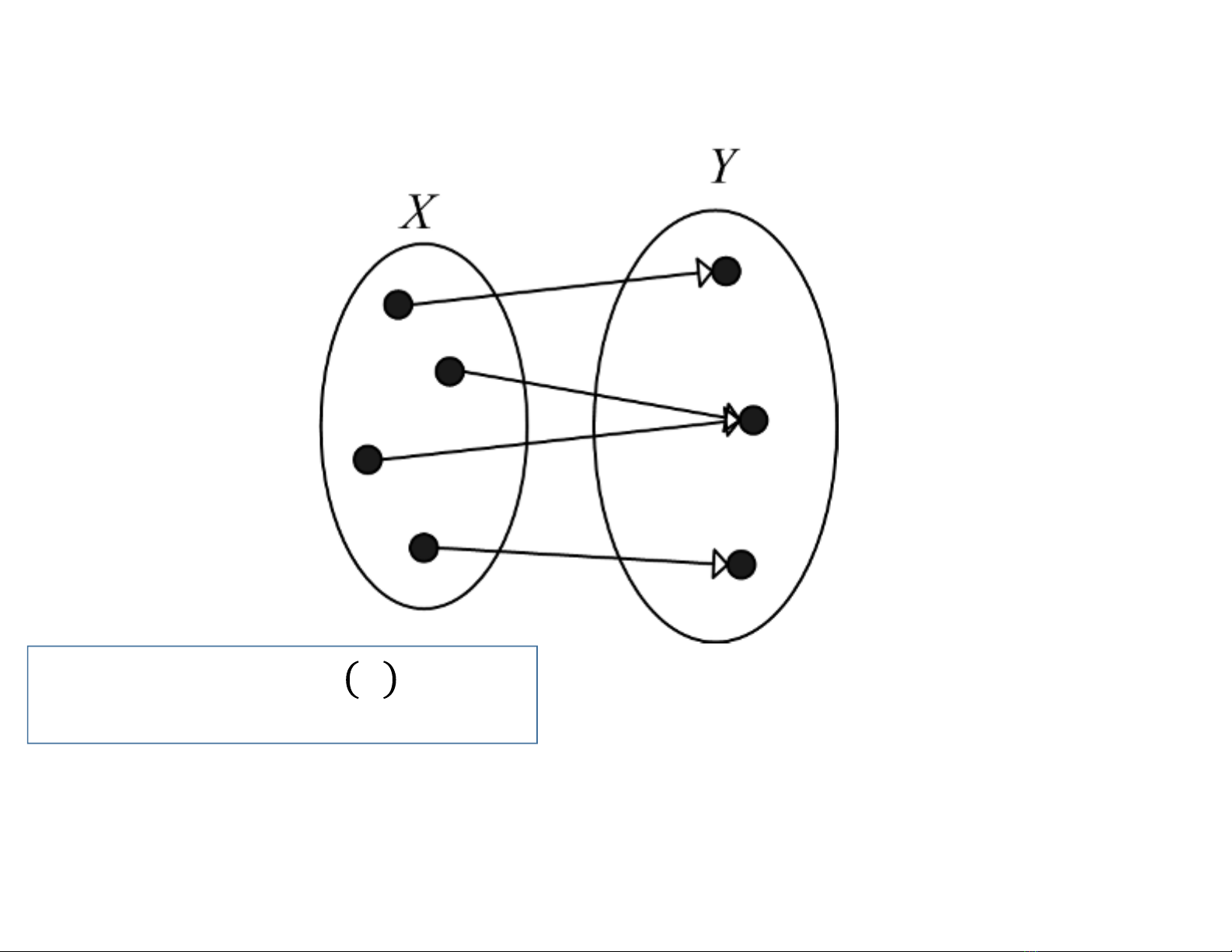
Toàn ánh.
∀∈,∃∈: =.
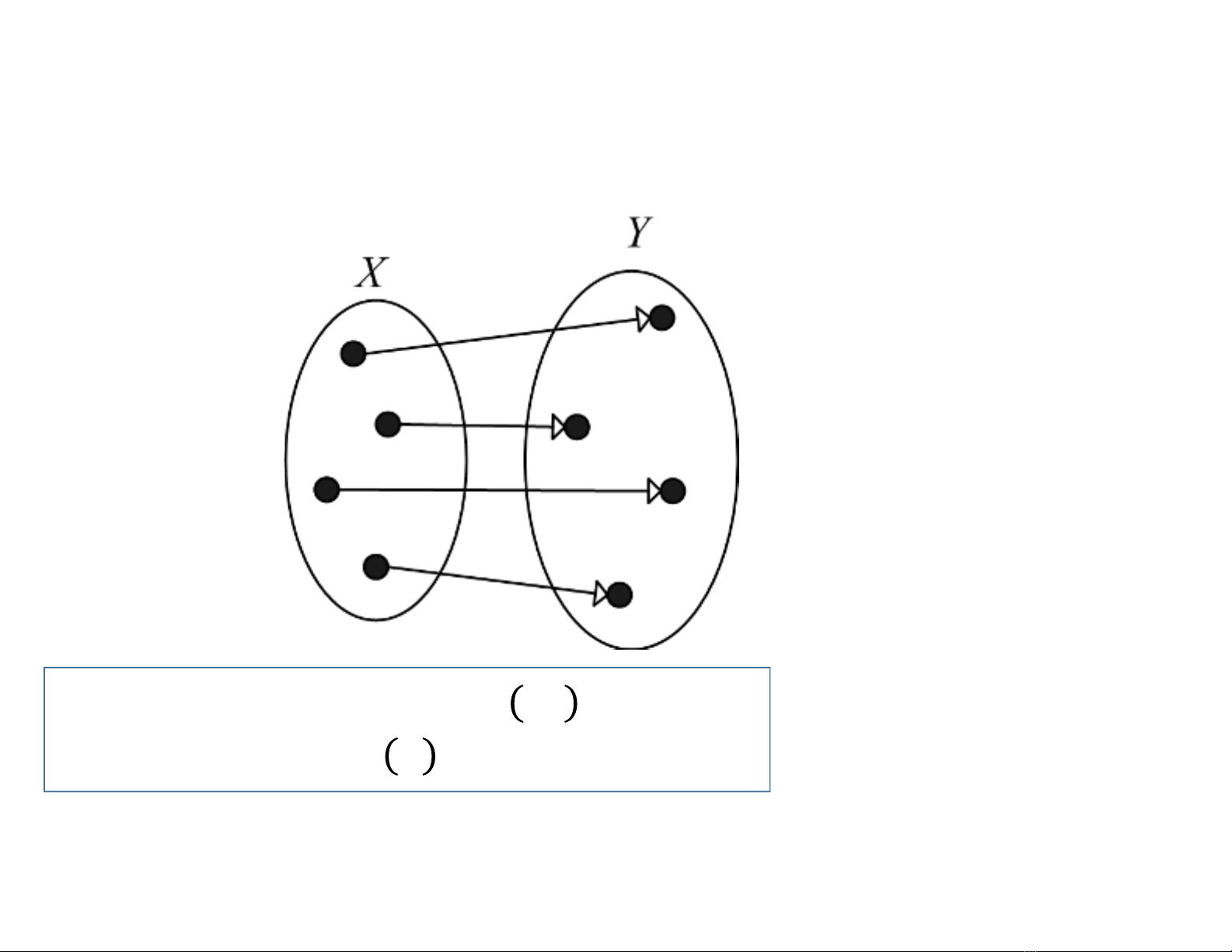
Song ánh (vừa là đơn ánh vừa là toàn ánh).
∀,∈;≠⇒ ≠()
∀∈,∃∈: =
.