§3 : Khả vi và Vi phân
Vi phân cấp 2 là vi phân của vi phân cấp 1
( ) ( )
x y
d f dx d f dy
¢ ¢
= +
2
( ) ( )
x y
d f d df d f dx f dy
¢ ¢
= = +
( ( ) ( )) ( ( ) ( ))
x x y y
d f dx f d dx d f dy f d dy
¢ ¢ ¢ ¢
= + + +
2 2
2
xx xy yy
f dx f dxdy f dy
¢¢ ¢¢ ¢¢
= + +
Hay ta viết dưới dạng
2 2 2
2 2 2
2 2
2
f f f
d f dx dxdy dy
x x y y
¶ ¶ ¶
= + +
¶ ¶ ¶ ¶
Vậy ta viết dưới dạng quy ước sau
2
2
d f dx dy f
x y
æ ö
¶ ¶
÷
ç
= +
÷
ç
÷
ç
è ø
¶ ¶
df dx dy f
x y
æ ö
¶ ¶
÷
ç
= +
÷
ç
÷
ç
è ø
¶ ¶

§3 : Khả vi và Vi phân
2
2
2 2 2
( , , )
2 2 2
xx yy zz xy yz zx
d f x y z dx dy dz f
x y z
f dx f dy f dz f dxdy f dydz f dzdx
æ ö
¶ ¶ ¶ ÷
ç
= + + ÷
ç÷
ç
è ø
¶ ¶ ¶
¢¢ ¢¢ ¢¢ ¢¢ ¢¢ ¢¢
= + + + + +
Vi phân cấp 2 của hàm 3 biến f(x,y,z)
3
3
3 2 2 3
3 3
xxx xxy xyy yyy
d f dx dy f
x y
f dx f dx dy f dxdy f dy
æ ö
¶ ¶ ÷
ç
= + ÷
ç÷
ç
è ø
¶ ¶
¢¢¢ ¢¢¢ ¢¢¢ ¢¢¢
= + + +
Tổng quát công thức trên cho hàm 3 biến và cho vi
phân cấp 3 của hàm 2 biến
Vi phân cấp 3 của hàm 2 biến f(x,y)

§3 : Khả vi và Vi phân
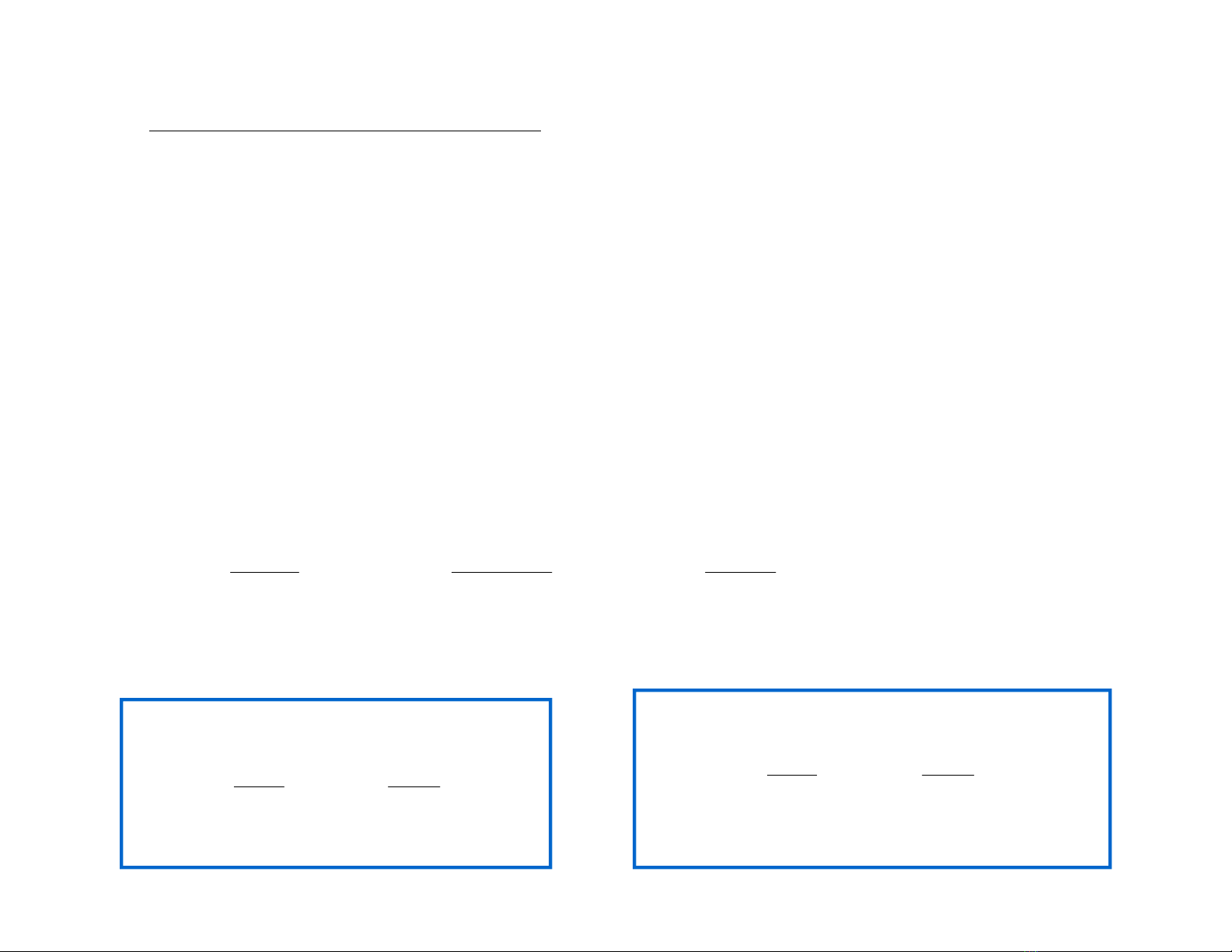
Ví dụ : Cho hàm f(x,y) = xsiny – 2ycosx. Tính df,
d2f tại (0,π/2)
Giải :
Ta đi tính các đạo hàm riêng đến cấp 2, thay vào
công thức tính vi phân
sin 2 sin , cos 2 cos
x y
f y y x f x y x
¢ ¢
= + = -
2 cos , cos 2sin , sin
xx xy yy
f y x f y x f x y
¢¢ ¢¢ ¢¢
= = + = -
(0, ) (0, ) (0, ) 2
2 2 2
x y
df f dx f dy dx dy
p p p
¢ ¢
= + = -
Vậy ta được:
2 2 2
(0, ) (0, ) 2 (0, ) (0, )
2 2 2 2
xx xy yy
d f f dx f dxdy f dx
p p p p
¢¢ ¢¢ ¢¢
= + +
(
)
2 2
0, 2 , à (0, )
2
2
df dx dy v d f dx
p p p= - =
Vậy :
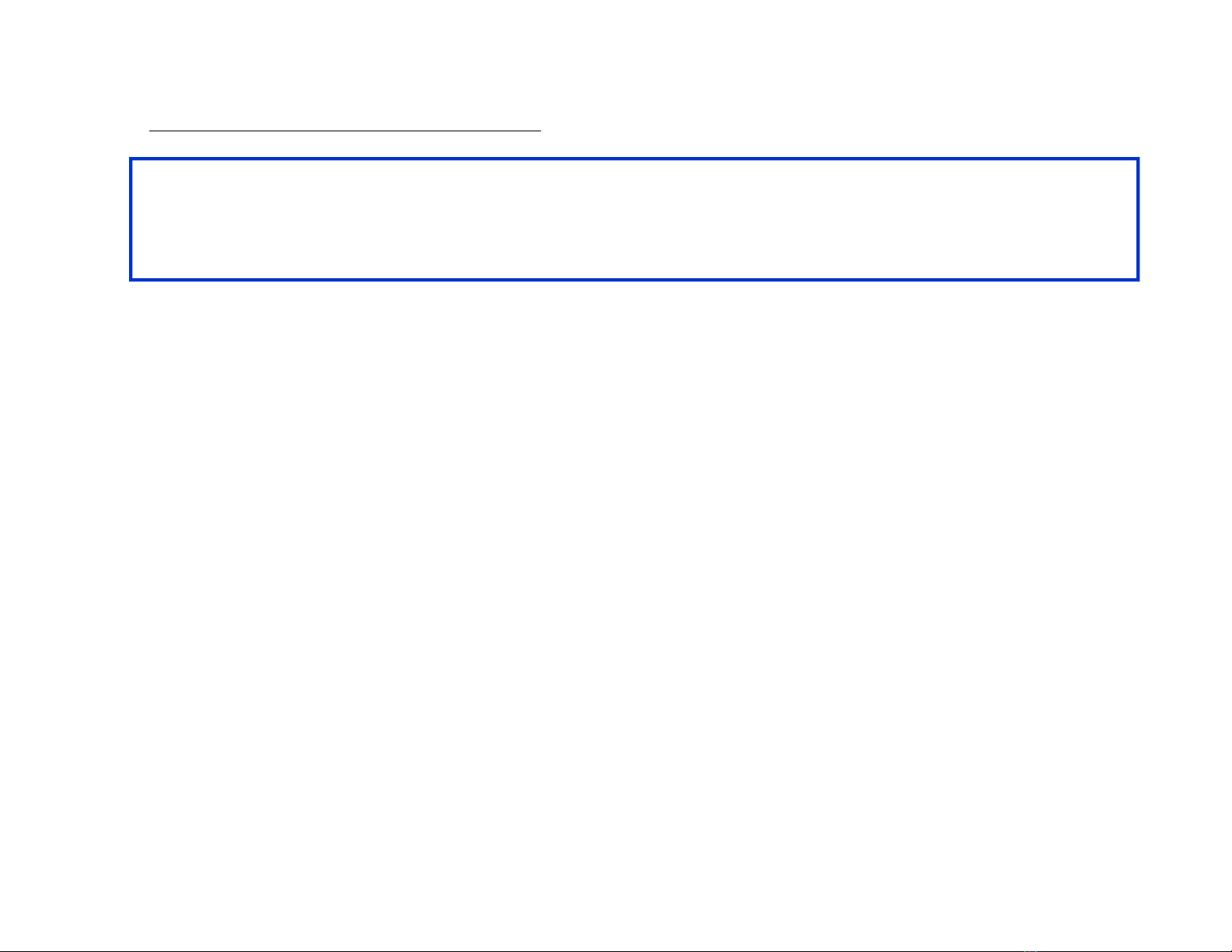
§3 : Khả vi và Vi phân
Ví dụ : Cho hàm f(x,y,z) = xy2– 2yz2 + ex+y+z. Tính
df, d2f
Giải
Tương tự ví dụ trên, ta có
x y z
df f dx f dy f dz
¢ ¢ ¢
= + +
df = (y2+ex+y+z)dx+(2xy–2z2+ex+y+z)dy+(-4yz + ex+y+z)dz
d2f=ex+y+zdx2+(2x+ex+y+z)dy2+ (-4y+ex+y+z) dz2 +
2(2y+ex+y+z)dxdy+2(-4z+ex+y+z)dydz + 2(ex+y+z)dzdx
2 2 2 2 2 2 2
xx yy zz xy yz zx
d f f dx f dy f dz f dxdy f dydz f dzdx
¢¢ ¢¢ ¢¢ ¢¢ ¢¢ ¢¢
= + + + + +
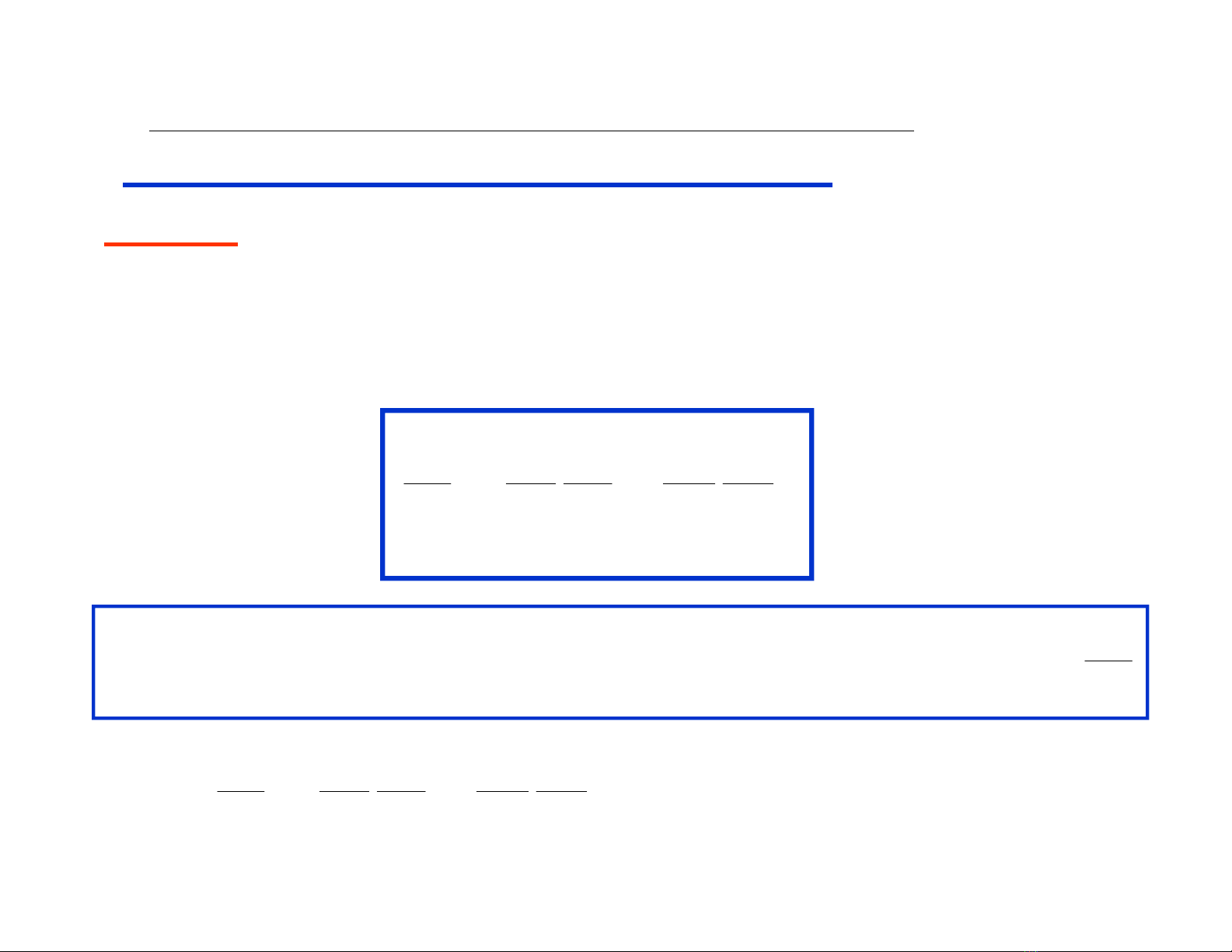
§4 : Đạo hàm riêng và Vi phân hàm hợp
Đạo hàm riêng cấp 1 của hàm hợp
Định lý : Cho hàm z = z(x,y) khả vi trong miền D; x, y
là các hàm theo biến t: x=x(t), y=y(t) khả vi trong
khoảng (t1,t2), khi ấy hàm hợp z = z(x(t),y(t))
cũng
khả vi trong khoảng (t1,t2) và
dz z dx z dy
dt x dt y dt
¶ ¶
= +
¶ ¶
Ví dụ : Cho hàm z = x2-3xy, x = 2t+1, y= t2-3. Tính
dz
dt
Giải:
dz z dx z dy
dt x dt y dt
¶ ¶
= +
¶ ¶ =(2x – 3y)2 + (-3x)2t


























