Bài giảng Nhập môn khai phá dữ liệu: Chương 5 - PGS. TS. Hà Quang Thụy

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:70

Thêm vào BST

Báo xấu

28
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Nhập môn khai phá dữ liệu - Chương 5: Phân lớp. Những nội dung chính trong chương này gồm có: Giới thiệu phân lớp, phân lớp học giám sát, phân lớp học bán giám sát. Mời các bạn cùng tham khảo để biết thêm nội dung chi tiết.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Nhập môn khai phá dữ liệu: Chương 5 - PGS. TS. Hà Quang Thụy

BÀI GIẢNG NHẬP MÔN KHAI PHÁ DỮ LIỆU CHƯƠNG 5. PHÂN LỚP PGS. TS. Hà Quang Thụy HÀ NỘI, 08-2018 TRƯỜNG ĐẠI HỌC CÔNG NGHỆ ĐẠI HỌC QUỐC GIA HÀ NỘI http://uet.vnu.edu.vn/~thuyhq/ Charu C. Aggarwal. Data Classification: Algorithms. CRC Press, 2014. 1
Nội dung Giới thiệu phân lớp Phân lớp học giám sát Phân lớp học bán giám sát 2
Phân lớp: Một vài bài toán ví dụ ⚫ 1. Bài toán phân lớp kết quả xét nghiệm ▪ Miền dữ liệu I = {phiếu xét nghiệm}, ▪ Biến mục tiêu “tập hợp lớp” O = {dương tinh, âm tính} ▪ Ánh xạ f: I → O, f chưa biết ▪ Input: Tập ví dụ mẫu IL gồm phiếu xét nghiệm đã có nhãn dương tình/âm tính. ▪ Output: Ánh xạ xấp xỉ tốt nhất f* để xây dựng chương trình tự động gán nhãn cho mọi phiếu xét nghiệm. ⚫ 2. Bài toán phân lớp cam kết khách hàng ▪ Miền dữ liệu: Tập thông tin mua hàng khách hàng RFM ▪ Mục tiêu “tập hợp lớp” O = {Trung thành cao, Trung thành thấp, Bình thường} ▪ Ánh xạ f: I → O, f chưa biết ▪ Input: Tập ví dụ mẫu IL gồm khách hàng với RFM và nhãn tương ứng. ▪ Output: Ánh xạ xấp xỉ tốt nhất f* để xây dựng chương trình tự động gán nhãn cho mọi khách hàng. 3
Phân lớp: Một vài bài toán ví dụ ⚫ 3. Bài toán phân lớp quan điểm ▪ Miền dữ liệu I = {nhận xét sản phẩm A}, ▪ Mục tiêu “tập hợp lớp” O = {khen, chê} ▪ Ánh xạ f: I → O, f chưa biết ▪ Input: Tập ví dụ mẫu IL gồm đánh giá đã có nhãn khen/chê. ▪ Output: Ánh xạ xấp xỉ tốt nhất f* để xây dựng chương trình tự động gán nhãn cho mọi nhận xét. ⚫ 4. Bài toán phân lớp trang web ▪ Miền dữ liệu: Tập các trang web miền lính vực quan tâm ▪ Mục tiêu “tập hợp lớp” O = {Kinh tế, Thế giới, Thể thao, Giáo dục, v.v.} ▪ Ánh xạ f: I → O, f chưa biết ▪ Input: Tập ví dụ mẫu IL gồm trang web có nhãn thuộc O. ▪ Output: Ánh xạ xấp xỉ tốt nhất f* để xây dựng chương trình tự động gán nhãn cho mọi trang web mới tải về. 4
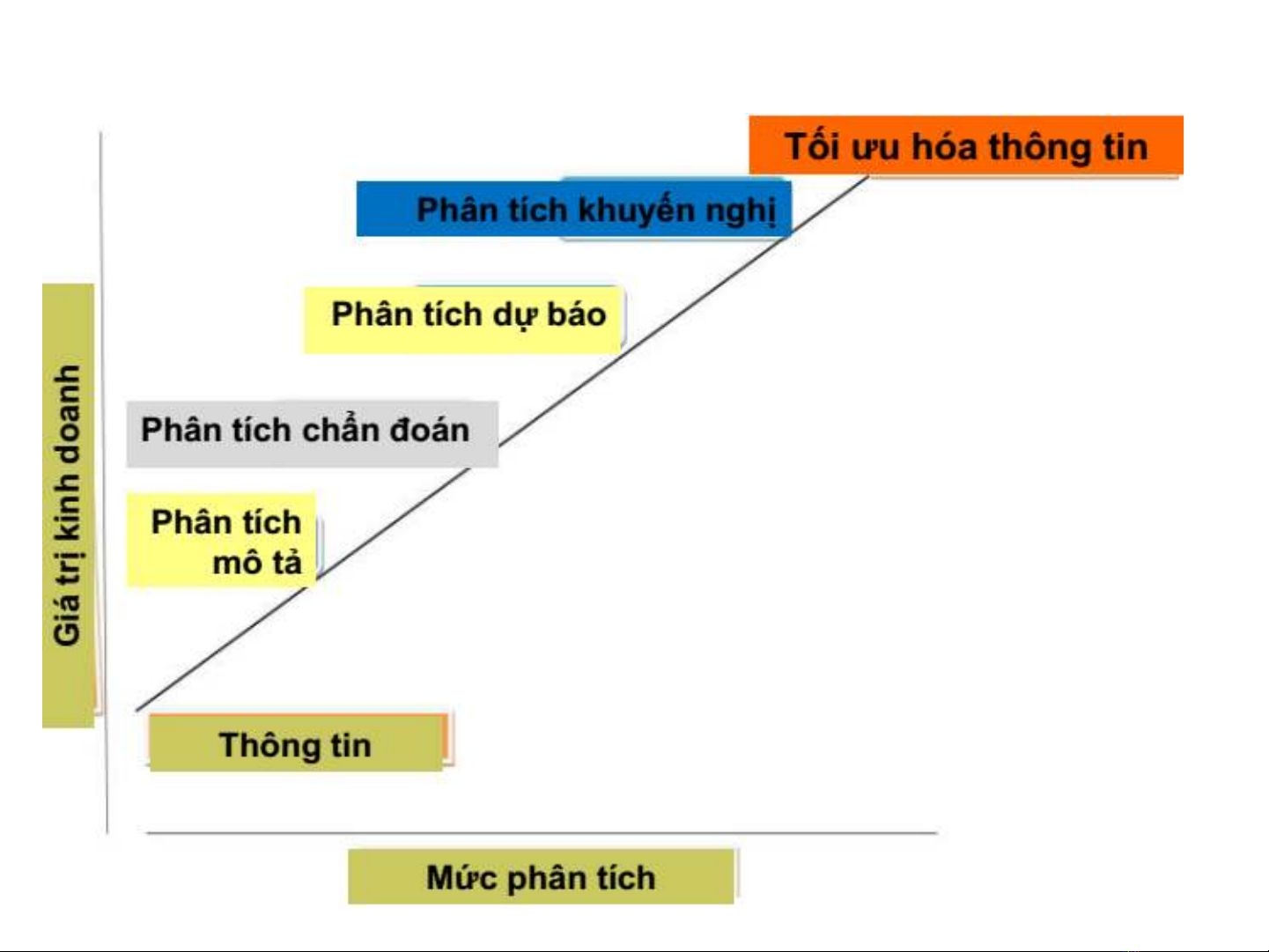
Các mức phân tích kinh doanh Tối ưu hóa thông tin Phân tích khuyến nghị Làm gì khi nó xảy ra một lần nữa? Phân tích dự báoKhi nào nó sẽ xảy ra? PHÂN LỚP Giá trị kinh doanh Phân tích chẩn đoánVì sao điều đó xảy ra? KHAI PHÁ LUẬT KẾT HỢP Phân tích PHÂN CỤM Điều gì đã xảy ra? mô tả - Hiểu sâu sắc thị trường và khách hàng, - Hiểu vận hành nội bộ và nhân viên, - Hiểu giá trị dữ liệu Thông tin 5
2. Học máy giám sát  bài toán tối ưu hóa ⚫ Bốn ví dụ trên đều có thể sử dụng học máy giám sát ⚫ Bài toán học máy giám sát ▪ Cho miền dữ liệu I và một tập nhãn O (hữu hạn) ▪ Tồn tại một ánh xạ f: I → O, f chưa biết Input ▪ Cho “tập ví dụ mẫu” IL: (ILIIL), f xác định trên IL, i IL: f(i)=o đã biết. Output ▪ Tìm ánh xạ toàn bộ f* xấp xỉ tốt nhất f. Bộ phân lớp ⚫ Ví dụ và trao đổi ▪ Miền dữ liệu I = {nhận xét sản phẩm A}, O = {khen, chê} ▪ Ánh xạ f: I → O, f chưa biết ▪ Input: Tập ví dụ mẫu IL gồm đánh giá đã có nhãn khen/chê. ▪ Output: Ánh xạ xấp xỉ tốt nhất f* để xây dựng chương trình 6 tự động gán nhãn cho mọi nhận xét.
Xấp xỉ tốt nhất? ⚫ Biết f chỉ ở một bộ phận (tập IL): f|IL ▪ Thách thức ❖ Tập G vô hạn các ánh xạ, gG, g: I→O ❖ Chưa biết f toàn bộ ▪ Cơ hội: Biết f|IL để chọn f* “xấp xỉ tốt nhất” f ▪ f|IL là toàn bộ “hiểu biết” về f ❖ vừa để tìm ra f* ❖ vừa để kiểm tra tính “tốt nhất” của f* ⚫ Xấp xỉ tốt nhất ▪ Giả thiết: IL “đại diện” cho I; “mọi đặc trưng của I” đều tìm được từ IL. ▪ “đánh giá” cần độc lập với “xây dựng” ▪ IL: vừa tìm f* vừa đánh giá f*. Chia ngẫu nhiên IL = ITrain + ITest. ITrain xây dựng f* và ITest đánh giá f*. ▪ Một số độ đo “tốt” liên quan đến tính “tốt nhất” 7
Bài toán phân lớp ⚫ Đầu vào ⚫ Tập dữ liệu D = {di} ⚫ Tập các lớp C1, C2, …, Ck mỗi dữ liệu d thuộc một lớp Ci ⚫ Tập ví dụ Dexam = D1+D2+ …+ Dk với Di={dDexam: d thuộc Ci} ⚫ Tập ví dụ Dexam đại diện cho tập D ⚫ D gồm m dữ liệu di thuộc không gian n chiều ⚫ Đầu ra ⚫ Mô hình phân lớp: ánh xạ từ D sang C ⚫ Sử dụng mô hình ⚫ d  D \ Dexam : xác định lớp của đối tượng d 8
Phân lớp: Quá trình hai pha ⚫ Xây dựng mô hình: Tìm mô tả cho tập lớp đã có ⚫ Cho trước tập lớp C = {C1, C2, …, Ck} ⚫ Cho ánh xạ (chưa biết) từ miền D sang tập lớp C ⚫ Có tập ví dụ Dexam=D1+D2+ …+ Dk với Di={dDexam: dCi} Dexam được gọi là tập ví dụ mẫu. ⚫ Xây dựng ánh xạ (mô hình) phân lớp trên: Dạy bộ phân lớp. ⚫ Mô hình: Luật phân lớp, cây quyết định, công thức toán học… ⚫ Pha 1: Dạy bộ phân lớp ⚫ Tách Dexam thành Dtrain (2/3) + Dtest (1/3). Dtrain và Dtest “tính đại diện” cho miền ứng dụng ⚫ Dtrain : xây dựng mô hình phân lớp (xác định tham số mô hình) ⚫ Dtest : đánh giá mô hình phân lớp (các độ đo hiệu quả) ⚫ Chọn mô hình có chất lượng nhất ⚫ Pha 2: Sử dụng mô hình (bộ phân lớp) ⚫ d  D \ Dexam : xác định lớp của d. 9
Ví dụ phân lớp: Bài toán cho vay Tid Refund Marital Status Taxable Income Cheat 1 No Single 75K No 2 Yes Married 50K No 3 No Single 75K No 4 No Married 150K Yes 5 No Single 40K No 6 No Married 80K Yes 7 No Single 75K No 8 Yes Married 50K No 9 Yes Married 50K No 10 No Married 150K Yes 11 No Single 40K No 12 No Married 150K Yes 13 No Married 80K Yes 14 No Single 40K No 15 No Married 80K Yes Ngân hàng cần cho vay: trả đúng hạn, hôn nhân, thu nhập 10 “Lớp” liên quan tới cheat (gian lận): hai lớp YES/NO
Phân lớp: Quá trình hai pha 11
Các loại phân lớp – Phân lớp nhị phân/đa lớp Nhị phân: hai lớp (|C| = 2) Đa lớp: số lượng lớp > 2 (|C| > 2) – Phân lớp đơn nhãn/đa nhãn/phân cấp Đơn nhãn: Một đối tượng chỉ thuộc duy nhất một lớp – Đa nhãn: Một đối tượng thuộc một hoặc nhiều lớp – Phân cấp: Lớp này là con của lớp kia 12
3. Đánh giá mô hình phân lớp – Phương pháp đánh giá hiệu quả Câu hỏi: Làm thế nào để đánh giá được hiệu quả của một mô hình? Khách quan – Độ đo đánh giá hiệu quả Câu hỏi: Làm thế nào để có được ước tính đáng tin cậy? Sử dụng các độ đo. Nhiều độ đo: phổ biến – Phương pháp so sánh mô hình Câu hỏi: Làm thế nào để so sánh hiệu quả tương đối giữa các mô hình có tính cạnh tranh? Cùng bộ bộ dữ liệu mẫu, cùng cách đánh giá (bộ độ đo, kịch bản, v.v.) 13
Đánh giá phân lớp nhị phân – Theo dữ liệu test – Giá trị thực: P dương / N âm; Giá trị qua phân lớp: T đúng/F sai. : còn gọi là ma trận nhầm lẫn – Sử dụng các ký hiệu TP (true positives), TN (true negatives), FP (false positives), FN (false negatives) • TP: số ví dụ dương P mà thuật toán phân đúng (T) cho dương P • TN: số ví dụ âm N mà thuật toán phân đúng (T) cho âm N • FN: số ví dụ dương P mà thuật toán phân sai (F) cho âm N - FP: số ví dụ âm N mà thuật toán phân sai (F) cho dương P - Độ hồi tưởng , độ chính xác , các độ đo F1 và F TP TP = = TP + FN TP + FP Đọc thêm: https://www.kdnuggets.com/2020/09/performance-machine- learning-model.html : Các đại lượng ROC, AUC và R2 và https://twitter.com/kdnuggets/status/1301559348993437704 14
Đánh giá phân lớp nhị phân: minh họa R là tập ví dụ kiểm thử được bộ phân lớp gán nhãn dương, L là tập vị dụ kiểm thử thực tế có nhãn dương 15
Đánh giá phân lớp nhị phân – Phương án khác đánh giá mô hình nhị phân theo độ chính xác (accuracy) và hệ số lỗi (Error rate) – Ma trận nhầm lẫn Lớp dự báo Lớp = 1 Lớp = 0 Lớp = 1 f11 f10 Lớp thực sự Lớp = 0 f01 f00 16
So sánh hai phương án – Tập test có 9990 ví dụ lớp 0 và 10 ví dụ lớp 1. Kiểm thử: mô hình dự đoán cả 9999 ví dụ là lớp 0 và 1 ví dụ lớp 1. TP=1 FN = 9 TN=9990 FP= 0 – Theo phương án (recall, precision) có = 1/10=0.1; =1/1=1; f1 = 2*0.1/(0.1+1.0)= 0.18 – Theo phương án (accurary, error rate) có accurary=0.9991; error rate = 9/10000 = 0.0009 Được coi là rất chính xác ! – f1 thể hiện việc đánh giá nhạy cảm với giá dữ liệu 17
Đánh giá phân lớp đa lớp - Bài toán ban đầu: C gồm có k lớp – Đối với mỗi lớp Ci , cho thực hiện thuật toán với các dữ liệu thuộc Dtest nhận được các đại lượng TPi, TFi, FPi, FNi (như bảng dưới đây) Giá trị thực Lớp Ci Không thuộc Thuộc lớp Ci lớp Ci Thuộc lớp Ci Giá trị qua bộ TPi FPi phân lớp đa lớp Không thuộc FNi TNi lớp Ci 18
Đánh giá phân lớp đa lớp ⚫ Tương tự bộ phân lớp hai lớp (nhị phân) ⚫ Độ chính xác Pri của lớp Ci là tỷ lệ số ví dụ dương được thuật toán phân lớp cho giá trị đúng trên tổng số ví dụ được thuật toán phân lớp vào lớp Ci : TPi Pri = TPi + FPi ⚫ Độ hồi tưởng Rei của lớp Ci là tỷ lệ số ví dụ dương được thuật toán phân lớp cho giá trị đúng trên tổng số ví dụ dương thực sự thuộc lớp Ci: TPi Re i = TPi + FN i 19
Đánh giá phân lớp đa lớp - Các giá trị i và i : độ hồi phục và độ chính xác đối với lớp Ci. - Đánh giá theo các độ đo - trung bình mịn (micro – average, được ưa chuộng)  và  - trung bình thô (macro- average) M và M K 1  M = K  c M 1 K =  c c =1 K c =1   cK=1TPc  cK=1TPc  = K  = K  c =1 (TPc + FN c ) c =1 (TPc + FN c ) 20