Bài giảng Tin học đại cương: Bài 5 - ĐH Bách khoa Hà Nội

Chia sẻ: Khang Duy | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

134
lượt xem 13
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài 5 Một số thuật toán thông dụng thuộc bài giảng "Tin học đại cương", cùng nắm kiến thức trong chương này thông qua các các nội dung sau: các cấu trúc cơ bản trong lập trình, giải mã (pseudocode), thuật toán số học, thuật toán về dãy, thuật toán đệ quy.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Tin học đại cương: Bài 5 - ĐH Bách khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI Nội dung VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG 5.1. Các cấu trúc cơ bản trong lập trình 5.2. Giả mã (pseudocode) TIN HỌC ĐẠI CƯƠNG 5.3. Thuật toán số học Phần 2. Giải quyết bài toán 5.4. Thuật toán về dãy 5.5. Thuật toán đệ quy Bài 5: Một số thuật toán thông dụng 2 5.1. Các cấu trúc cơ bản trong lập trình 5.1.1. Cấu trúc tuần tự • Cấu trúc tuần tự • Các bước được thực hiện theo 1 trình tự tuyến tính, hết bước này đến bước khác • Cấu trúc rẽ nhánh • Cấu trúc lặp Bước 1 Bước 2 … Bước n 3 4 1
5.1.2. Cấu trúc rẽ nhánh 5.1.3. Cấu trúc lặp • Việc thực hiện bước nào phụ thuộc vào điều kiện • Một tác động/ nhiệm vụ xác định. có thể được thực hiện lặp • Ví dụ: Tìm max của 2 số a, b. nhiều lần. Điều kiện – Nếu a > b thì max là a, ngược lại max sẽ là b. • Số lần lặp có thể biết – Diễn giải: trước hoặc không biết • B1: Nhập 2 số a, b. trước.Tuy nhiên số lần • B2: Nếu a > b thì Max = a và đi đến bước kết thúc (B4). • B3: (a b S Max  a Max  b Thực hiện công việc khi thoát khỏi vòng lặp 5 6 5.1.3. Cấu trúc lặp (2) Nội dung Ví dụ: Tìm số lớn nhất của Nhập N và 5.1. Các cấu trúc cơ bản trong lập trình dãy số a1, a2,…,aN một dãy có n số 5.2. Giả mã (pseudocode)  Lần lượt phải so sánh số Max Max  a1; i=2 tạm thời (lúc đầu Max được 5.3. Thuật toán số học gán bằng phần tử thứ nhất, a1) với ai, với i từ 2, 3,…, n. Đ Hiển thị 5.4. Thuật toán về dãy i>N “Max là số lớn nhất” Việc so sánh này được thực  hiện lặp nhiều lần giữa Max 5.5. Thuật toán đệ quy S và ai. Đ  Khi kết thúc quá trình lặp, ta ai > Max Max  ai sẽ thu được Max là số lớn nhất của dãy n số. S ii+1 7 8 2
5.2. Mã giả (pseudocode) 5.2. Giả mã (2) • Gán:  hoặc := • Cấu trúc lặp: while điều_kiện do hành_động Ví dụ: i  i + 1 hoặc a := b + c repeat • Cấu trúc rẽ nhánh hành_động if(điều kiện) then (hành động) until điều_kiện hoặc hoặc for biến:= gtrị_đầu to gtrị_cuối do hành_động if(điều kiện) then (hành động) hoặc else (hành động) for biến:= gtrị_đầu downto gtrị_cuối do hành_động • Cấu trúc nhảy goto: – goto nhãn x; 9 10 Nội dung 5.3. Thuật toán số học 5.1. Các cấu trúc cơ bản trong lập trình • Các bài toán về số học 5.2. Giả mã (pseudocode) – Xác định một số nguyên có phải là số nguyên tố/hợp số hay không 5.3. Thuật toán số học – Tìm USCLN, BSCNN của 2 số nguyên 5.4. Thuật toán về dãy – .. 5.5. Thuật toán đệ quy 11 12 3
Bài toán số nguyên tố Bài toán số nguyên tố (2) Nhập p • Cho một số nguyên dương p. Làm thế nào để biết if p=1 then begin được p có phải số nguyên tố hay không? Xuất: p không nguyên tố; – Input: p nguyên dương Dừng thuật toán; – Output: kết luận về tính nguyên tố của p end flag := TRUE //Cờ trạng thái cho biết có tìm được ước nào của p không • Ý tưởng? for k:=2 to p-1 do //Tối ưu duyệt đến [căn bậc 2 của p] – p = 1?  Không phải số nguyên tố if (k là ước số của p) then – p > 1? begin • Kiểm tra từ 2 đến p-1 có phải là ước số của p không flag:=FALSE break //ngắt vòng lặp FOR • Nếu có thì kết luận p không là số nguyên tố, ngược lại end không có số nào thì kết luận p là số nguyên tố if flag=TRUE then Xuất: p là số nguyên tố else 13 14 Xuất: p không là số nguyên tố Nội dung 5.4. Thuật toán về dãy 5.1. Các cấu trúc cơ bản trong lập trình • Làm việc với một dãy số 5.2. Giả mã (pseudocode) • Các bài toán điển hình 5.3. Thuật toán số học – Tìm số lớn nhất, nhỏ nhất trong dãy 5.4. Thuật toán về dãy – Kiểm tra dãy có phải là dãy tăng hoặc dãy giảm – Sắp xếp dãy tăng dần hoặc giảm dần 5.5. Thuật toán đệ quy – Tìm trong dãy có phần tử nào bằng một giá trị cho trước – Tính trung bình cộng của dãy –… 15 16 4
Ví dụ 1 - Tìm số lớn nhất trong dãy Ví dụ 2. Sắp xếp dãy số • Input: dãy số a1, a2, a3,… an • Bài toán: Sắp xếp bằng phương pháp nổi bọt • Output: max là giá trị lớn nhất trong dãy số (Bubble Sort) đã cho – Đầu vào: Dãy A gồm N số nguyên a1, a2,…, aN • Thuật toán: – Đầu ra: Dãy A được sắp lại theo thứ tự không giảm. • Ý tưởng: max:=a1 – Với mỗi cặp số liên tiếp trong dãy, nếu số trước lớn hơn for i:=2 to n do số sau ta đổi chỗ chúng cho nhau. 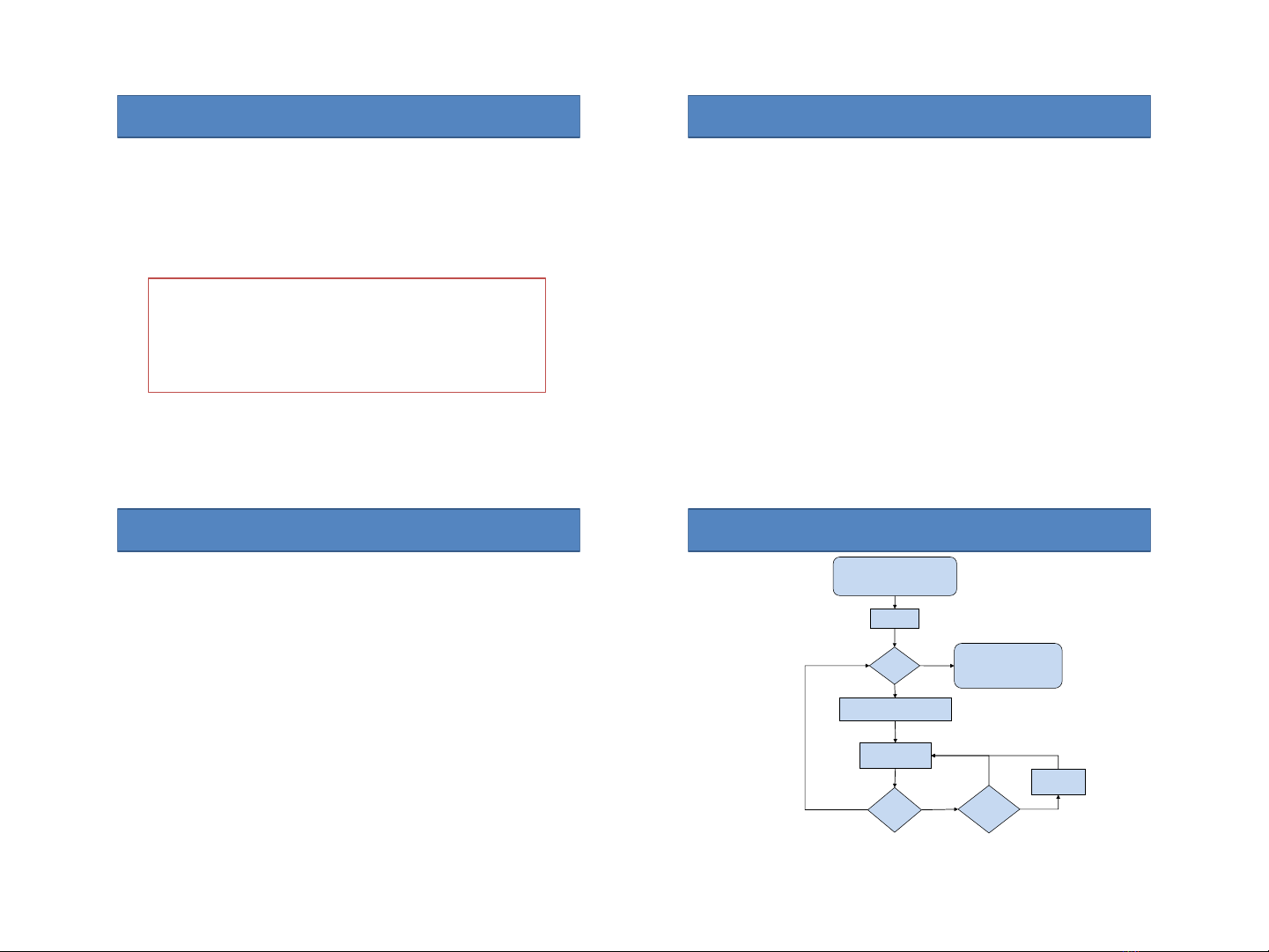if max < ai then max:= ai – Việc đó được lặp cho đến khi không có sự đổi chỗ nào Xuất: max là giá trị lớn nhất trong dãy số cho nhau 17 18 Ví dụ 2 - Mô tả tuần tự các bước Ví dụ 2 - Mô tả bằng lưu đồ thuật toán Nhập N và dãy số a1, a2,…,aN • B1: Nhập số N và dãy số a1,a2,…,aN • B2: M  N. MN • B3: Nếu M < 2 thì thuật toán kết thúc và hiển thị Đ Hiển thị dãy đó. M M thì quay lại B3. ii+1 • B7: Nếu ai > ai+1 thì tráo đổi hai số đó cho nhau S ai  ai+1 • B8: Quay lên B5. Đ S i>M ai > ai+1 Đ 19 20 5
Bài tập Nội dung • Bài 1. Xây dựng thuật toán tìm phần tử có giá trị truyệt đối 5.1. Các cấu trúc cơ bản trong lập trình lớn nhất trong dãy gồm n phần tử. • Bài 2. Xây dựng thuật toán tìm tổng của các số chẵn và tổng 5.2. Giả mã (pseudocode) của các số lẻ trong dãy gồm n phần tử được nhập vào từ 5.3. Thuật toán số học bàn phím. • Bài 3. Xây dựng thuật toán kiểm tra xem một dãy số gồm n 5.4. Thuật toán về dãy phần tử được nhập vào từ bàn phím có phải là dãy số tăng 5.5. Thuật toán đệ quy (hoặc giảm) không. • Bài 4. Xây dựng thuật toán tính trung bình cộng của các số dương trong dãy gồm n số được nhập vào từ bàn phím. 21 22 5.5. Thuật toán đệ quy 5.5. Thuật toán đệ quy (2) • Với bài toán có thể được phân tích và đưa • Để xây dựng thuật toán đệ quy, cần xác định: tới việc giải một bài toán cùng loại nhưng – Trường hợp cơ bản: (Các) trường hợp không cần thực hiện lại thuật toán. cấp độ thấp hơn – Phần tổng quát: Có yêu cầu gọi đệ quy – độ lớn dữ liệu nhập nhỏ hơn • Cần xác định nguyên lý đưa trường hợp tổng quát về – giá trị cần tính toán nhỏ hơn trường hợp cơ bản  Tự thực hiện lại thuật toán • Đảm bảo tính dừng của giải thuật đệ quy - chắc chắn từ trường hợp tổng quát sẽ đến được trường hợp cơ • Ví dụ: bản – Giai thừa: n! = (n-1)! * n – Dãy số Fibonacci: 0, 1, 1, 2, 3, 5, 8... • F(n) = F(n-1) + F(n-2) 23 24 6
Ví dụ Tính giai thừa - Thuật toán đệ quy • Tính giai thừa của n: • Input: số tự nhiên n – Trường hợp cơ bản: 0! = 1 • Output: GT(n)=n! – Trường hợp tổng quát: n! = (n-1)! * n • Thuật giải: • Xây dựng dãy Fibonacci Nhập n – Trường hợp cơ bản: F(0) = F(1) = 1 GT:=1; – Trường hợp tổng quát: F(n) = F(n-1) + F(n-2) if n>0 then GT := GT(n-1)*n; Xuất GT 25 26 Bài tập Thuật giải heuristic • Xây dựng thuật toán cho bài toán tìm số • Dùng “mẹo” Fibonacci F(n) • Áp dụng với những bài toán – Chưa tìm được thuật toán và không biết có tồn tại thuật toán không – Có thuật toán nhưng thời gian tính toán quá lâu hoặc điều kiện của thuật toán khó đáp ứng 27 28 7