Giảng viên: ThS. Trần Quang Khải
TOÁN RỜI RẠC
Chương 6:
Đồ thị
Toán rời rạc: 2011-2012
Nội dung (phần 3)
1. Bài toán tìm đường đi ngắn nhất:
Giải thuật Dijsktra.
2. Giới thiệu bài toán TSP.
Chương 6: Đồ thị 2
Toán rời rạc: 2011-2012
Giảng viên: ThS. Trần Quang Khải
Bài toán tìm đường đi
ngắn nhất
Chương 6
Toán rời rạc: 2011-2012
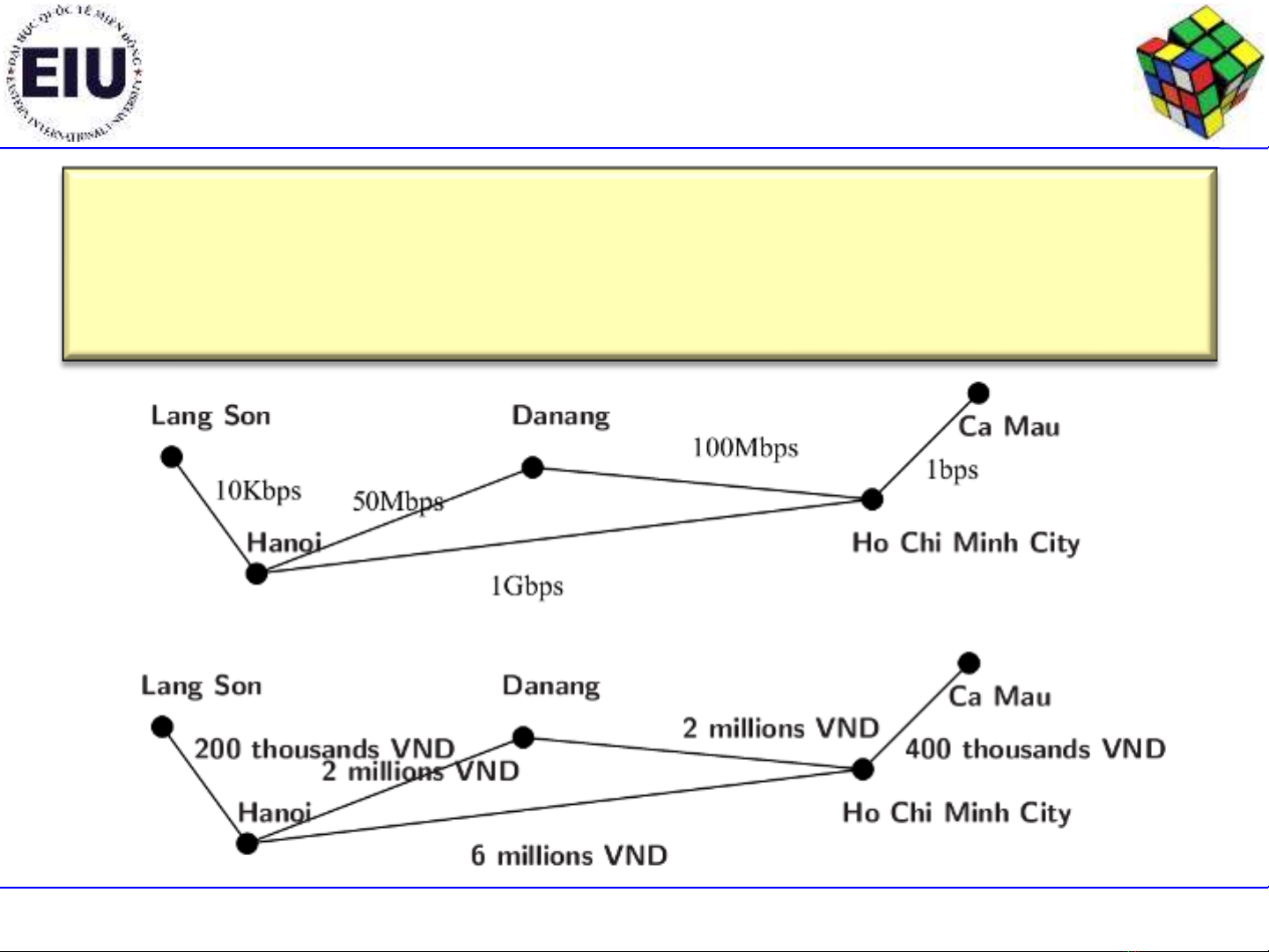
Đồ thị có trọng số
Chương 6: Đồ thị 4
Weighted graph
Là đồthịmà mỗi cạnh được gán một số(nguyên
hoặc thực) với ngụý nào đó.
Toán rời rạc: 2011-2012
Đồ thị có trọng số
Liên quan:
Thời gian.
Khoảng cách.
Chi phí.
…
Chương 6: Đồ thị 5