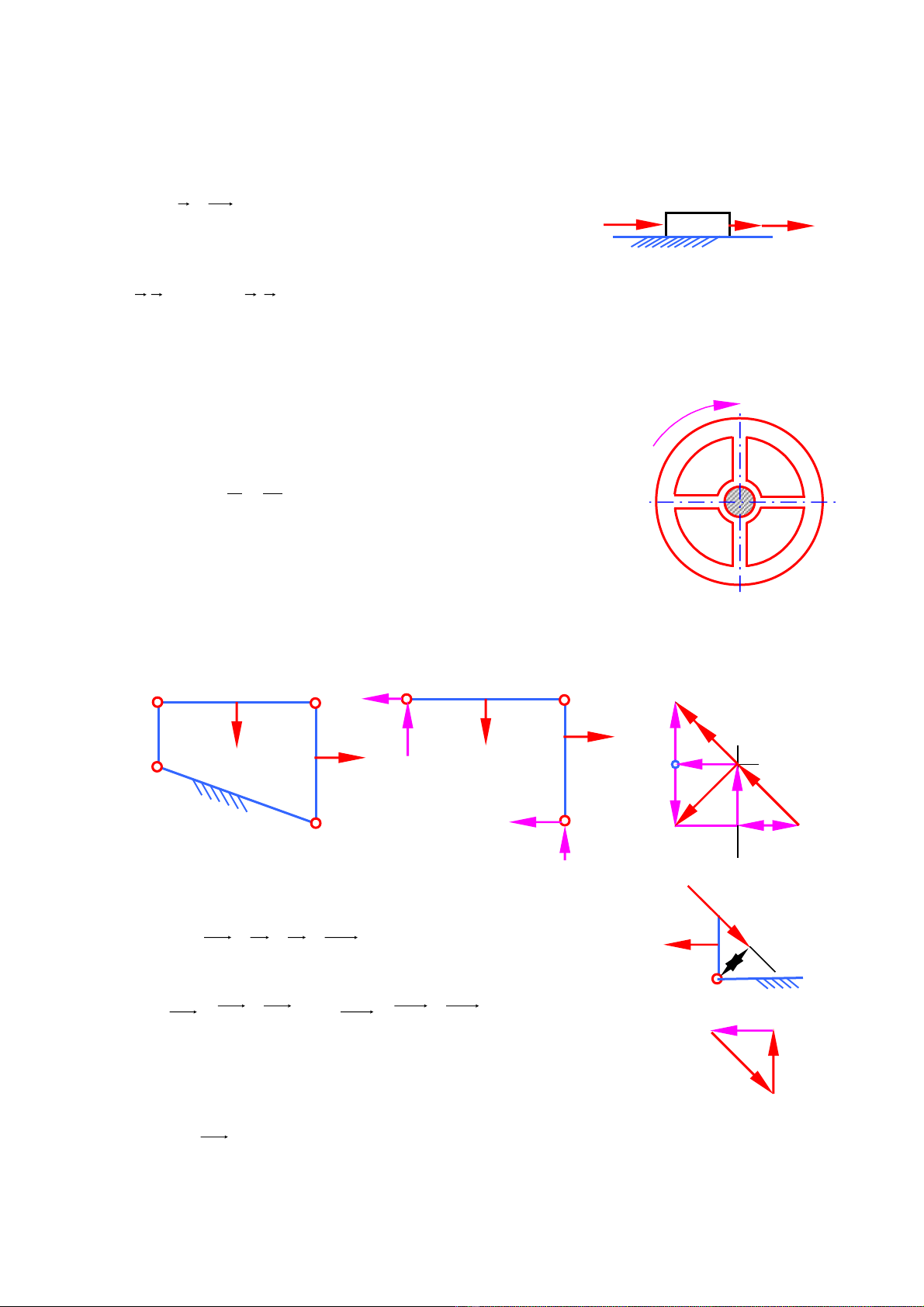
CH NG 3: PHÂN TÍCH L C H C TRÊN C C U PH NG LO I 2ƯƠ Ự Ọ Ơ Ấ Ẳ Ạ
1) M t con tr t chuy n đ ng nhanh d n v i gia t c a = 10m/sộ ượ ể ộ ầ ớ ố 2. Không k t i ma sát trên m tể ớ ặ
tr t, tính công su t ngo i l c P đ y v t chuy n đ ng khi v t có v n t c 5m/s. Bi t kh iượ ấ ạ ự ẩ ậ ể ộ ậ ậ ố ế ố
l ng c a con tr t là m = 2 kg (hình 3.1).ượ ủ ượ
Áp d ng nguyên lý D A lăm be, thu đ c:ụ ượ
0=+ qt
PP
Pqt = m.a = 2.10 = 20N.
P = 10N
Công su t ngo i l c P đ y v t chuy n đ ng v i v n t c 5m/s: Hình 3.1ấ ạ ự ẩ ậ ể ộ ớ ậ ố
WVPVPVP 1005.20),cos(.. ===
2) Hãy tính mômen c a l c quán tính c a bánh đà trong th i gian m máy: Bi t lúc b t đ u mủ ự ủ ờ ở ế ắ ầ ở
máy v n t c góc b ng 0 và sau 3 giây v n t c tăng t l v i th i gian thì máy chuy n đ ngậ ố ằ ậ ố ỷ ệ ớ ờ ể ộ
bình n, v i v n t c góc trung bình ổ ớ ậ ố ω = 21s-1; mômen quán tính c a bánh đà là J = 2kg.mủ2,
tr ng tâm c a bánh đà ngay trên tr c quay (hình 3.2)ọ ủ ở ụ
Ph ng trình chuy n đ ng c a bánh đà:ươ ể ộ ủ
t
εω
=
2
/7
3
21 srad
t===
ω
ε
Mômen c a l c quán tính đ c tính:ủ ự ượ
M = J . ε = 2 . 7 = 14Nm
Hình 3.2
3) Tính nh ng áp l c kh p đ ng và l c cân b ng (đ t t i đi m gi a khâu AB theo ph ngữ ự ớ ộ ự ằ ặ ạ ể ữ ươ
vuông góc v i khâu này), cho tr c lớ ướ AB = 0,1m, lBC = lCD = 0,2m. L c c n Pự ả 2 = P3 = 1000N tác
đ ng t i trung đi m các khâu. L c c n Pộ ạ ể ự ả 2 h ng th ng đ ng xu ng d i, l c Pướ ẳ ứ ố ướ ự 3 h ng n mướ ằ
ngang sang ph i nh hình 3.3a. AB, CD th ng đ ng, BC n m ngangả ư ẳ ứ ằ
Hình 3.3a Hình 3.3b Hình 3.3c
Tách nhóm tĩnh đ nh BCD và đ t l c vào các kh p ch (hình 3.3b):ị ặ ự ớ ờ
R12 và RD3. Vi t ph ng trình cân b ng l c cho toàn nhóm:ế ươ ằ ự
0
33212
=+++
D
RPPR
(1)
ph ng trình (1) t n t i 4 n s : Giá tr và ph ng chi u c a 2 l c:ươ ồ ạ ẩ ố ị ươ ề ủ ự
R12 và RD3. Chia các áp l c này ra thành 2 thành ph n (hình 3.3b)ự ầ
τ
1212
12 RRR n+=
và
τ
33
3D
n
D
DRRR +=
L y t ng mômen c a các l c đ i v i đi m C thu c khâu 2 và thu c khâu 3:ấ ổ ủ ự ố ớ ể ộ ộ
0..)( 2
12
)( 2=−=Σ MCBCiC lPlRRM
τ
Hình 3.3d
Chi u ề
τ
12
R
đã ch n ban đ u là đúng.ọ ầ
0..)( 3
3
)( 3=−=Σ NCCD
D
iC lPlRRM
τ
P
V
a
ω
A
BC
D
M
N
P2
P3
B
C
D
M
N
P2
P3
τ
12
R
n
R12
τ
3D
R
n
D
R3
a
b
c
d
e
f
A
B
R21
Pcb
h
1
2
3
2
3
1
R21
Pcb
RA1
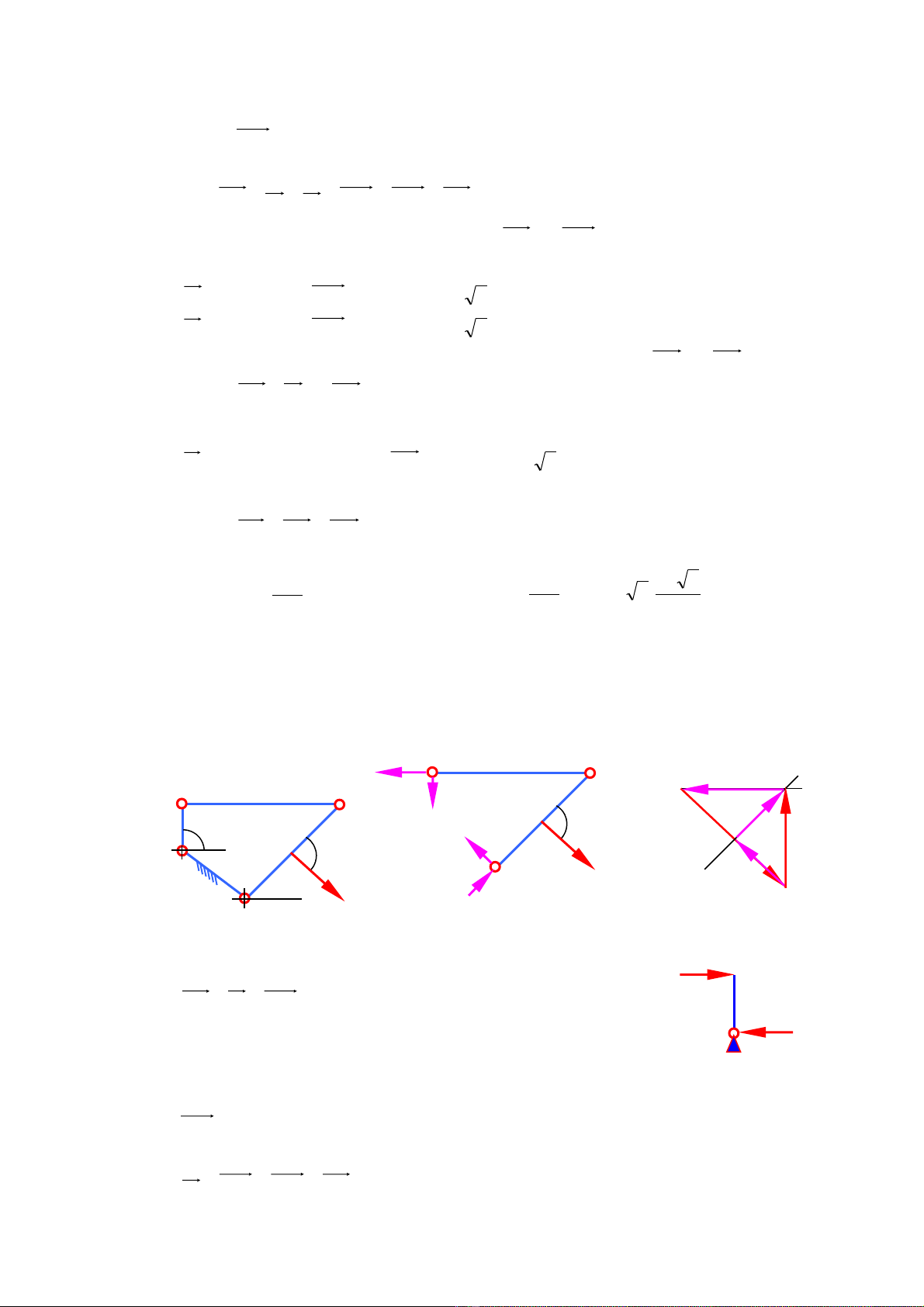
05005,0 3
3〉== NPRD
τ
Chi u ề
τ
3D
R
đã ch n ban đ u là đúng.ọ ầ
Vi t l i ph ng trình cân băng l c (1):ế ạ ươ ự
0
1233
32
12 =+++++ nn
DD RRRPPR
ττ
(2)
Ph ng trình (2) ch còn t n t i 2 n s là giá tr c a ươ ỉ ồ ạ ẩ ố ị ủ
n
R12
và
n
D
R3
. Cách gi i đ c trình bày trênả ượ
hình 3.3c.
Véc t ơ
df
bi u th áp l c ể ị ự
3D
R
có giá tr là ị
)(2500 N
, có chi u nh hình v 3.3cề ư ẽ
Véc t ơ
fb
bi u th áp l c ể ị ự
3D
R
có giá tr là ị
)(2500 N
, có chi u nh hình v 3.3cề ư ẽ
Vi t ph ng trình cân băng l c riêng cho khâu 2 đ tính áp l c t i kh p C: ế ươ ự ể ự ạ ớ
3223 RR −=
0
32212 =+++ RPR
(3)
Ph ng trình này ch t n t i 2 n s là giá tr và ph ng chi u c a Rươ ỉ ồ ạ ẩ ố ị ươ ề ủ 32. cách gi i đ c v hìnhả ượ ẽ ở
3.3c.
Véc t ơ
fc
bi u th áp l c t i kh p C ể ị ự ạ ớ
32
R
có giá tr là ị
)(2500 N
, chi u nh hình v 3.3c.ề ư ẽ
Bây gi ta đi tính l c cân b ng đ t t i đi m gi a khâu AB:ờ ự ằ ặ ạ ể ữ
Ph ng trình cân băng l c c a khâu 1:ươ ự ủ
0
121 =++ Acb RRP
(4)
Ph ng trình này t n t i 3 n s , đ làm gi m b t n s , ta đi tìm giá tr Pươ ồ ạ ẩ ố ể ả ớ ẩ ố ị cb:
0.
2
.)( 21)( =−=Σ hR
l
PRM AB
cbiA
N
l
h
RP
AB
cb 500.
1,0.2
21,0
2500.2.2 21 ===
Ph ng trình 4 đ c gi i hình 3.3d, và ph ng chi u c a Rươ ượ ả ở ươ ề ủ A1 đ c bi u di n nh hình v , giá trượ ể ễ ư ẽ ị
đ c tính b ng 500Nượ ằ
4) Tính nh ng áp l c kh p đ ng và moomen cân b ng trên khâu d n 1 c a c c u 4 khâu b nữ ự ớ ộ ằ ẫ ủ ơ ấ ả
l ph ng; cho tr c lề ẳ ướ AB = lBC / 4 = lCD / 4 = 0,1m; khâu BC n m ngang; các góc ằϕ1 = 90o, ϕ2 =
45o và l c c n Pự ả 3 = 1000N tác đ ng t i trung đi m khâu 3 v i ộ ạ ể ớ α3 = 90o (hình 3.4a). Xét xem
vi c tính nh ng áp l c kh p đ ng y có ph thu c và v n t c góc khâu d n không? Gi iệ ữ ự ớ ộ ấ ụ ộ ậ ố ẫ ả
thích?
Hình 3.4a Hình 3.4b Hình 3.4c
Tách nhóm tĩnh đ nh và đ t các áp l c t i kh p ch . ị ặ ự ạ ớ ờ
Ph ng trình cân b ng l c đ c vi t cho toàn nhóm:ươ ằ ự ượ ế
0
3312 =++ D
RPR
(1)
Chia áp l c t i kh p ch ra làm 2 thành ph n nh hình v (hình 3.4b):ự ạ ớ ờ ầ ư ẽ
0.)( 12
)( 2==Σ BCiC lRRM
τ
0
12 =
τ
R
0..)( 3
3
)( 3=−=Σ MCCD
D
iC lPlRRM
τ
05005,0 3
3〉== NPRD
τ
Hình 3.4d
Chi u ề
τ
3D
R
đã ch n ban đ u là đúngọ ầ
Ph ng trình cân b ng l c (1) đ c vi t l i nh sau:ươ ằ ự ượ ế ạ ư
0
1233
3=+++ nn
DD RRRP
τ
(2)
A
BC
D
M
P3
123
ϕ1
ϕ2
α3
BC
D
M
P3
23
α3
n
R
12
n
D
R
3
τ
12
R
τ
3D
R
a
b
c
d
A
B
R21
RA1
Mcb
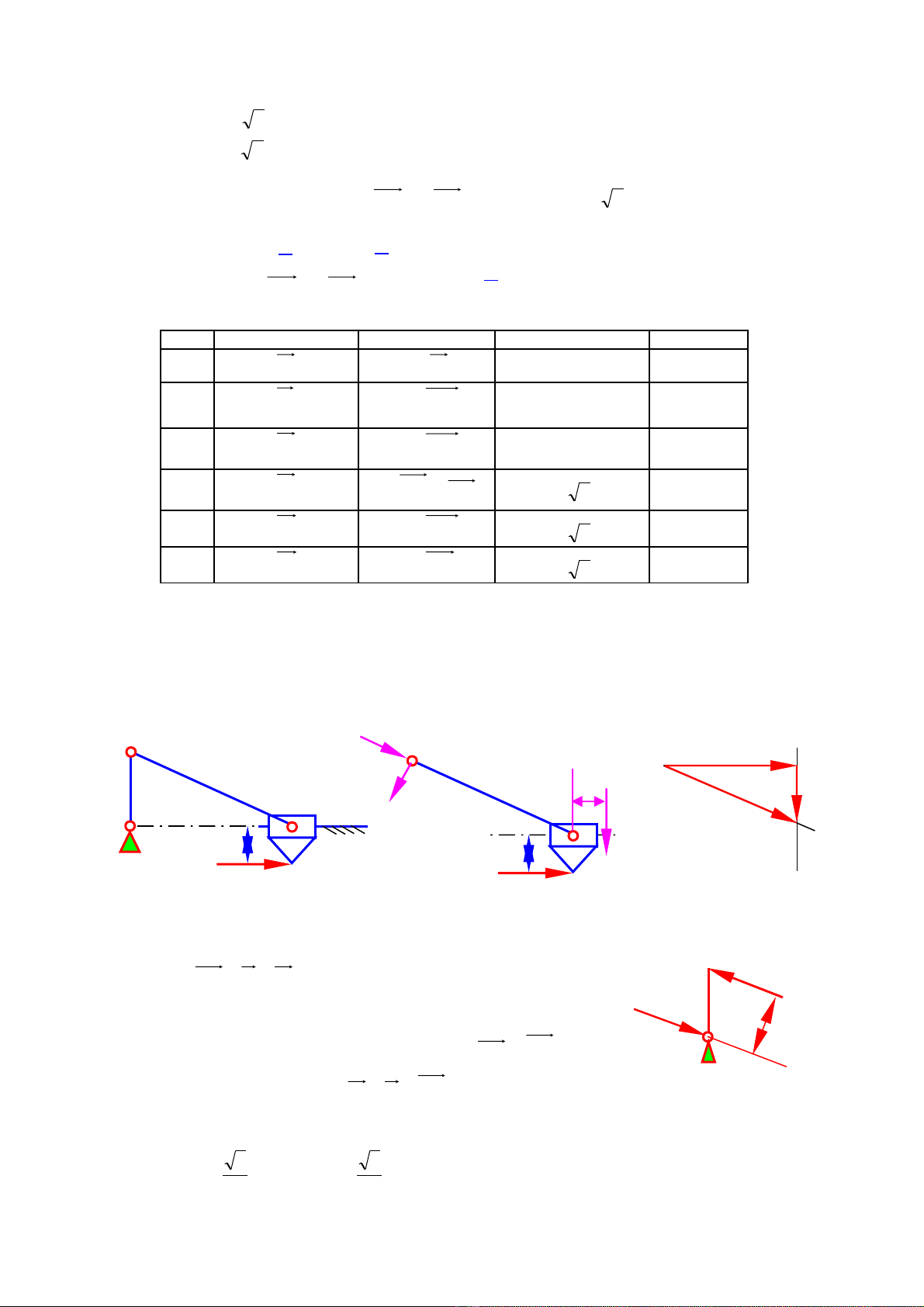
Ph ng trình (2) ch t n t i 2 n s , ho đ l c đ c v nh hình 3.4c.ươ ỉ ồ ạ ẩ ố ạ ồ ự ượ ẽ ư ở
NRD2500
3=
, chi u đ c xác đ nh nh hình về ượ ị ư ẽ
NR 2500
12 =
, chi u cũng đ c xác đ nh nh hình v .ề ượ ị ư ẽ
Tính áp l c t i kh p trong C:ự ạ ớ
Xét s cân b ng c a khâu 2: ự ằ ủ
1232
RR −=
, giá tr :ị
NR 2500
32 =
Tính mômen cân bbawnoo đ t trên khâu d n 1:ặ ẫ
Ch n chi u Mọ ề cb nh hình 3.4d.ư
Mcb = R21 . lAB = 500√ 2 . 0,1 = 50√ 2 Nm
Áp l c t i kh p A: ự ạ ớ
211 RRA−=
, giá tr b ng 500ị ằ √ 2 N
Ta l p b ng so sánh:ậ ả
TT Véc t bi u di nơ ể ễ Véc t th tơ ậ Giá trịGhi chú
1
ab
3
P
1000N
2
bc
τ
3D
R
500N
3
cd
n
D
R3
500N
4
da
12
12 RRn=
N2500
5
bd
3D
R
N2500
6
ad
32
R
N2500
Các giá tr trên khi tính không ph thu c vào v n t c góc c a khâu d n, b i vì chúng ta không đi xácị ụ ộ ậ ố ủ ẫ ở
đ nh l c quán tínhị ự
5) Tính nh ng áp l c kh p đ ng và moomen cân b ng trên khâu d n 1 c a c c u tay quay conữ ự ớ ộ ằ ẫ ủ ơ ấ
tr t (hình 3.5a), cho tr c lượ ướ AB = lBC / 2 = 0,1m, AB th ng đ ng, AC n m ngang. L c c n Pẳ ứ ằ ự ả 3 =
1000N n m ngang cách rãnh tr t m t đo n hằ ượ ộ ạ 3 = 0,058m. Sau đó nghi m l i K t qu Mệ ạ ế ả cb
b ng ph ng pháp công su t.ằ ươ ấ
Hình 3.5a Hình 3.5b Hình 3.5c
Tách nhóm tĩnh đ nh ra kh i c c u và đ t áp l c vào các kh p ch (hình 3.5b):ị ỏ ơ ấ ặ ự ớ ờ
Ph ng trình cân b ng l c đ c vi t:ươ ằ ự ượ ế
0
312 =++ PNR
(1)
Ph ng trình (1) có 3 n s , ta c n ph i gi m b t các n s .ươ ẩ ố ầ ả ả ớ ẩ ố
Chia áp l c kh p ch B ra làm 2 thành ph n (hình 3.5b):ự ở ớ ờ ầ
0.)( 12
)( 2==Σ BCiC lRRM
τ
0
12 =
τ
R
n
RR 12
12 =
Ph ng trình (1) đ c vi t l i: ươ ượ ế ạ
0
12
3=++ n
RNP
(2) Hình 3.5d
Ho đ l c đ c v nh hình 3.5c.ạ ồ ự ượ ẽ ư ở
Do tam giác ABC là n a tam giác đ u nên tam giác abc trên hình 3.5c cũng là n a tam giác đ u:ử ề ử ề
NR 3
3
2000
12 =
,
NN 3
3
1000=
Chi u c a các l c đã ch n ban đ u là phù h p.ề ủ ự ọ ầ ợ
A
B
C
1
2
3
P3
h3
R12
nN
P3
a
b
c
B
C
2
3
P3
h3
R12
n
R12
t
N
x
R21
RA1 Mcb
B
A
h
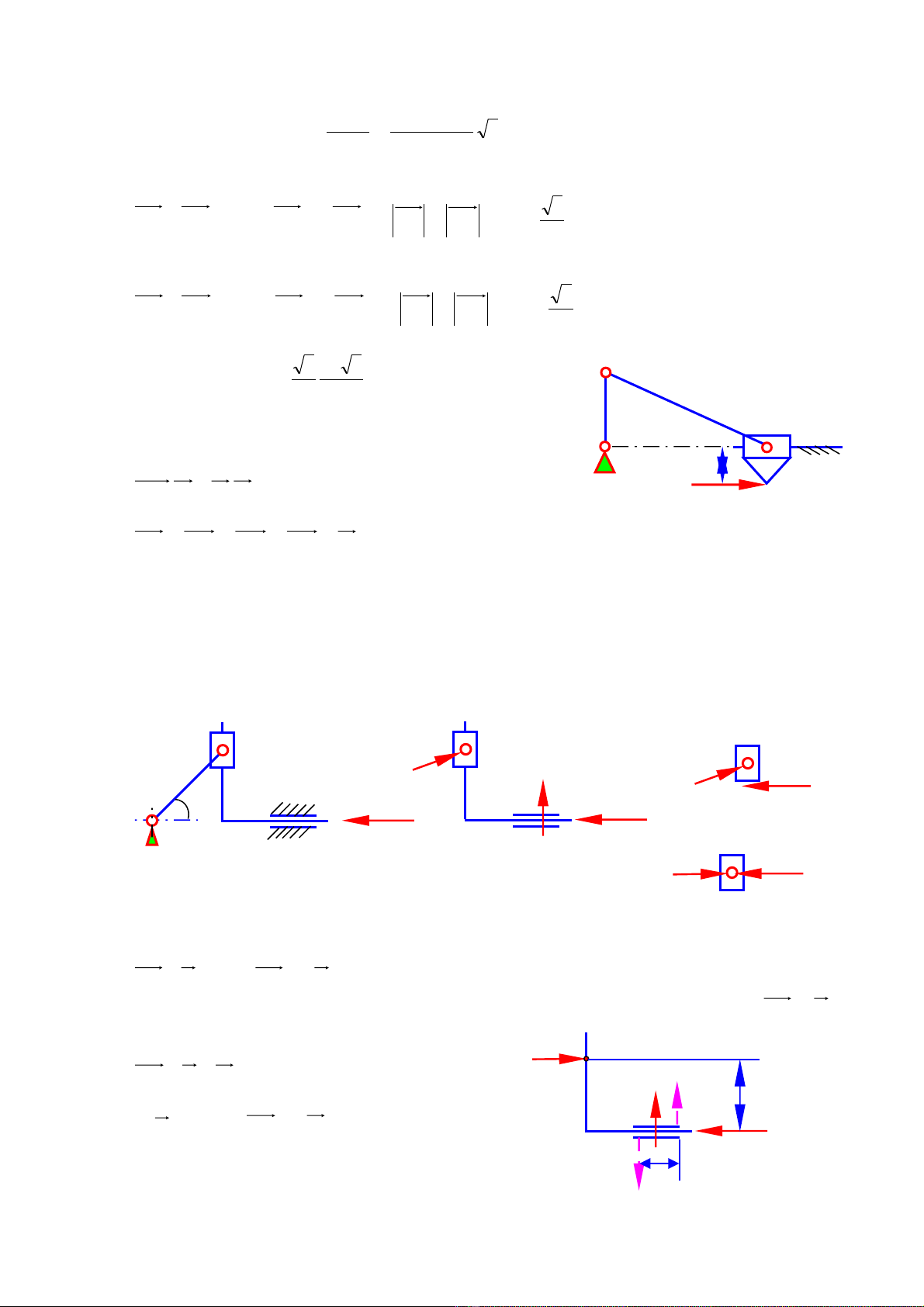
Đ tìm đi m đ t c a áp l c N ta vi t ph ng trình cân b ng mômen c a các l c đ i v i đi m Cể ể ặ ủ ự ế ươ ằ ủ ự ố ớ ể 3:
0.. 33 =− xNhP
m
N
hP
x1,03
1000
058,0.1000
.33 ===
Áp l c N đ t cách tâm C m t kho ng 0,1m.ự ặ ộ ả
Đ tính áp l c t i kh p trong C ta vi t ph ng trình cân b ng l c riêng cho khâu 2:ể ự ạ ớ ế ươ ằ ự
0
3212 =+ RR
3212 RR −=
NRR 3
3
2000
3212 ==
Tính mômen cân b ng đ t t i khâu d n:ằ ặ ạ ẫ
Ph ng trình cân b ng l c t i khâu d n (hình 3.5d):ươ ằ ự ạ ẫ
0
121 =+ A
RR
121 A
RR −=
NRR A3
3
2000
121 ==
Mômen cân b ng có chi u đ c ch n nh hình v 3.5d:ằ ề ượ ọ ư ẽ
NmhRM cb 100
2
31,0
3
3
2000.
21 ===
Chi u Mềcb đã ch n là đúng.ọ
Bây gi chúng ta nghi m l i k t qu trên b ng ph ngờ ệ ạ ế ả ằ ươ
pháp công su t. Gi s khâu AB quay v i v n t c góc ấ ả ử ớ ậ ố
ω1 và ch n chi u Mọ ề cb nh hình v 3.5e.ư ẽ
0.. 331 =+ VPM cb
ω
(3)
ch ng 2 ph n phân tích đ ng h c ta đã bi t: Hình 3.5eỞ ươ ầ ộ ọ ế
3
3221 VVVVV CCBB ====
Chi u c a Mề ủ cb và ω1 là cùng chi u, chi u c a Về ề ủ 3 và P3 là ng c nhau, do v y t ph ng trình (3) taượ ậ ừ ươ
suy ra:
Mcb . ω1 – P3 . V3 = 0 Mcb = P3 . V3 / ω1 = P3 . ω1.lAB / ω1 = P3 . lAB = 1000 . 0,1 = 100Nm.
Chi u Mềcb và giá tr đã ch n là hoàn toàn đúng, phù h p v i ph ng pháp phân tích áp l c.ị ọ ợ ớ ươ ự
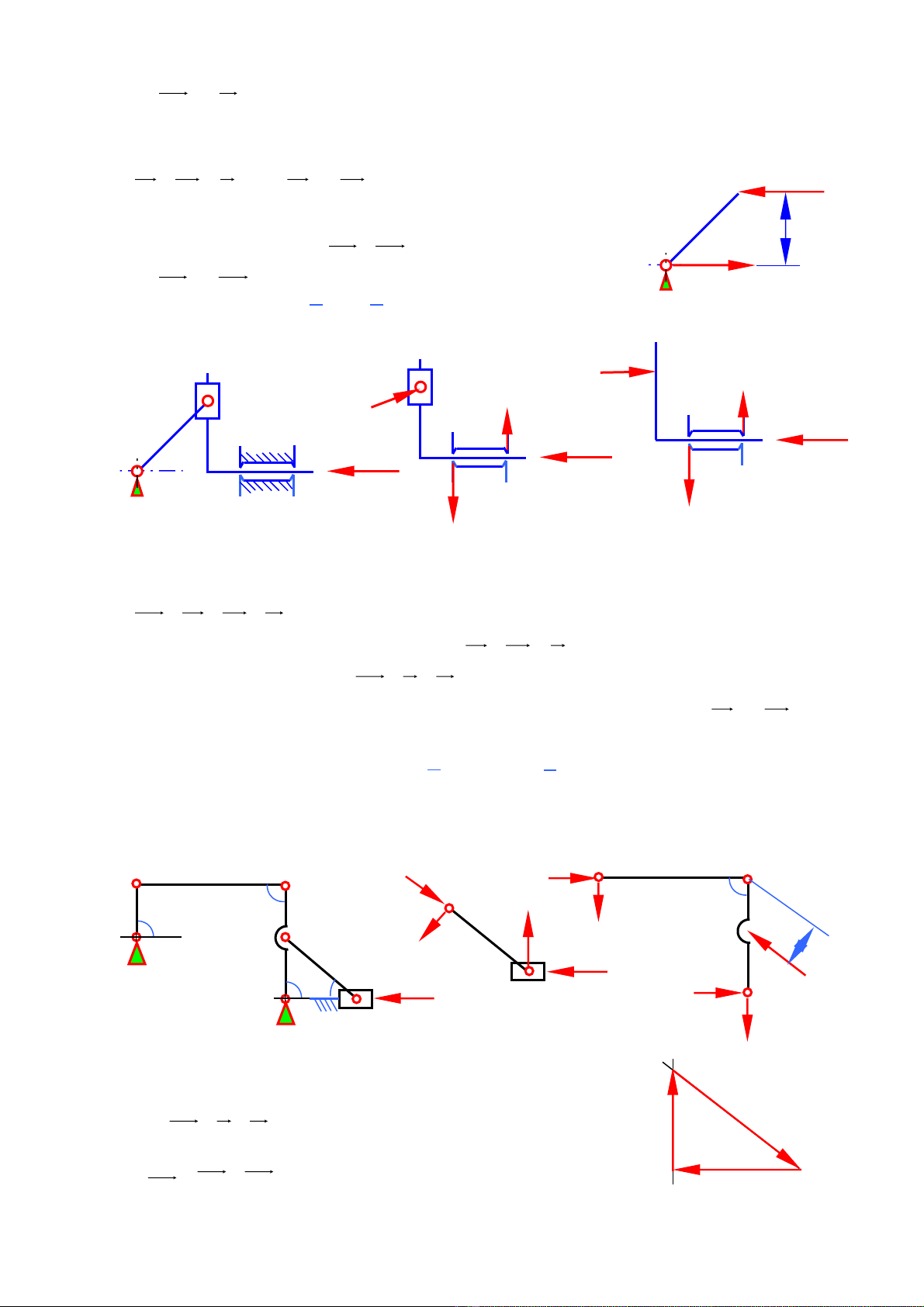
6) Tính nh ng áp l c kh p đ ng và mômen cân b ng trên khâu d n 1 c a c c u tính sin (hìnhữ ự ớ ộ ằ ẫ ủ ơ ấ
3.6a). Cho tr c lướ AB = 0,1m, ϕ1 = 45o, l c c n Pự ả 3 = 1000N. Sau đó gi i bài toán khi rãnh tr tả ượ
ch ti p xúc 2 đi m C’, C’’ v i kho ng cách C’C’’ = 0,2m (hình 3.6b).ỉ ế ở ể ớ ả
Hình 3.6a2
Hình 3.6a Hình 3.6a1
Tách nhóm tĩnh đ nh (hình 3.6a1) Hình 3.6a3ị
Kh p trong là kh p t nh ti n, do v y vi t ph ng trình cân b ng riêng cho t ng khâu. Tách riêng khâuớ ớ ị ế ậ ế ươ ằ ừ
2 (hình 3.6a2)
0
12 =+ NR
NR −=
12
2 l c này song song và ng c chi u nhau.ự ượ ề
L y t ng mô men c a các l c trên khâu 2 đ i v i đi m Bấ ổ ủ ự ố ớ ể 2 (có giá tr b ng 0) d n đ n 2 l c ị ằ ẫ ế ự
NR ,
12
tr c đ i và đ t tai B (hình 3.6a3)ự ố ặ
Xét riêng khâu 3:
0
323 =++ PNR
Chi u ph ng trình này lên ph ng Pế ươ ươ 3 và N:
0=N
và
323 PR −=
Do v y ta th y r ng chi u các l c đã ch n trên hình 3.6a3,ậ ấ ằ ề ự ọ
3.6a4 là h p lý và các l c có giá tr ợ ự ị
R12 = R32 =R23 = P3 = 2000N, N = 0
A
B
C
1
2
3P3
B
C
2
3P3
N
R12
B
R12 R32
B
R12
R32
B
C
3
P3
N
R23
h
N1
N2
x
45o
A
B
C
1
2
3
P3
h3
Do
323 PR −=
và cách nhau m t đo n t o nên m t ng u: Hình 3.6a4ộ ạ ạ ộ ẫ
R23 .h = P3 . h = M
Chính vì th , áp l c t i kh p C ph i phân b đ t o thành m t ng u ch ng l i ng u l c M nói trên đế ự ạ ớ ả ố ể ạ ộ ẫ ố ạ ẫ ự ể
khâu 3 tr ng thái tĩnh đ nh:ở ạ ị
0
21 ==+ NNN
;
21 NN −=
và N1 . x = N2 . x = M
Xác đ nh mômen cân b ng:ị ằ
Xét khâu d n 1 (hình 3.6a5)ẫ
Ph ng trình cân b ng l c: ươ ằ ự
0
121 =+ A
RR
0
121 =−= A
RR
, có giá tr là 1000Nị
Mcb = R21 . h = 1000 . 0,1√2 /2= 50√2 Nm Hình 3.6a5
Ở tr ng h p th hai, xét hình 3.6bườ ợ ứ
Hình 3.6b Hình 3.6b2 Hình 3.6b3
Tác nhóm tĩnh đ nh ra kh i c c u (hình 3.6b). Xét riêng khâu 3 (hình 3.6b3)ị ỏ ơ ấ
Ph ng trình cân b ng l c riêng cho khâu 3:ươ ằ ự
0
32123 =+++ PNNR
Do 2 l c Nự1 và N2 cùng ph ng, cho nên ta có : ươ
NNN =+ 21
Ph ng trình trên đ c vi t l i: ươ ượ ế ạ
0
323 =++ PNR
.
Lúc này cách gi i t ng t nh ph n trên và l y k t qu đã tính, do N = 0 cho nên: ả ươ ự ư ầ ấ ế ả
21 NN −=
.
Nh vây: Nư1 . x = N2 . x = M
Hay :
N1 = N2 = M / x = R23 . h / lC’C’’ = 1000 . 0,1√2 /2 . 0,2 = 250√2 N
7) Tính nh ng áp l c kh p đ ng A, B, C, D và mômen cân b ng trên khâu d n 1 c a c c uữ ự ớ ộ ằ ẫ ủ ơ ấ
máy sàng (hình 3.7a). Cho tr c: lướ AB = lBC/2 = lCD/2 = lDE = 0,1m; ϕ = ϕ23 = ϕ3 = 90o; ϕ4 = 45o.
l c c n Pự ả 3 = 1000N.
Hình 3.7a Hình 3.7b Hình 3.7c
Tính cho nhóm tĩnh đ nh xa khâu d n tr c (nhóm 4,5).ị ở ẫ ướ
Ph ng trình cân b ng l c cho nhóm (4,5) (hình 3.7b):ươ ằ ự
0
334 =++ PNR
(1)
Ph ng trình này t n t i 3 n s , c n ph i kh b t n s :ươ ồ ạ ẩ ố ầ ả ử ớ ẩ ố
τ
3434
34 RRR n+=
Hình 3.7d
A
B
1
MCB
h
R21
RA1
A
B
1
2
3P3
C’ C’’
B 2
3P3
C’ C’’
N1
N2
B
3P3
C’ C’’
N1
N2
R23
FP3
A
BC
D
E
12
34
ϕ1
ϕ23
ϕ3
ϕ4
5
5
E
F
4
R34
n
R34
tN
NR34
P3
P3
BC
D
E
2
3
ϕ23
R12
n
R12
t
RD3
t
RD3
n
R43
h43