Problem_ch2 1
BAØI TẬP CHƯƠNG 2
(ÑS: )
r
2
0
EaR i
r
rR
rR
→
→
<
=>
a
aR
r
rR
rR
ϕ
<
=>
Theá ñieän cuûa tröôøng ñieän tónh phaân boá trong heä caàu :
(bieát a, R = const)
Tìm vectô cöôøng ñoä tröôøng ñieän ?
2.1:
(ÑS: )
6a cos
0
rR
rR
εφ
ρ
<
=>
3
a(3R-2r).r.cos
aR cos
r
rR
rR
φ
ϕφ
<
=>
Theá ñieän cuûa tröôøng ñieän tónh phaân boá
trong heä truï (bieát a, b, R = const) :
Tìm maät ñoä ñieän tích khoái töï do ?
(bieát ε= const)
2.2:
Problem_ch2 2
BAØI TẬP CHƯƠNG 2
(ÑS: Q = -ε0l2(3ad2+ 2bd) = 5.10-9 (C) )
Giöõa 2 ñieän cöïc phaúng hình vuoâng , caïnh l = 0,1 m, caùch nhau d = 5 mm, laø moâi
tröôøng coù ε= ε0toàn taïi theá ñieän : ϕ= ax3 + bx2+ cx vôùi : a = -6,28.108(V/m3), b = -
9,24.105(V/m2), c = -12.102(V/m). Boû qua hieäu öùng meùp, tìm ñieän tích toaøn phaàn
cuûa khoâng gian giöõa 2 ñieän cöïc ?
2.4:
(ÑS: 1 V )
Ei i i
x
yz
yz zx xy
→→ → →
=++
Tìm hieäu theá ñieän giöõa 2 ñieåm A(0, 22,7, 99) vaø B(1, 1, 1) bieát cöôøng ñoä tröôøng
ñieän coù daïng :
2.3:
Baèng 2 caùch :
a) Xaùc ñònh bieåu thöùc cuûa theá ñieän ?
b) Choïn ñöôøng thích hôïp töø A ñeán B cho vieäc tính tích phaân ñöôøng ?
Problem_ch2 3
BAØI TẬP CHƯƠNG 2
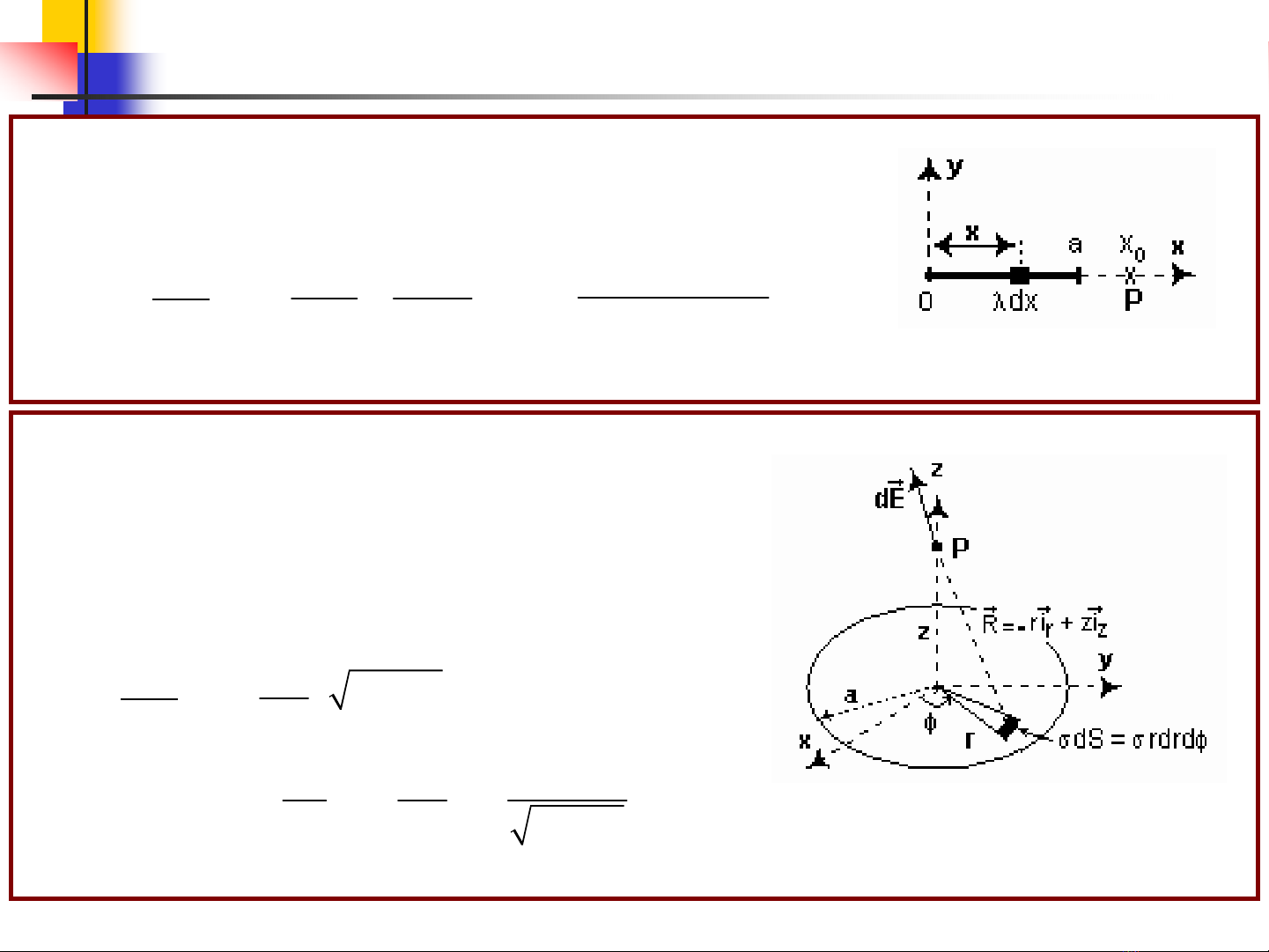
Tìm ϕvaø taïi P(z,0,0) , bieát ñóa troøn tích
ñieän vôùi maät ñoä maët σ? (bieát ε= ε0trong toaøn
khoâng gian)
E
→
2.6:
(ÑS:
)
22
0
2azz
σ
ϕε

=+−

22
0
z
Ei 1 i
2
zz
d
dz az
ϕσ
ε
→→ →

=− = −

+

2.5:Tìm ϕvaø taïi P(x0,0,0) do ñoaïn daây chieàu daøi a, mang
ñieän vôùi maät ñoä daøi λtaïo ra ? (bieát ε= ε0)
E
→
(ÑS: )
0
00
ln
4
x
xa
λ
ϕπε
=
−
00 0
;E i
4()
x
a
xx a
πε
→→
=−
Problem_ch2 4
BAØI TẬP CHƯƠNG 2
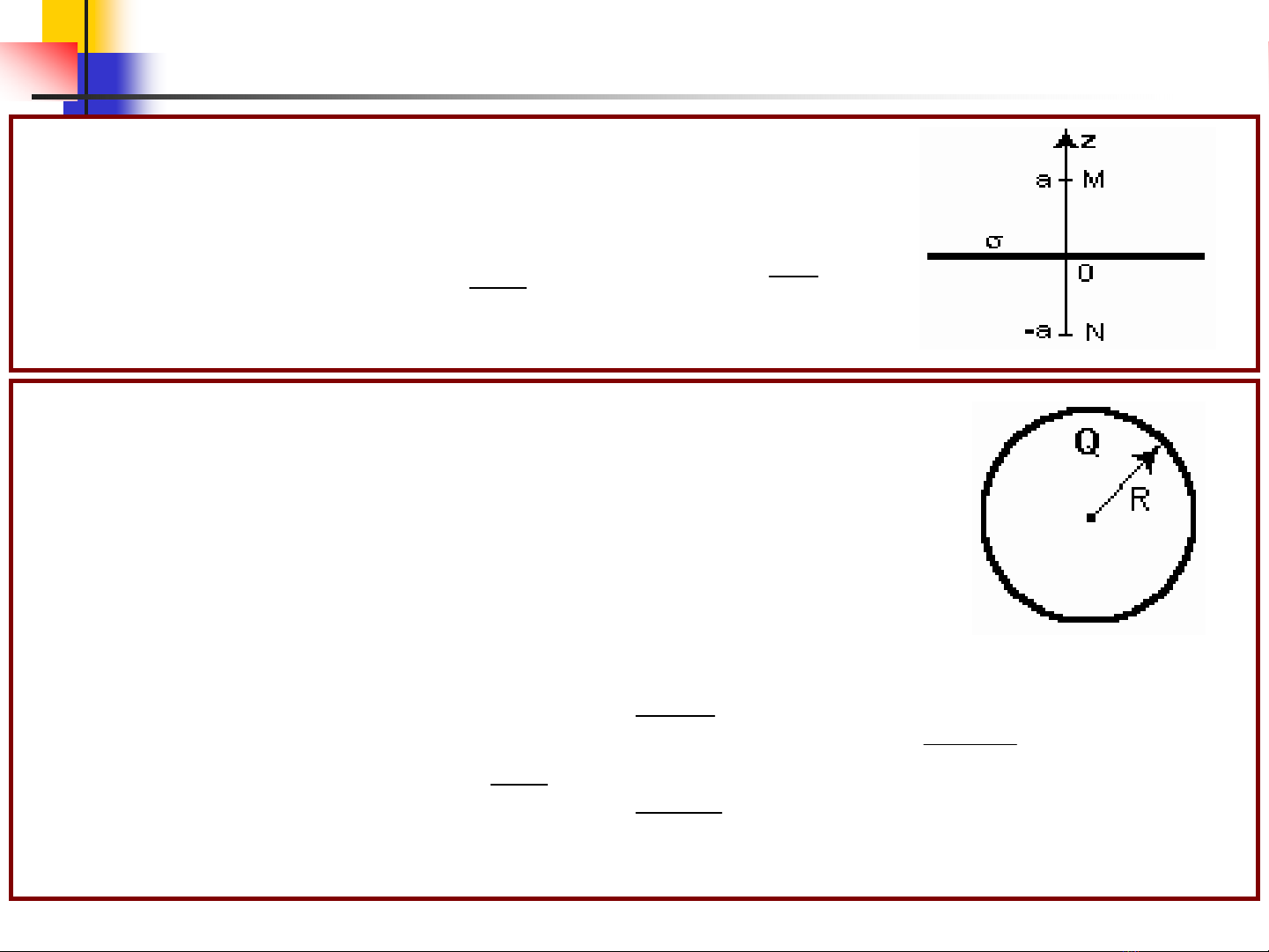
2.7: Maët phaúng roäng voâ haïn tích ñieän vôùi maät ñoä maët σ=
const , bieát ε= ε0, tìm UMO vaø UNO ?
(ÑS: )
0
2
MO NO
a
UU
σ
ε
==−
Maët caàu daãn , baùn kính R, mang ñieän tích Q. Bieát ε= ε0
trong toaøn khoâng gian, tìm vectô cöôøng ñoä tröôøng ñieän vaø
theá ñieän trong vaø ngoaøi voû caàu baèng hai caùch :
a) Duøng luaät Gauss ?
b) Duøng phöông trình Poisson-Laplace ? (Löu yù xaùc ñònh
ñuû caùc phöông trình ñieàu kieän bieân , xem lyù thuyeát 2.4)
2.8:
(ÑS: )
0
0
4
4
QrR
r
QrR
R
πε
ϕ
πε
>
=
<
2
0
i
4
;E
0
r
QrR
r
rR
πε
→
→>
=
<
Problem_ch2 5
BAØI TẬP CHƯƠNG 2
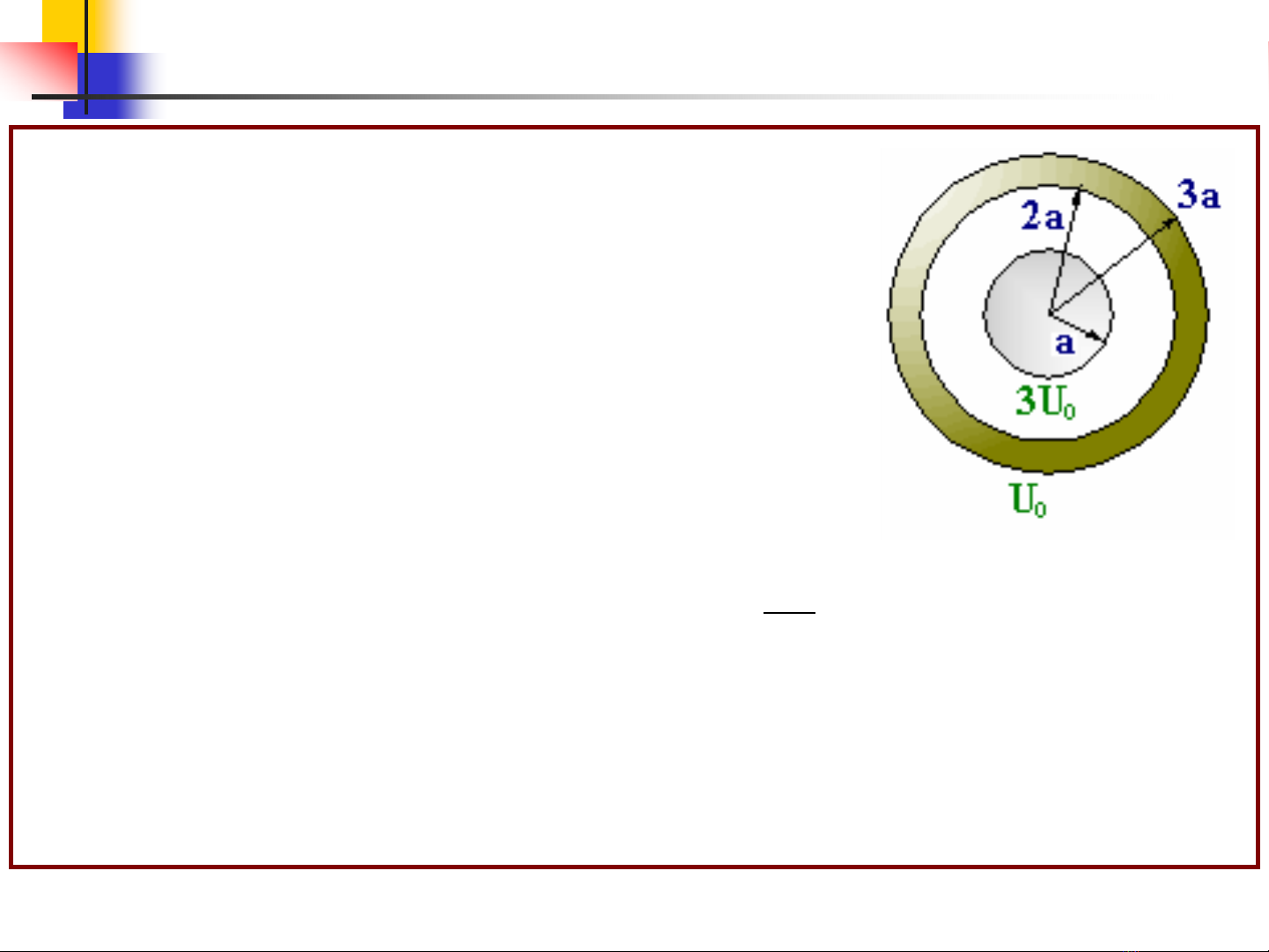
Quaû caàu daãn, bkính a, theá ñieän 3U0, ñaët ñoàng
taâm vôùi voû caàu daãn , bkính 2a vaø 3a, theá ñieän U0.
Bieát ε= ε0trong toaøn khoâng gian. Choïn ϕ∞= 0,
xaùc ñònh theá ñieän caùc mieàn :
a) Mieàn r < a :
b) Mieàn a < r < 2a :
c) Mieàn 2a < r < 3a :
d) Mieàn r > 3a :
2.9:
(ÑS: a) 3U0
b) U0(4a/r – 1)
c) U0
d) 3U0/r )