
BK
TP.HCM
2011
dce
Chương 3
Biến đổi Z
©2011, TS. Đinh Đức Anh Vũ

2011
dce
2
DSP – Biến đổi Z © 2 0 1 1 , Đinh Đức Anh Vũ
• Biến đổi Z
–BĐ thuận
–BĐ ngược
•Các tính chất của BĐ Z
•BĐ Z hữu tỉ
–Điểm không (Zero) – Điểm cực (Pole)
–Pole và t/h nhân quảtrong miền thời gian
–Mô tảh/t LTI bằng hàm hệthống
• Biến đổi Z ngược
–Phương pháp tích phân
–Phương pháp khai triển thành chuỗi lũy thừa
–Phương pháp phân rã thành các hữu tỉ
• Biến đổi Z một phía (Z+)
–Tính chất
–Giải PTSP bằng BĐ Z+
•Phân tích hệLTI
–Đáp ứng của hệ
–Đáp ứng tức thời, quá độ
–Tính ổn định và nhân quả
Nội dung
2011
dce
3
DSP – Biến đổi Z © 2 0 1 1 , Đinh Đức Anh Vũ
• Tổng quát
– Một cách biểu diễn t/h khác vềmặt toán học
– Biến đổi t/h từmiền thời gian sang miền Z
– Dễkhảo sát t/h và h/t trong nhiều trường hợp (dựa vào các t/c của BĐZ)
•Định nghĩa
–Công thức
–Quan hệ
– Ký hiệu X(z) ≡Z{x(n)}
– Biến zĐiểm thuộc mặt phẳng z
z = a + jb hay z = rejδ
– Miền hội tụ(ROC) {z │|X(z)| < ∞}
Chỉquan tâm X(z) tại những điểm z thuộc ROC
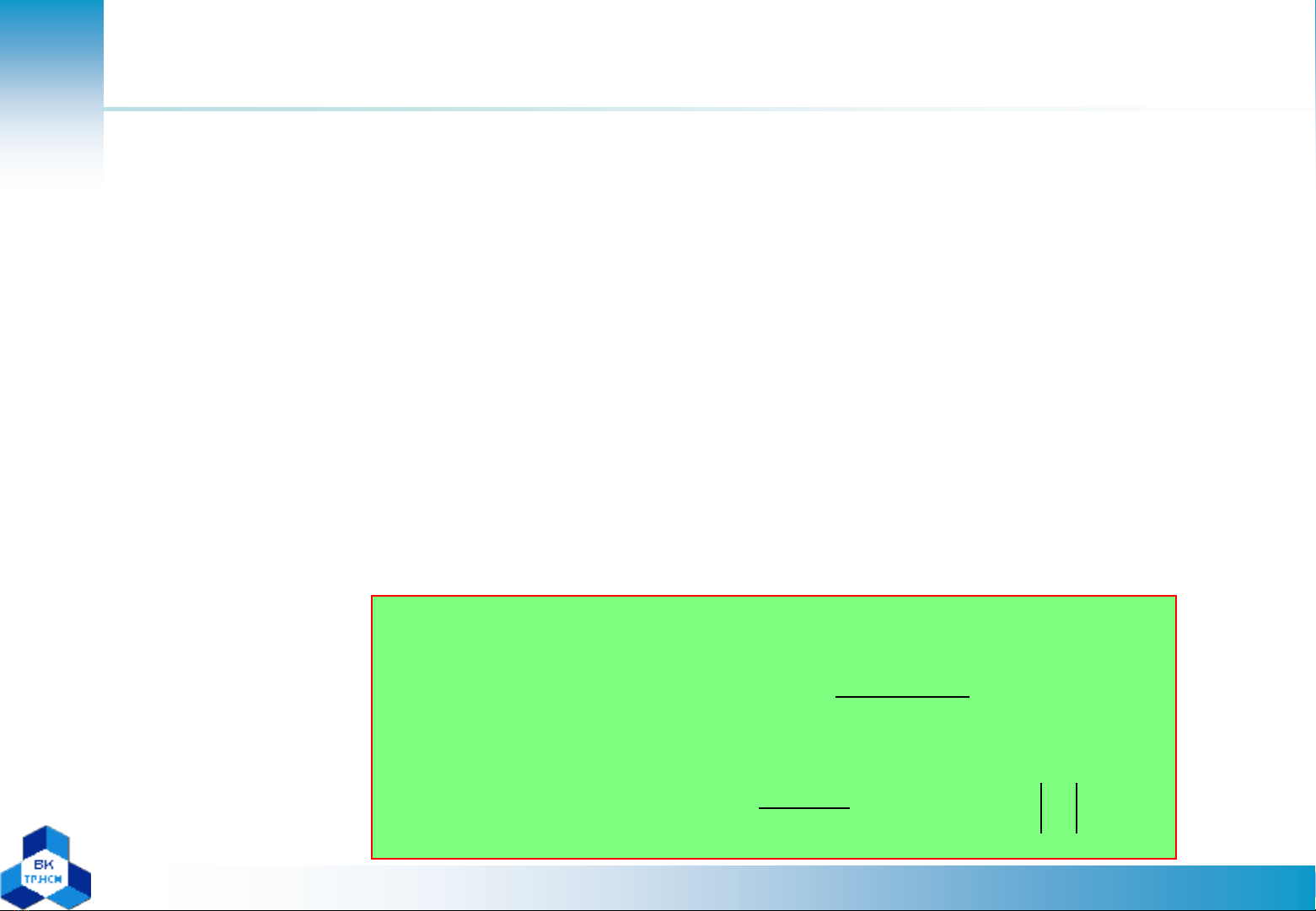
Biến đổi Z
() ()
n
n
Xz xnz
+∞ −
=−∞
=∑
() ()
z
xn Xz← →
2011
dce
4
DSP – Biến đổi Z © 2 0 1 1 , Đinh Đức Anh Vũ
– x1(n) = δ(n)
X1(z) = 1
ROC = mặt phẳng z (mpz)
– x2(n) = {8 10 1^ 9 7 2}
X2(z) = 8z2+ 10z + 1 + 9z–1 + 7z–2 + 2z–3
ROC = mpz \ (∞, 0)
– x3(n) = δ(n –k)
X3(z) = z–k
ROC = mpz \{0 nếu k>0, ∞ nếu k<0)
• Nhắc lại
Ví dụvề BĐZ
1
1
1
1
1
1
1
11
1
32
1
32
<
−
=++++
≠
−
−=+
=++++ +
A
A
AAA
A
A
A
An
AAAA n
n

2011
dce
5
DSP – Biến đổi Z © 2 0 1 1 , Đinh Đức Anh Vũ
BĐZ của t/h nhân quảvà không nhân quả
•T/h nhân quảx(n) = anu(n)
•T/h phản nhân quảx(n) = –anu(–n–1)
• Ý nghĩa
–T/h RRTG x(n) được xác định duy nhất bởi biểu thức BĐ Z và ROC của
nó
– ROC của t/h nhân quảlà phần ngoài của vòng tròn bán kính r2, trong khi
ROC của t/h phản nhân quảlà phần trong của vòng tròn bán kính r1
azROC
az
zXazeiazKhi
azznxzX
n
n
n
n
>⇒
−
=><
==
−
−
+∞
=
−
+∞
−∞=
−∑∑
:
1
1
)(),..(1
)()()(
1
1
0
1
azROC
azza
za
zXazeizaKhi
zazaznxzX
l
l
n
nn
n
n
<⇒
−
=
−
−=<<
−=−==
−−
−
−
∞
=
−
−
−∞=
−
+∞
−∞=
−∑∑∑
:
1
1
1
)(),..(1
)()()()(
11
1
1
1
1
1

![Bài giảng Toán cao cấp (A2) - TS. Lê Bá Long, ThS. Đỗ Phi Nga [Chuẩn Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250428/vihizuzen/135x160/7081745803521.jpg)




![Bài giảng Toán cao cấp 2: Bài 3 - Nguyễn Phương [CHUẨN SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250313/myhouse05/135x160/2874133_9851.jpg)
![Bài giảng Toán cao cấp 2: Bài 2 - Nguyễn Phương [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250313/myhouse05/135x160/2874132_4256.jpg)


















