ĐỀ ÔN THI TUYỂN SINH LỚP 10 THPT
ĐỀ SỐ 7
Câu 1: a) Tìm điều kiện của x biểu thức sau có nghĩa: A =
x - 1 + 3 - x
b) Tính:
1 1
3 5 5 1
Câu 2: Giải phương trình và bất phương trình sau:
a) ( x – 3 )2 = 4
b)
x - 1 1
<
2x + 1 2
Câu 3: Cho phương trình ẩn x: x2 – 2mx - 1 = 0 (1)
a) Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt x1 và x2.
b) Tìm các giá trị của m để: x12 + x22 – x1x2 = 7.
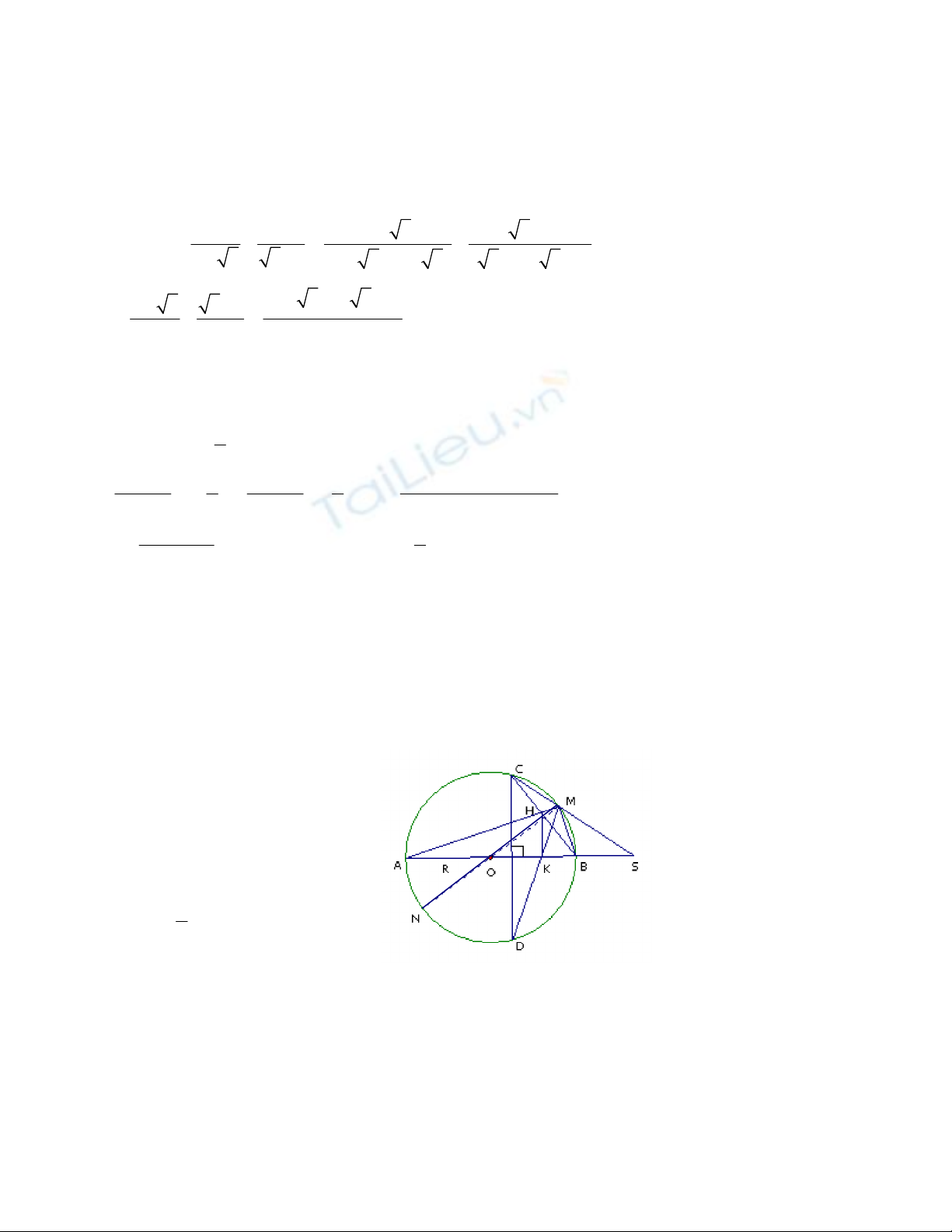
Câu 4: Cho đường tròn (O;R) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD
không đi qua tâm O). Trên tia đối của tia BA lấy điểm S; SC cắt (O; R) tại điểm thứ hai là M.
a) Chứng minh ∆SMA đồng dạng với ∆SBC.
b) Gọi H là giao điểm của MA và BC; K là giao điểm của MD và AB. Chứng minh
BMHK là tứ giác nội tiếp và HK // CD.
c) Chứng minh: OK.OS = R2.
Câu 5: Giải hệ phương trình: 3
3
x + 1 = 2y
y + 1 = 2x
.
ĐỀ SỐ 7
Câu 1: a) Biểu thức A có nghĩa - 1 0
3 - 0
xx
x.
b)
1 1 3 5 5 1
3 5 5 1
3 5 3 5 5 1 5 1
=
3 5 5 1
3 5 5 1
1
9 5 5 1 4
.
Câu 2: a) ( x – 3 )2 = 4
x – 3 = ± 2
5
1
x
x.
Vậy phương trình có 2 nghiệm x = 5; x = 1
b) Đk:
1
x
2
.
- 1 1 - 1 1 (2 - 2) - (2 1)
- 0 0
2 1 2 2 1 2 2(2 1)
x x x x
x x x
3 1
0 2x + 1 > 0 x > -
2 2x + 1 2
.
Câu 3: a) Ta có ∆/ = m2 + 1 > 0, m R. Do đó phương trình (1) luôn có hai nghiệm phân biệt.
b) Theo định lí Vi-ét thì: x1 + x2 = 2m và x1.x2 = - 1.
Ta có: x12 + x22 – x1x2 = 7
(x1 + x2)2 – 3x1.x2 = 7
4m2 + 3 = 7
m2 = 1
m = ± 1.
Câu 4:
a) ∆SBC và ∆SMA có:
BSC MSA
,
SCB SAM
(góc nội tiếp cùng chắn
MB
).
SBC SMA
~ .
b) Vì AB CD nên
AC AD
.
Suy ra
MHB MKB
(vì cùng
bằng
1
(sdAD sdMB)
2
t
ứ
giác BMHK nội tiếp được đư
ờng
tròn
0
HMB HKB 180
(1).
Lại có:
0
HMB AMB 90
(2)
(góc nội tiếp chắn nửa đường tròn).
Từ (1) và (2) suy ra
0
HKB 90
, do đó HK // CD (cùng vuông góc với AB).
c) Vẽ đường kính MN, suy ra
MB AN
.
Ta có:
1
OSM ASC
2
(sđ
AC
- sđ
BM
);
1
OMK NMD
2
sđ
ND
=
1
2
(sđ
AD
- sđ
AN
);
mà
AC AD
và
MB AN
nên suy ra
OSM OMK
OSM OMK
~ (g.g)
2 2
OS OM
OK.OS = OM R
OM OK
.
Câu 5: Giải hệ phương trình: 3
3
1 2 (1)
1 2 (2)
x y
y x
Lấy pt (1) trừ pt (2) ta được: x3 – y3 = 2(y – x)
(x – y)(x2 – xy + y2 + 2) = 0
x – y = 0
x = y.
( do x2 – xy + y2 + 2 =
22
y 3y
x - 2 0
2 4
)
Với x = y ta có phương trình: x3 – 2x + 1 = 0
(x – 1)(x2 + x – 1) = 0
-1+ 5 -1- 5
x = 1; x = ; x=
2 2
.
Vậy hệ đã cho có 3 nghiệm là:
1 5 1 5 1 5 1 5
1;1 , ; , ;
2 2 2 2
.