PHÒNG GD&ĐT HUY N Č M’GARỆ Ư
TR NG THCS NGÔ QUY N ƯỜ Ề
MA TR N Đ THI HSG C P TR NGẬ Ề Ấ ƯỜ
NĂM H C: 2017 - 2018Ọ
Môn: Toán 9
Th i gianờ: 120 phút (không k th i gian giao để ờ ề)
M c đứ ộ
Ch đủ ề
Nhậ
n
bi tế
Thông
hi uể
V n d ngậ ụ
C p đ th pấ ộ ấ
V n d ngậ ụ
C p đ caoấ ộ T ngổ
1. c c a Ướ ủ
m t s ộ ố
nguyên
V n d ng c c a ậ ụ ướ ủ
m t s nguyên đ ộ ố ể
tìm các s nguyên ố
ch a bi t trong bi uư ế ể
th cứ
1(bài 1b)
2,5
12,5%
1
2,5
12,5%
2. Nghi m ệ
c a đa th củ ứ
V n d ng cách tìm ậ ụ
nghi m c a đa th c ệ ủ ứ
đ ch ng minh đa ể ứ
th c không có ứ
nghi mệ
1(bài 2a)
1,5
7,5%
1
1,5
7,5%
3. Phân tích
đa th c ứ
thành nhân
tử
V n d ng các ph ngậ ụ ươ
pháp phân tích thành
nhân t đ phân tích ử ể
đa th c thành nhân tứ ử
Câu số
S đi m ố ể
T l %ỉ ệ
1(Bài1a)
2,5
12,5%
1
2,5
12,5%
4. Các phép
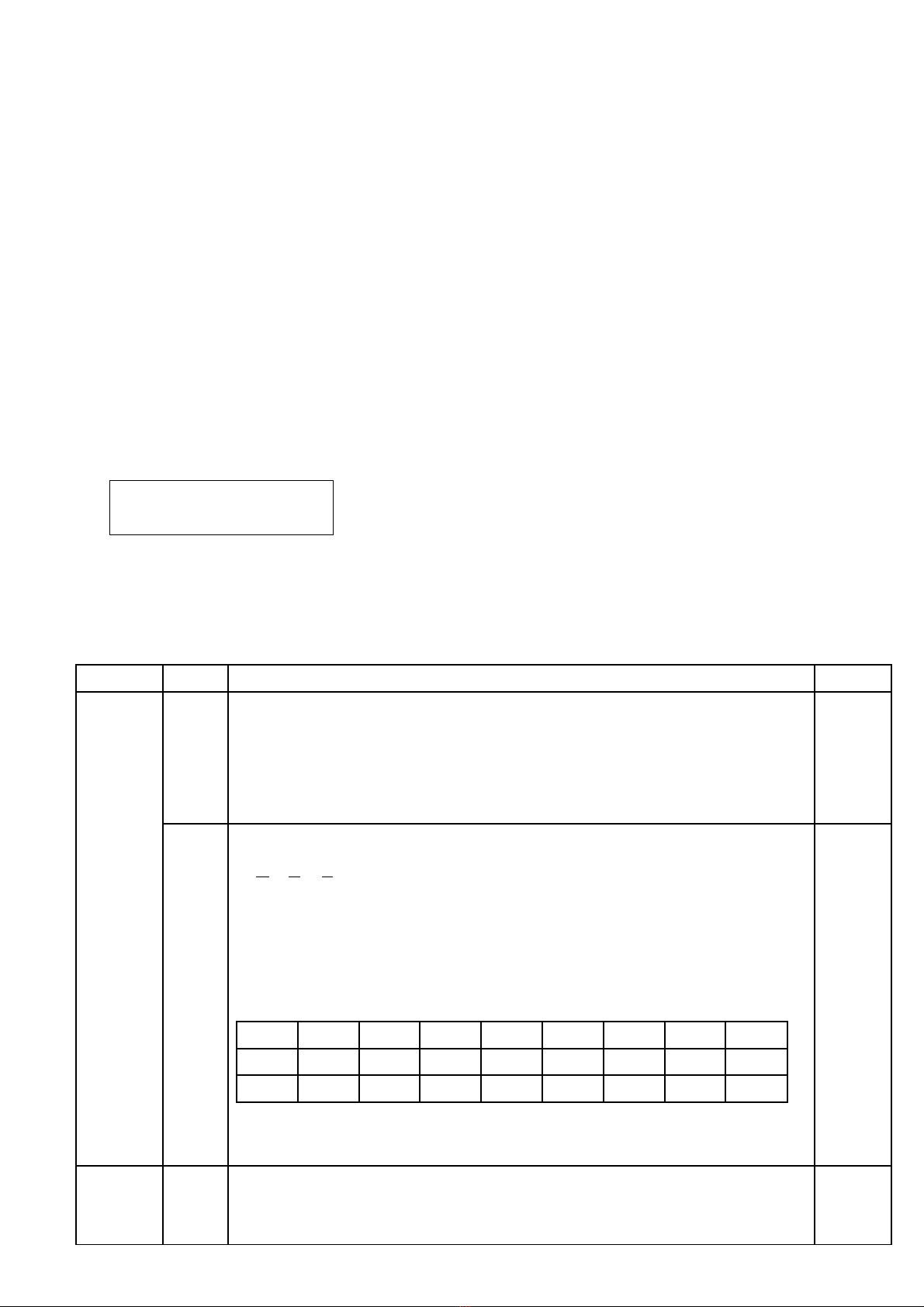
bi n đi căn ế ổ
th c b c haiứ ậ
V n d ng ậ ụ các phép
bi n đi căn th cế ổ ứ
b c hai ậ
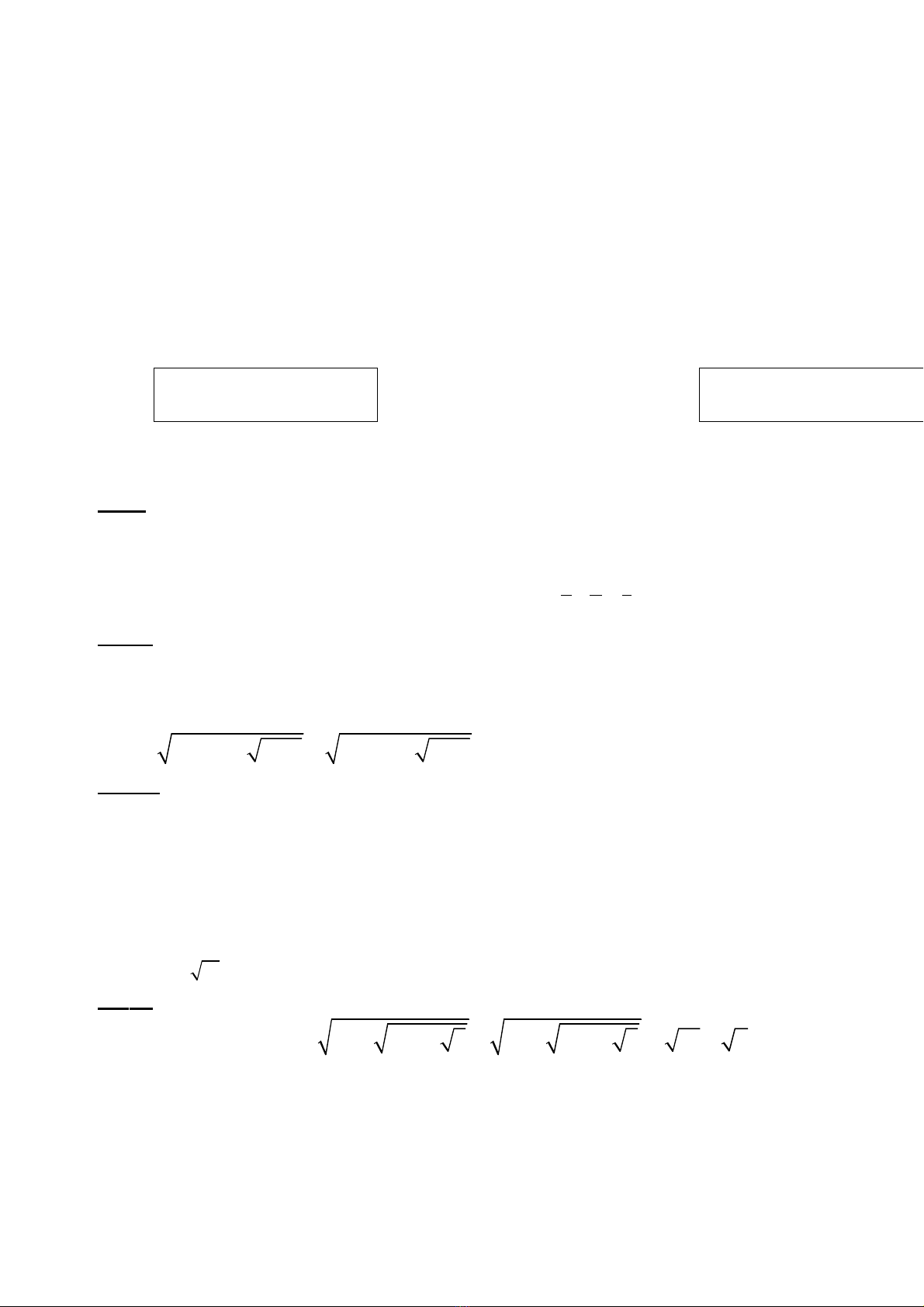
2
A A=
để
gi i ph ng trình,ả ươ
Ch ng minh đngứ ẳ
th c ứ
Câu số
S đi m ố ể
T l %ỉ ệ
2(bài 2b. Bàì 5)
4,5
22,5%
2
4,5
22,5%
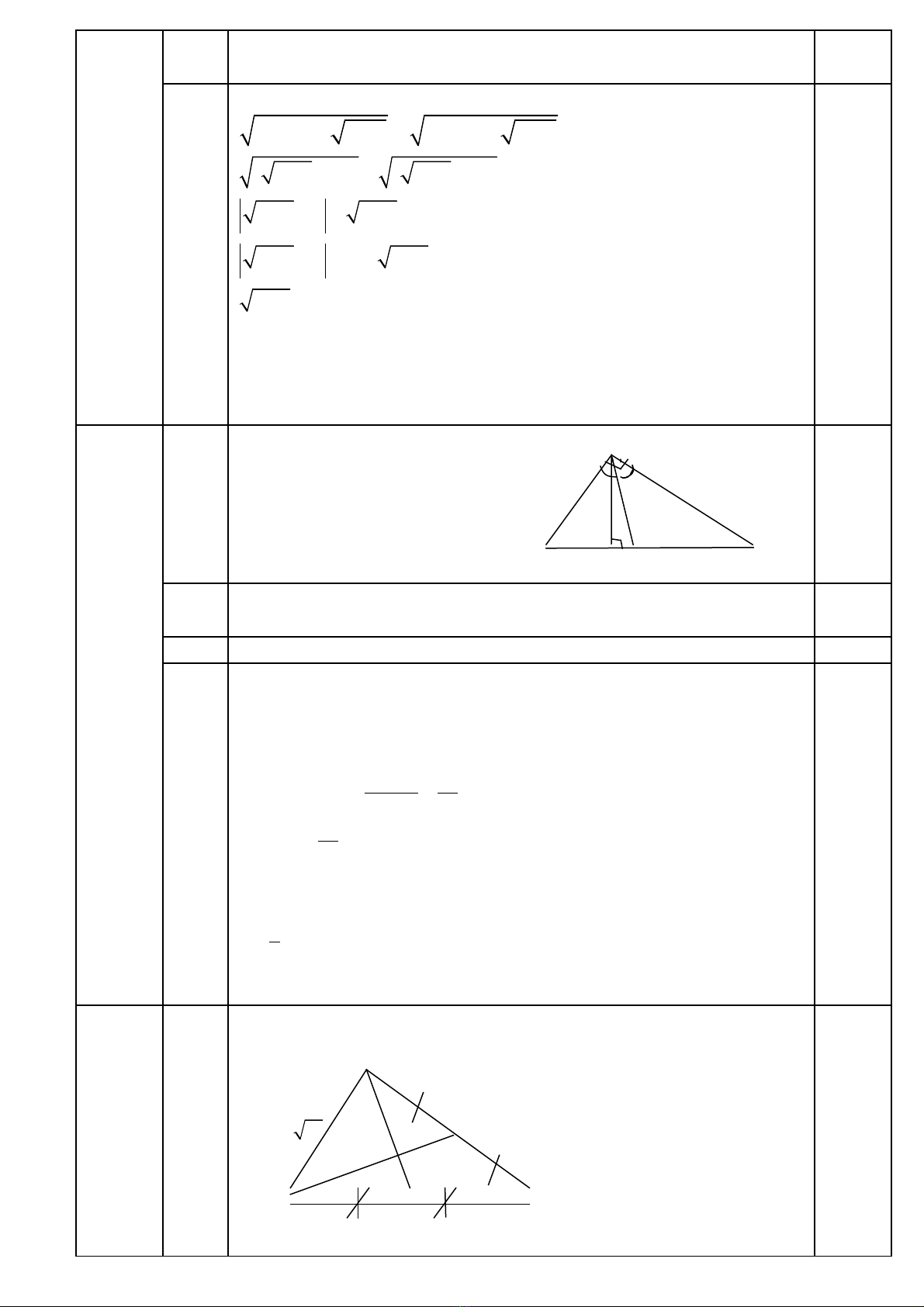
5. tính ch t ấ
đng trungườ
V n d ng, ậ ụ tính ch tấ
đng trung tuy n ườ ế
Đ CHÍNH TH CỀ Ứ
tuy nếđ ch ng minh, tínhể ứ
đ dài đo n th ngộ ạ ẳ
1(Bài 4)
2
10%
1
2
10%
6. Tam giác
đng d ngồ ạ
V n d ng tr ng ậ ụ ườ
h p đng d ng c a ợ ồ ạ ủ
hai tam giác, tính
ch t đng phân giácấ ườ
đ ch ng minh hai ể ứ
tam giác đng ồ
d ng,ch ng minh h ạ ứ ệ
th c g a các đo n ứ ữ ạ
th ngẳ
Câu số
S đi m ố ể
T l %ỉ ệ
2(bài 3 b,c)
4
20%
2
4
30%
7.H th c ệ ứ
l ng trong ượ
tam giác
V n d ng h th c ậ ụ ệ ứ
l ng trong tam giác ượ
đ tính đ dài các ể ộ
đô n th ngạ ẳ
Câu số
S đi m ố ể
T l %ỉ ệ
1(bài 3a)+gt,kt,v ẽ
hình
3
15%
1
3
15%
T ng:ổ
S câuố
S đi m ố ể
T l %ỉ ệ
5
11
55%
4
9
45%
9
20
100%
PHÒNG GD&ĐT HUY N Č M’GARỆ Ư
TR NG THCS NGÔ QUY N ƯỜ Ề
K THI CH N H C SINH GI I C PỲ Ọ Ọ Ỏ Ấ
TR NG ƯỜ
NĂM H C 2017-2018Ọ
Khóa thi: Ngày 20/ 10/ 2017
MÔN: TOÁN 9
Th i gian:ờ 120 phút (không k th i gian giao để ờ ề)
Bài 1:(5 đi m ể).
a) Phân tích đa th c sau thành nhân tứ ử :
x5 + x4 + 1
b) Tìm các c p các s nguyên x và y đ cho ặ ố ể
1 3
8 8
x
y
− =
Bài 2: (4 đi mể)
a, Ch ng minh đa th c sau không có nghi m:ứ ứ ệ
4x2 + 4x + 5
b, Gi i ph ng trình ả ươ
3 4 1 8 6 1 5x x x x
+ − − + + + − =
Câu 3: (7 đi m) Cho tam giác ABCvuông t i A, đng cao AH (Hể ạ ườ
BC).
Bi t AB = 33cm , BC = 65cm.ế
a) Tính đng cao HC.ườ
b) Ch ng minh tam giác AHB đng d ng tam giác CHA.ứ ồ ạ
c) G i AE là phân giác c a góc A( Eọ ủ
BC). Tính di n tích Tam giác AEB.ệ
Bài 4: (2 đi mể)
Cho tam giác ABC vuông t i A các đng trung tuy n AD và BE vuông góc t i G ạ ườ ế ạ
bi t AB =ế
18
. Tính c nh huy n BCạ ề
Bài 5: (2 đi m). ể
Ch ng minh A = ứ
8 2 10 2 5 8 2 10 2 5 10 2
+ + + − + = +
-----------------------------H T---------------------------Ế
Đ CHÍNH TH CỀ Ứ Đ CHÍNH TH CỀ Ứ
PHÒNG GD&ĐT HUY N Č M’GARỆ Ư
TR NG THCS NGÔ QUY N ƯỜ Ề
H NG D N CH M ƯỚ Ẫ Ấ
K THI CH N H C SINH GI I C PỲ Ọ Ọ Ỏ Ấ
TR NG ƯỜ
NĂM H C 2017-2018Ọ
Khóa thi: Ngày 20/ 10/ 2017
MÔN: TOÁN 9
Th i gian:ờ 120 phút (không k th i gian giao để ờ ề)
Bài Câu N i dungộĐi mể
Bài 1
5 đi m ểa x5 + x4 + 1 =
= x5 + x4 + x3 - x3 + x2 - x2 + x - x +1
= (x5+x4+x3) -(x3+x2 +x) +(x2 +x+1)
= x3(x2 +x+1) - x(x2+x+1) + (x2 +x+ 1)
= (x2 + x +1) ( x3 - x +1)
1
0,5
0,5
0,5
bĐi u ki n xề ệ
0
2 3
5 5
y
x
− =
xy – 10 = 3x
xy – 3x = 10
x(y – 3) = 10 Suy ra x, y – 3là (10)Ư
(10) = Ư
Xét b ng ả
x -1 1 - 2 2 - 5 5 - 10 10
y-3 -10 10 - 5 5 - 2 2 - 1 1
y -7 13 - 2 8 1 5 2 4
V y có 8 c p s nguyên (x,y)th a mãn: (- 1;- 5); (1;13); ậ ặ ố ỏ
(- 2;-2); (2; 8); (-5; 1); (5; 5); (10; 2); (10; 4)
0,25
0,25
0,5
0,25
1,0
0,25
Bài 2
4 đi mểa 4x2 + 4x + 5 = (2x)2 + 2.2x + 1 + 4
(2x +1)2 + 4
Vì (2x +1)2
0 v i m i xớ ọ
0,5
0,25
0,25
Đ CHÍNH TH CỀ Ứ
Nên (2x +1)2 + 4 > 0 v i m i xớ ọ
Do đó f(x) không có nghi mệ0,25
0,25
bĐKXĐ ta đc x ượ
1
3 4 1 8 6 1 5x x x x
+ − − + + + − =
2 2
( 1 2) ( 1 3) 5
1 2 1 3 5
1 2 2 1
1 2 0
5
x x
x x
x x
x
x
− − + − + =
− − + − + =
− − = − −
− −
K t h p v i ĐKXĐ ta đc 1 ế ợ ớ ượ
x
5
0,25
0,5
0,5
0,5
0,5
0,25
Bài 3
7 đi mểV hình ,ghi GT và KL đúng Aẽ
B H E C
1
a Tính đc AC = 56cmượ
Tính đc HC ượ ≈ 48,246cm
1
1
b Ch ng minh đc tam giác AHB đng d ng v i tam giác CHAứ ượ ồ ạ ớ 1,5
CÁp d ng đc tính ch t đng phân giác trong c a tam giác ụ ượ ấ ườ ủ
tính đc ượ
=
Theo tính ch t c a dãy t s b ng nhau suy ra:ấ ủ ỉ ố ằ
= = = =
65 65
33 56 89
=
+
EB =
65
89
. 33
24,101 (cm)
Ta có: AH.BC=AB.AC
AH=(AB.AC):BC
=(33.56):65
28,431(cm)
S =
2
1
EB. AH
.24,101.28,431
342,608 (cm2 )
0,5
0,5
0,5
0,5
0,5
Bài 4
2 đi mể V hình ,ghi GT và KL đúng ẽ
A
18
E
G
B D C
Áp d ng h th c bụ ệ ứ 2 = ab/ trong Δ vuôngABE ta có: AB2 =
0,5