
TR NG THPT NGUY N TRÃIƯỜ Ễ
------------
Đ THI KI M TRA H C KỲ 1Ề Ể Ọ
MÔN TOÁN - L P 11Ớ
NĂM H C 2012 - 2013Ọ
I. Ph n chung (8 đi m)ầ ể
Câu 1: (3 đi m)ể
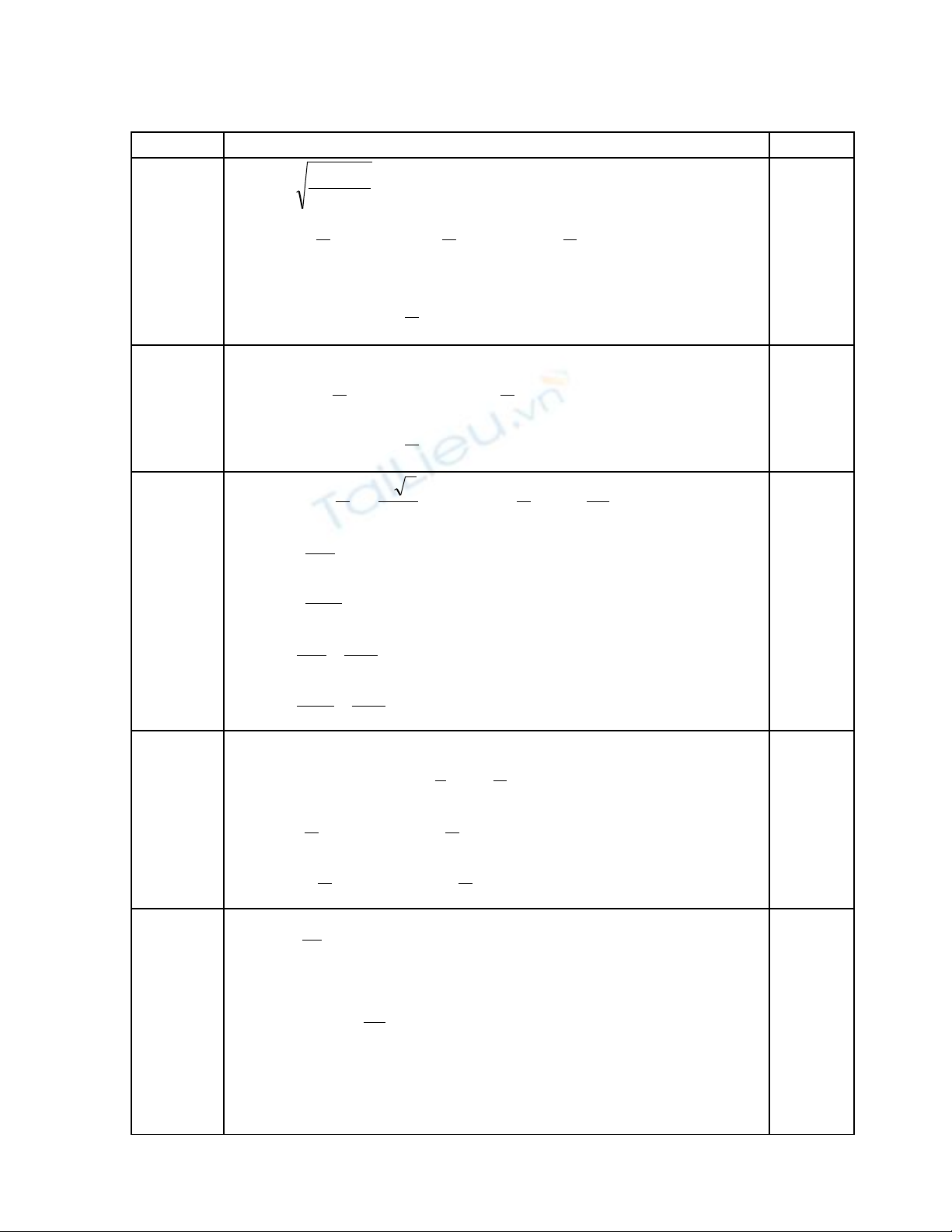
1. Tìm TXĐ c a hàm s (1 đi m)ủ ố ể
a.
1cos
tan 2
+
=x
x
y
b.
( )
3tan += xy
.
2. Gi i ph ng trình (2 đi m)ả ươ ể
a.
2
2
6
3cos −
=
−
π
x
b.
22coscos2 2=+ xx
Câu 2: (2 đi m)ể
1. (1 đi m)Tìm h s c a s h ng ch a ể ệ ố ủ ố ạ ứ x5 trong khai tri n: ể
8
2
1
2
−x
x
2. (1 đi m) Cho m t h p đ ng 12 viên bi, trong đó có 7 viên bi màu đ , 5ể ộ ộ ự ỏ
viên bi màu xanh. Tính xác su t trong hai tr ng h p sau:ấ ườ ợ
a. L y đ c 3 viên bi màu xanh.ấ ượ
b. L y đ c ít nh t 2 viên bi màu xanh.ấ ượ ấ
Câu 3: (1 đi m)ể
Trong m t ph ng ặ ẳ Oxy cho A(1;2) và đ ng th ng: ườ ẳ
032 =+− yx
. Hãy tìm
nh c a ả ủ A và d qua phép t nh ti n theo véc t ị ế ơ
( )
4;1=u
.
Câu 4: (2 đi m)ể
Cho hình t di n ABCD. G i M, N l n l t là các đi m trên các c nh BC,ứ ệ ọ ầ ượ ể ạ
CD sao cho BM=MC và CN=
1
4
CD. G i G là tr ng tâm tam giác ABC.ọ ọ
a. Tìm giao tuy n c a hai m t ph ng (ABD) và (AMN).ế ủ ặ ẳ
b. Tìm giao đi m c a đ ng th ng NG v i m t ph ng (ABD).ể ủ ườ ẳ ớ ặ ẳ
II. Ph n t ch n (2 đi m)ầ ự ọ ể
H c sinh ch n m t trong hai ph n sau:ọ ọ ộ ầ
Ph n 1: Theo ch ng trình chu n.ầ ươ ẩ
Câu 5a: (1 đi m) Tìm s h ng đ u và công sai c a c p s c ng:ể ố ạ ầ ủ ấ ố ộ
=+−
=+
22
15
742
93
uuu
uu
Câu 6a: (1 đi m) Có 10 c p v ch ng đi d ti c. Tính s cách ch n 1 ng iể ặ ợ ồ ự ệ ố ọ ườ
đàn ông và 1 ng i đàn bà trong b a ti c đ phát bi u ý ki n đ phát bi u ý ki nườ ữ ệ ể ể ế ể ể ế
sao cho hai ng i đó là v ch ng?ườ ợ ồ
Ph n 2:Theo ch ng trình nâng caoầ ươ
Câu 5b: (1 đi m) Tìm GTLN, GTNN c a hàm s sau:ể ủ ố
24cos44sin3 +−= xxy
Câu 6b: (1 đi m) M t đ n c nh sát khu v c có 9 ng i. Trong ngày c n c 3ể ộ ồ ả ự ườ ầ ử
ng i làm nhi m v đ a đi m A, 2 ng i đ a đi m B, còn 4 ng i th ngườ ệ ụ ở ị ể ườ ở ị ể ườ ườ
tr c t i đ n. H i có bao nhiêu cách phân công?ự ạ ồ ỏ
- 1 -
H NG D N CH M VÀ ĐÁP ÁNƯỚ Ẫ Ấ
Câu N i dungộĐi mể
Câu 1
(3
đi m)ể
1a.
1cos
tan2
+
=x
x
y
ĐK:
( )
Ζ∈
+≠
+≠
⇔
−≠
+≠
⇔
>+
+≠ k
kx
kx
x
kx
x
kx
ππ
π
π
π
π
π
π
2
2
1cos
2
01cos
2
V y TXĐ: ậ
( )
Ζ∈++= kkkRD
πππ
π
2;
2
\
0.75
0.25
1b.
)3tan( += xy
ĐK:
( ) ( )
Ζ∈+−≠⇔Ζ∈+≠+ kkxkkx
π
π
π
π
3
22
3
V y TXĐ: ậ
( )
Ζ∈+−= kkRD
π
π
3
2
\
0.5
0.5
2a.
4
3
cos
6
3cos
2
2
6
3cos
πππ
=
−⇔
−
=
−xx
( )
Zk
k
x
k
x
kx
kx
∈
+
−
=
+=
⇔
+
−
=
+=
⇔
3
2
36
7
3
2
36
11
2
12
7
3
2
12
11
3
ππ
ππ
π
π
π
π
0.25
0.5
0.25
2b.
22cos2cos122coscos2 2=++⇔=+ xxxx
( )
Zk
kx
kx
kx
kx
xx
∈
+−=
+=
⇔
+−=
+=
⇔
==⇔=⇔
π
π
π
π
π
π
π
π
π
6
6
2
3
2
2
3
2
3
cos
2
1
2cos12cos2
0.25
0.25
0.5
Câu 2
(2
đi m)ể
1.
8
2
1
2
−x
x
S h ng t ng quát: (Đi u ki n ố ạ ổ ề ệ
80
≤≤
k
)
( )
k
k
k
kx
xCT
−
=−
+2
8
81
1
.2
( )
k
k
kk xC 388
8.1.2 −− −=
Ta có:
1538
=⇔=−
kk
V y h s c a s h ng ch a ậ ệ ố ủ ố ạ ứ x5 là:
0.25
0.25
0.25
0.25
- 2 -

( )
10242.1.2. 71
8
1
71
8−=−=− CC
2. Ta có
220
3
12 ==Ω C
a. G i ọA là bi n c : “l y đ c 3 viên bi màu xanh”ế ố ấ ượ
10
3
5==Ω⇒ C
A
Xác su t c n tìm: ấ ầ
( )
22
1
220
10 ==
Ω
Ω
=A
AP
0.25
0.25
b. G i ọB là bi n c “l y đ c ít nh t 2 viên bi màu xanh”ế ố ấ ượ ấ
80. 1
7
2
5
3
5=+=Ω⇒ CCC
B
Xác su t c n tìm:ấ ầ
( )
11
4
220
80 ==
Ω
Ω
=B
BP
0.25
0.25
Câu 3
(1
đi m)ể
G i ọ
( ) ( )
';'' yxATA u==
Ta có:
( )
6;2'
642'
211' A
byy
axx ⇒
=+=+=
=+=+=
G i ọ
( )
dTd u
='
Ta có:
( )
*
4'
1'
4'
1'
−=
−=
⇔
+=
+=
yy
xx
yy
xx
Thay (*) vào d :
032 =+− yx
( ) ( )
010'2'
034'21'
=+−⇔
=+−−−⇔
yx
yx
V y ậd’:
0102 =+− yx
0.5
0.25
0.25
Câu 4
(2
đi m)ể
K
I
N
M
A
B
C
D
G
a. Tìm đ c đi m chung Aượ ể
Tìm đ c đi m chung I là giao đi m c a MN và BDượ ể ể ủ
( ) ( )ABD AMN AI=� �
0.5
0.25
0.25
( ) ( )ABD AMN AI=�
( )AI ABD� �
và
( )AI AMN
AM là đ ng trung tuy n c a ườ ế ủ
∆
ABC nên G
( )AM AMN
Trong (AMN): NG c t AI t i Kắ ạ
Suy ra K là giao đi m c a NG v i (ABD)ể ủ ớ
0.25
0.25
0.25
0.25
Câu 5a
(1
đi m)ể
Ta có:
0.5
- 3 -

( )
=
−
=
⇔
=+++−+
=+++
⇔
=+−
=+
2
2
5
2632
1582
22
15
1
111
11
742
93
d
u
dududu
dudu
uuu
uu
0.5
Câu 6a
(1
đi m)ể
Có 10 cách ch n ng i đàn ông khi đã ch n ng i đàn ôngọ ườ ọ ườ
r i, ch có 1 cách ch n ng i đàn bà là v c a ng i đànồ ỉ ọ ườ ợ ủ ườ
ông đó.
V y ta có 10ậ x 1 = 10 cách ch n.ọ
0.5
0.5
Câu 5b
(1
đi m)ể
( )
14cos44sin3224cos44sin3 xxyxxy −=−⇔+−=
Ph ng trình (1) có nghi m: ươ ệ
222 cba ≥+⇔
( ) ( ) ( )
7352
252243 222
2
≤≤−⇔≤−⇔
≤−⇔−≥−+⇔
yy
yy
V y ậ
7max;3min =−= yy
D
D
0.25
0.25
0.25
0.25
Câu 6b
(1
đi m)ể
1260... 4
7
2
9
2
5
4
9
2
6
3
9=== CCCCCC
(cách ch n).ọ
1
- 4 -




















![Bài tập Toán 9 Cánh diều [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250714/minhtuan02/135x160/49671755585888.jpg)











![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



