1
http://ebook.here.vn - Thư viện sách trực tuyến
Së gi¸o dôc - ®µo t¹o h¶I phßng
®Ò thi thö ®¹i häc
Tr−êng thpt trÇn nguyªn hn M«n to¸n líp 12-lÇn 2 - n¨m häc 2009-2010
Thêi gian lµm bµi : 180’
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
( 07 ñiểm )
Câu I ( 2,0ñiểm) Cho hàm số
(
)
(
)
4 2 2
2 2 5 5
y f x x m x m m
= = + − + − +
1/ Khảo sát sự biến thiên và vẽ ñồ thị (C ) hàm số với m = 1
2/ Tìm các giá trị của m ñể ®å thÞ hµm sè có các ñiểm cực ñại, cực tiểu tạo thành 1 tam giác vuông cân.
Câu II(2.0ñiểm) 1/ Giải hệ phương trình:
2 2
2 2
12
12
x y x y
y x y
− =
2/
Gi¶i bÊt ph−¬ng tr×nh :
)3(log53loglog
2
4
2
2
2
2
−>−− xxx
Câu III
(1.0 ñiểm
) T×m
)
;
0
(
π
∈
x
tho¶ mn ph−¬ng tr×nh: cot x - 1 =
xx
x
x2sin
2
1
sin
tan
1
2cos
2
−+
+
.
Câu IV
(1.0 ñiểm)
Tính tích phân :
22
0
I cos cos 2
x xdx
π
=
∫
Câu V
(1.0 ñiểm)
Cho h×nh chãp S.ABC cã AB = AC = a, BC =
2
a ,
3aSA
=
,
0
SAB SAC 30
= =
.
Gäi M lµ trung ®iÓm SA , chøng minh
( )
SA MBC
⊥
. TÝnh
SMBC
V
PHẦN RIÊNG CHO TỪNG CHƯƠNG TRÌNH ( 03 ñiểm )
(Thí sinh chỉ chọn một trong hai chương trình Chuẩn hoặc Nâng cao ñể làm bài.)
A/ Phần ñề bài theo chương trình chuẩn
Câu VI.a:
(2.0ñiểm)
1,
Trong mÆt ph¼ng to¹ ®é Oxy
c
ho
∆
ABC có ñỉnh A(1;2), ñường trung tuyến BM:
2 1 0
x y
+ + =
và phân
giác trong CD:
1 0
x y
+ − =
. Viết phương trình ñường thẳng BC.
2,
Cho P(x) = (1 + x + x
2
+ x
3
)
5
= a
0
+ a
1
x + a
2
x
2
+ a
3
x
3
+ …+ a
15
x
15
a) Tính S = a
0
+ a
1
+ a
2
+ a
3
+ …+ a
15
b) Tìm hệ số a
10.
Câu VII.a:
(1,0ñiểm) Trong không gian Oxyz cho hai ñiểm A (-1;3;-2), B (-3,7,-18) và mặt phẳng
(P): 2x - y + z + 1 = 0 . Viết phương trình mặt phẳng chứa AB và vuông góc với mp (P).
B/ Phần ñề bài theo chương trình nâng cao
Câu VI.b:
(2 ñiểm)
1, Cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao ñiểm I của hai ñường chéo
nằm trên ñường thẳng y = x. Tìm tọa ñộ ñỉnh C và D..
2,
Cho P(x) = (1 + x + x
2
+ x
3
)
5
= a
0
+ a
1
x + a
2
x
2
+ a
3
x
3
+ …+ a
15
x
15
a) Tính S = a
0
+ a
1
+ a
2
+ a
3
+ …+ a
15
b) Tìm hệ số a
10.
Câu VII.b:
(1.0 ñiểm) Cho hàm số y =
− +
−
2
2 2
1
x x
x
(C)
vµ
d
1
: y =
−
x + m, d
2
: y = x + 3.
Tìm tất cả các giá trị của m ñể (C) cắt d
1
tại 2 ñiểm phân biệt
A,B ñối xứng nhau qua d
2
.
******* HÕt *******
2
http://ebook.here.vn - Thư viện sách trực tuyến
®¸p ¸n vµ biÓu ®iÓm Thi thö ®¹i häc lÇn ii
M«n to¸n líp 12- 2009-2010
Câu ý H−íng dÉn gi¶i chi tiÕt §iÓm
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
7.00
Câu I
2
1
Cho hàm số
(
)
(
)
5522
224
+−+−+=
mmxmxxf (
C
)
Khảo sát sự biến thiên và vẽ ñồ thị hàm số với m = 1
1
1* TXð: D =
R
2*
Sù biÕn thiªn c
ủ
a hàm s
ố
:
* Giíi h¹n t
ạ
i v« c
ự
c
:
(
)
+∞=
−∞→
xf
x
lim :
(
)
+∞=
+∞→
xf
x
lim
0.25
* B¶ng biÕn thiªn:
(
)
(
)
1444''
23
−=−== xxxxyxf
1;1;00'
=
−
=
=
⇔
=
xxxy
x -
∞
-1 0 1 +
∞
y’ - 0 + 0 - 0 +
y +
∞
1 +
∞
0 0
Hµm sè ®ång bi
ế
n trªn m
ỗ
i kho¶ng
(
)
0;1−
vµ
(
)
+∞;1
, ngh
ị
ch bi
ế
n
Trªn m
ỗ
i kho
ả
ng
(
)
1;−∞−
và
(
)
1;0
Hàm s
ố
ñạ
t c
ự
c ti
ể
u t
ạ
i
0;1
=±=
CT
yx
,
ñạ
t c
ự
c
ñạ
i t
ạ
i
1;0
==
CD
yx
0.5
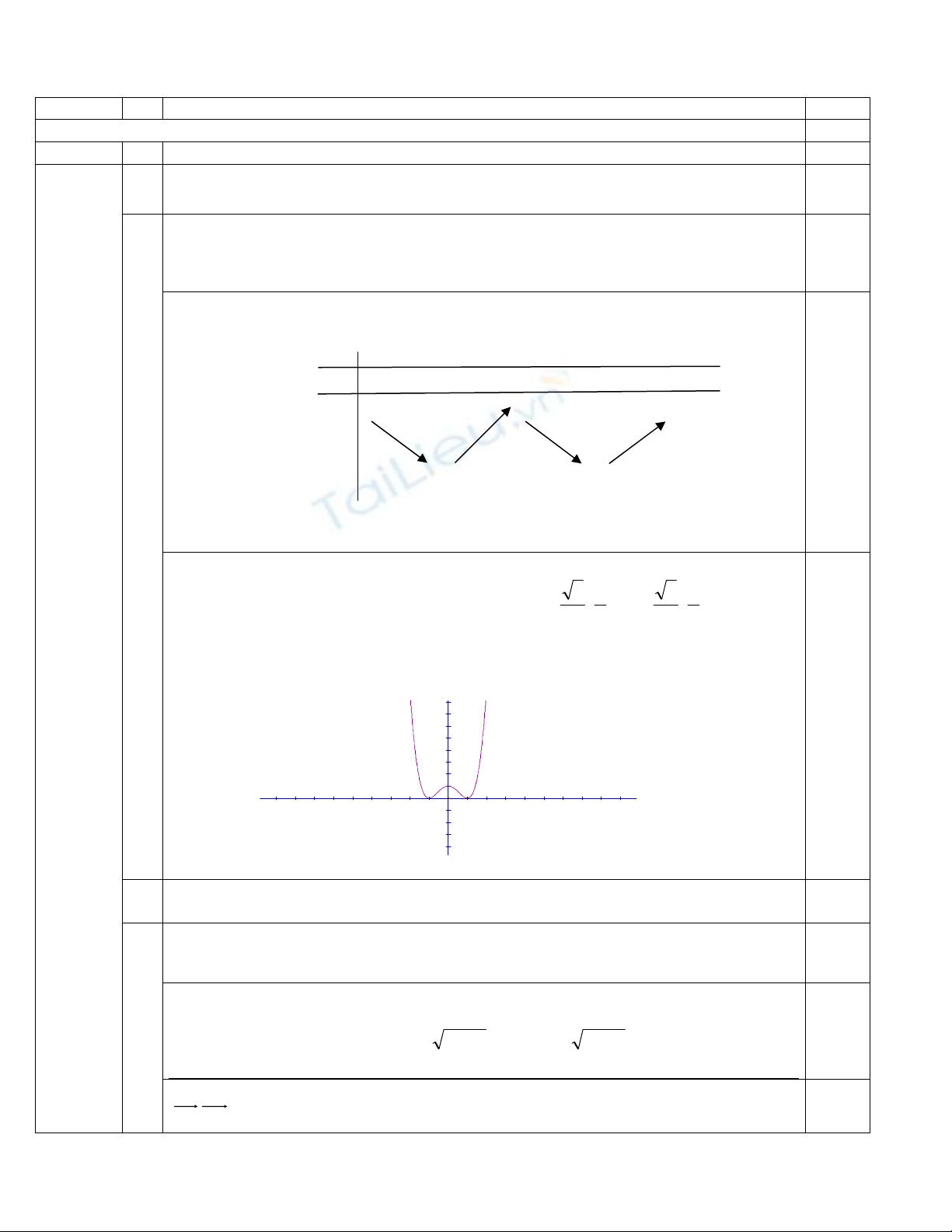
3*
§å thÞ:
* ðiểm uốn: 412''
2
−= xy
, các ñiểm uốn là:
−9
4
;
3
3
,
9
4
;
3
3
21
UU
* Giao ñiểm với các trục toạ ñộ: A(0; 1), B(-1;0) và C(1; 0)
* Hàm số là chẵn trên R nên ñồ thị nhận trục Oy làm trục ñối xứng
*
ðồ thị:
8
6
4
2
-2
-4
-5
5
0.25
2
Tìm các giá trị của m ñể (
C
) có các ñiểm cực ñại, cực tiểu tạo thành 1 tam giác
vuông cân.
1
* Ta có
( ) ( )
3
2
0
' 4 4 2 0 2
x
f x x m x
x m
=
= + − = ⇔
= −
0.25
* Hàm số có Cð, CT khi f’(x)=0 có 3 nghiệm phân biệt và ñổi dấu :
m < 2 (1) . Toạ ñộ các ñiểm cực trị là:
(
)
(
)
(
)
mmCmmBmmA −−−−−+− 1;2,1;2,55;0
2
0.5
* Do tam giác ABC luôn cân tại A, nên bài toán thoả mãn khi vuông tại A:
(
)
1120.
3
=⇔−=−⇔= mmACAB
vì ñk (1)
0.25
3
http://ebook.here.vn - Thư viện sách trực tuyến
Trong ñó
(
)
(
)
44;2,44;2
22
−+−−−=−+−−= mmmACmmmAB
Vậy giá trị cần tìm của m là m = 1.
Câu II
2
1
Giải hệ phương trình:
2 2
2 2
12
12
x y x y
y x y
+ + − =
− =
1
* ðiều kiện:
| | | |
x y
≥
ðặt
2 2
; 0
u x y u
v x y
= − ≥
= +
;
x y
= −
không thỏa hệ nên xét
x y
≠ −
ta có
2
1
2
u
y v
v
= −
. Hệ phương trình ñã cho có dạng:
2
12
12
2
u v
u u
vv
+ =
− =
0.25
4
8
u
v
=
⇔
=
hoặc
3
9
u
v
=
=
+
2 2
4
4
88
ux y
vx y
=
− =
⇔
=+ =
(I) +
2 2
3
3
99
ux y
vx y
=
− =
⇔
=+ =
(II)
0.25
Giải hệ (I), (II).
0.25
Sau ñó hợp các kết quả lại, ta ñược tập nghiệm của hệ phương trình ban ñầu
là
(
)
(
)
{
}
5;3 , 5;4
S=
0.25
2
Gi¶i bÊt ph−¬ng tr×nh :
)3(log53loglog
2
4
2
2
2
2
−>−− xxx 1
§K:
≥−−
>
03loglog
0
2
2
2
2
xx
x
BÊt ph−¬ng tr×nh ® cho t−¬ng ®−¬ng víi
)1()3(log53loglog
2
2
2
2
2
−>−− xxx
®Æt t = log
2
x,
BPT (1)
⇔
)3(5)1)(3()3(532
2
−>+−⇔−>−− tttttt
0.25
<<
−≤
⇔
<<
−≤
⇔
−>−+
>
−≤
⇔4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
0.5
<<
≤<
⇔
168
2
1
0
x
x
VËy BPT ® cho cã tËp nghiÖm lµ: )16;8(]
2
1
;0( ∪
0.25
Câu III
T×m
)
;
0
(
π
∈
x
tho¶ mn ph−¬ng tr×nh:
Cot x - 1 = xx
x
x2sin
2
1
sin
tan
1
2cos
2
−+
+
.
1
§K:
−≠
≠
⇔
≠+
≠
1tan
02sin
0cossin
02sin
x
x
xx
x
0.25
4
http://ebook.here.vn - Thư viện sách trực tuyến
Khi ®ã pt
xxx
x
x
xx
x
xx cossinsin
sin
cos
cos.2cos
sin
sincos
2
−+
+
=
−
⇔
xxxxxx
x
xx cossinsincossincos
sin
sincos
22
−+−=
−
⇔
⇔
)
2
sin
1
(
sin
sin
cos
x
x
x
x
−
=
−
⇔
0)1sincos)(sinsin(cos
2
=−−− xxxxx
0.25
⇔
0
)
3
2
cos
2
)(sin
sin
(cos
=
−
+
−
x
x
x
x
⇔
0
sin
cos
=
−
x
x
⇔
tanx = 1
)(
4
Zkkx ∈+=⇔
π
π
(tm)
( )
4
0;0
π
π
=⇒=⇒∈ xkx
KL:
0. 5
Câu IV
Tính tích phân :
22
0
I cos cos 2
x xdx
π
=
∫
1
2 2 2
2
0 0 0
1 1
I cos cos 2 (1 cos 2 )cos 2 (1 2cos 2 cos 4 )
2 4
x xdx x xdx x x dx
π π π
= = + = + +
∫ ∫ ∫
0.5
/2
0
1 1
( sin 2 sin 4 ) |
4 4 8
x x x
π
π
= + + =
0.5
Câu V Cho h×nh chãp S.ABC cã AB = AC = a, BC = 2
a , 3aSA =,
0
SAB SAC 30
= =
.
Gäi M lµ trung ®iÓm SA , chøng minh
( )
SA MBC
⊥
. TÝnh
SMBC
V
1
Theo ®Þnh lÝ c«sin ta cã:
2 2 2 2 2 0 2
SB SA AB 2SA.AB.cosSAB 3a a 2.a 3.a.cos30 a
= + − = + − =
Suy ra
a
SB
=
. T−¬ng tù ta còng cã SC = a.
0.25
Gäi M lµ trung ®iÓm cña SA , do hai tam gi¸c SAB vµ SAC lµ hai tam gi¸c c©n nªn
MB
⊥
SA, MC
⊥
SA. Suy ra SA
⊥
(MBC).
0.25
Hai tam gi¸c SAB vµ SAC cã ba cÆp c¹nh t−¬ng øng b»ng nhau nªn chóng
b»ng nhau. Do ®ã MB = MC hay tam gi¸c MBC c©n t¹i M. Gäi N lµ trung ®iÓm cña
BC suy ra MN
⊥
BC. T−¬ng tù ta còng cã MN
⊥
SA.
0.25
S
A
B
C
M
N
5
http://ebook.here.vn - Thư viện sách trực tuyến
16
a3
2
3a
4
a
aAMBNABAMANMN
2
2
2
2222222
=
−
−=−−=−=
4
3a
MN =⇒ .
Do ®ã
3
.
1 1 1 3 3
. . . .
3 2 6 2 4 2 32
S MBC
a a a a
V SM MN BC= = = (®vtt)
0.25
PHẦN RIÊNG CHO MỖI CHƯƠNG TRÌNH
3.00
Phần lời giải bài theo chương trình Chuẩn
Câu VIa
2
1 Trong mÆt ph¼ng to¹ ®é Oxy
c
ho
∆
ABC có ñỉnh A(1;2), ñường trung tuyến BM:
2 1 0
x y
+ + =
và phân giác trong CD:
1 0
x y
+ − =
. Viết phương trình ñường
thẳng BC.
1
ðiểm
(
)
: 1 0 ;1
C CD x y C t t
∈ + − = ⇒ −
.
Suy ra trung ñiểm M của AC là 1 3
;
2 2
t t
M
+ −
.
( )
1 3
: 2 1 0 2 1 0 7 7;8
2 2
t t
M BM x y t C
+ −
∈ + + = ⇒ + + = ⇔ = − ⇒ −
0.25
0.25
Từ A(1;2), kẻ
: 1 0
AK CD x y
⊥ + − =
tại I (ñiểm
K BC
∈
).
Suy ra
(
)
(
)
: 1 2 0 1 0
AK x y x y
− − − = ⇔ − + =
.
Tọa ñộ ñiểm I thỏa hệ:
( )
1 0
0;1
1 0
x y I
x y
+ − =
⇒
− + =
.
Tam giác ACK cân tại C nên I là trung ñiểm của AK
⇒
tọa ñộ của
(
)
1;0
K−
.
ðường thẳng BC ñi qua C, K nên có phương trình: 1
4 3 4 0
7 1 8
x y x y
+
= ⇔ + + =
− +
0.25
0.25
2 Cho P(x) = (1 + x + x
2
+ x
3
)
5
= a
0
+ a
1
x + a
2
x
2
+ a
3
x
3
+ …+ a
15
x
15
a) Tính S = a
0
+ a
1
+ a
2
+ a
3
+ …+ a
15
b) Tìm hệ số a
10.
1
Ta có P(1) = a
0
+ a
1
+ a
2
+ a
3
+ …+ a
15
= (1 + 1 + 1 + 1)
5
= 4
5
0.25
Ta có P(x) = [(1 + x)(1 + x
2
)]
5
=
( )
5 5 5 5
2 2
5 5 5 5
0 0 0 0
.
i
k k i k i k i
k i k i
C x C x C C x
+
= = = =
=
∑ ∑ ∑∑
Theo gt ta cã
3
4
2 10
4
0 5,
2
0 5,
5
0
i
k
k i i
k k N k
i i N
i
k
=
=
+ =
=
≤ ≤ ∈ ⇔
=
≤ ≤ ∈
=
=
⇒
a
10
=
0 5 2 4 4 3
5 5 5 5 5 5
. . . 101
C C C C C C+ + =
0.25