SỞ GD VÀ ĐT TPHCM ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2018-2019
ĐỀ MINH HỌA SỐ 9 MÔN: TOÁN
Đề thi gồm 2 trang Thời gian làm bài :120 phút ( không tính thời gian phát đề)
Bài 1: Giải phương trình:
22
3 1 3x x x x
Bài 2: Cho parabol (P):
2
3
4
yx
và đường thẳng (d):
12
2
yx
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Gọi x1, x2 là hoành độ giao điểm của đồ thị (P) và đường thẳng (d) (với x1 > x2).
Tính giá trị biểu thức sau: A = 3x1 + x2
Bài 3: Cho hai đường tròn (O; 5cm) và (O’; 5cm) cắt nhau tại A và B . Tính độ dài dây chung AB biết
OO’ = 8cm
Bài 4: Một vận động viên bơi lội nhảy cầu (xem hình minh họa bên dưới) . Khi nhảy, độ cao h từ
người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu
(tính bằng mét) bởi công thức:
2
14hx
. Hỏi khoảng cách x bằng bao nhiêu:
a) Khi vận động viên ở độ cao 3m?
b) Khi vận động viên chạm mặt nước?
Bài 5: Vào khoảng năm 200 trước Công nguyên, Ơ-ra-tô-xten, một nhà toán học và thiên văn học
Hi lạp đã ước lượng được "chu vi" của Trái Đất (chu vi đường xích đạo) nhờ hai quan sát sau:
a) Một ngày trong năm, ông để ý thấy Mặt Trời chiếu
thẳng các đáy giếng ở thành phố Xy-en (nay gọi là
Át-xu-an), tức là tia sáng chiếu thẳng đứng
b) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en
800km, một tháp cao 25m có bóng trên mặt đất dài
3,1m
Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của
Trái Đất (Trên hình), điểm S tượng trưng cho thành phố
Xy-en, điểm A tượng trưng cho thành phố A-lếch-
xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn
x
h
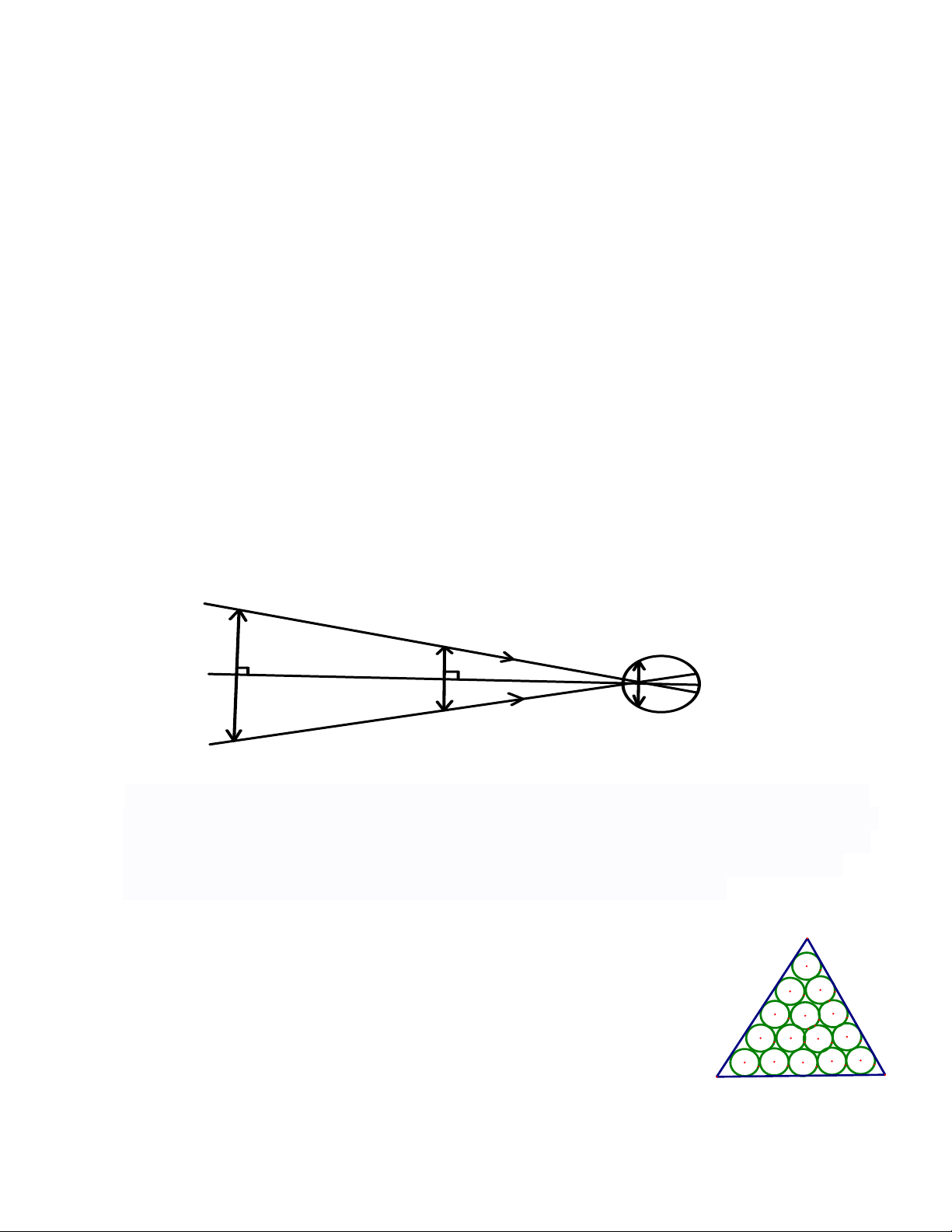
thẳng AB
Bài 6:
a) Để giúp gia đình trang trải chi phí học tập , bạn An xin làm thêm tại một quán nọ và bạn ấy
được trả 40 000 đồng cho mỗi giờ làm việc tại quán. Hỏi sau 1 tuần làm việc bạn An nhận
được bao nhiêu tiền? Biết rằng bạn làm hết tuần không nghỉ ngày nào và do phải đi học nên
mỗi ngày bạn chỉ làm 4 tiếng.
b) Nếu mỗi giờ làm thêm tăng ca bạn An được trả thêm 50% số tiền mà mỗi giờ bạn ấy kiếm
được trong giờ làm việc bình thường thì trong tuần đó mỗi ngày bạn phải làm thêm bao nhiêu
giờ để sau một tuần bạn được trả 1 960 000 đồng? (An làm tăng ca tất cả các ngày trong tuần,
số giờ tăng ca mỗi ngày là như nhau)
Bài 7: Có hai quặng sắt: quặng I chứa 70% sắt, quặng II chứa 40% sắt. Người ta trộn một lượng
quặng loại I với một lượng quặng loại II thì được hỗn hợp quặng chứa 60% sắt. Nếu lấy tăng
hơn lúc đầu 5 tấn quặng loại I và lấy giảm hơn lúc đầu 5 tấn quặng loại II thì được hỗn hợp
quặng chứa 65% sắt. Tính khối lượng mỗi loại quặng đem trộn lúc đầu?
Bài 8: Mắt nhìn hai vật A1B1 và A2B2 ở xa, gần khác nhau nhưng do chiều cao ảnh của chúng trên
màng lưới bằng nhau (hình minh họa bên dưới) nên mắt nhìn thấy hai vật đó có chiều cao như
nhau. Cho biết vật A2B2 có chiều cao A2B2 = 1,2m và ở cách mắt đoạn OH2 = 2m, vật A1B1 ở
cách mắt đoạn OH1 = 500m. Hỏi vật A1B1 có chiều cao bao nhiêu?
Bài 9: Có 480 học sinh dự trại hè tại 3 địa điểm. 10% số học sinh ở địa điểm 1; 8,5% số học sinh ở
địạ điểm 2; 15% số học sinh ở địa điểm 3 đi thăm viện bảo tàng. Viện bảo tàng cách địa điểm
một 60 km, cách địa điểm hai 40 km, cách địa điểm ba 30 km. Để trả vừa đủ tiền xe, giá 100
đồng cho mỗi người đi 1 km, số người đi thăm viện bảo tàng đã góp đồng đều mỗi người
4000 đồng. Hỏi có bao nhiêu người ở mỗi địa điểm đi thăm viện bảo tàng?
Bài 10:
Có 15 quả bi-a hình cầu đặt nằm trên mặt bàn, sao cho
chúng được dồn khít trong một khung hình tam giác
đều có chu vi bằng 858mm (hình vẽ bên dưới).
Tính bán kính của mỗi quả bi-a?
-HẾT-
H2
H1
B'
A'
O
B2
A2
B1
A1
BÀI GIẢI CHI TIẾT
Bài 1: Giải phương trình:
22
3 1 3x x x x
Bài giải chi tiết:
Ta có: Phương trình:
2 2 2 2
3 1 3 3 1 3x x x x x x x x
Đặt:
2
t x x
, ta được phương trình:
2222
2
30 33
3 1 3 9 1 6 9 9 9 6 9
3 1 3
3
3
3
30
0
30
30 30 3
ttt
tt t t t t t t
tt
t
t
t
ttn
t
tt
tt ttn

 











Với t = 0, ta có:
200
0 1 0 1 0 1
xx
x x x x xx




Với t = 3, ta có:
22
21
1
1
3 3 0 1; 1; 3
4 1 4.1.( 3) 13 0
1 13
2. 2
1 13
2. 2
x x x x a b c
b ac
b
xa
b
xa


Thử lại các kết quả vừa tìm được, ta thấy đều thỏa mãn phương trình.
(Ví dụ các em thử x = 0 vào phương trình:
22
3 0 0 1 0 0 3 3 3
(luôn đúng))
Vậy nghiệm của phương trình là:
1 13 1 13
1; 0; ,
22
S





Bình luận bài toán:
Đây là dạng bài tập tương đối mới với nhiều em. Tỉ lệ ra trong đề là rất thấp. Tuy nhiên, tôi mạo
hiểm đưa vào cho các em ôn tập làm “vũ khí phòng thủ”, một phần giúp các em không bỡ ngỡ
khi gặp trong quá trình học tập trên lớp cũng như trong đề thi (nếu có).
Các em lưu ý, vì ban đầu chúng ta chưa có điều kiện cho bài toán, nên khi tìm ra giá trị của x các
em phải thế vào phương trình xem có thỏa mãn phương trình không rồi mới kết luận nghiệm.
Bài 2: Cho parabol (P):
2
3
4
yx
và đường thẳng (d):
12
2
yx
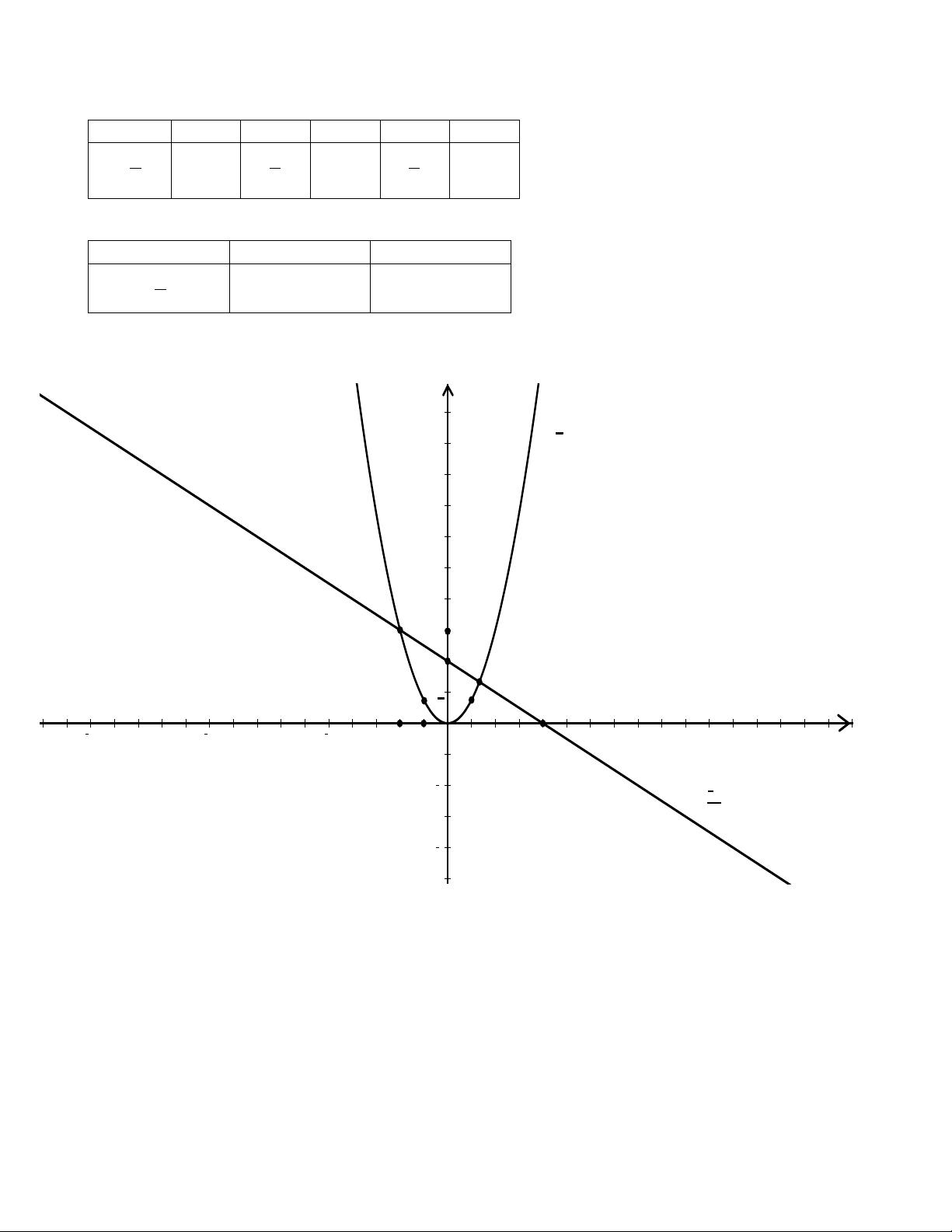
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Gọi x1, x2 là hoành độ giao điểm của đồ thị (P) và đường thẳng (d) (với x1 > x2).
Tính giá trị biểu thức sau: A = 3x1 + x2
Bài giải chi tiết:
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
Bảng giá trị
x
- 2
- 1
0
1
2
2
3
4
yx
3
4
3
4
3
x
-2
4
12
2
yx
3
0
Đồ thị
b) Gọi x1, x2 là hoành độ giao điểm của đồ thị (P) và đường thẳng (d) (với x1 > x2).
Tính giá trị biểu thức sau: A = 3x1 + x2
Phương trình hoành độ giao điểm của (P) và (d):
10
8
6
4
2
2
4
15 10 5 5 10 15
O
x
y
3
1
-1
3
4
4-2
y =
1
2∙x + 2
y =
3
4∙x2
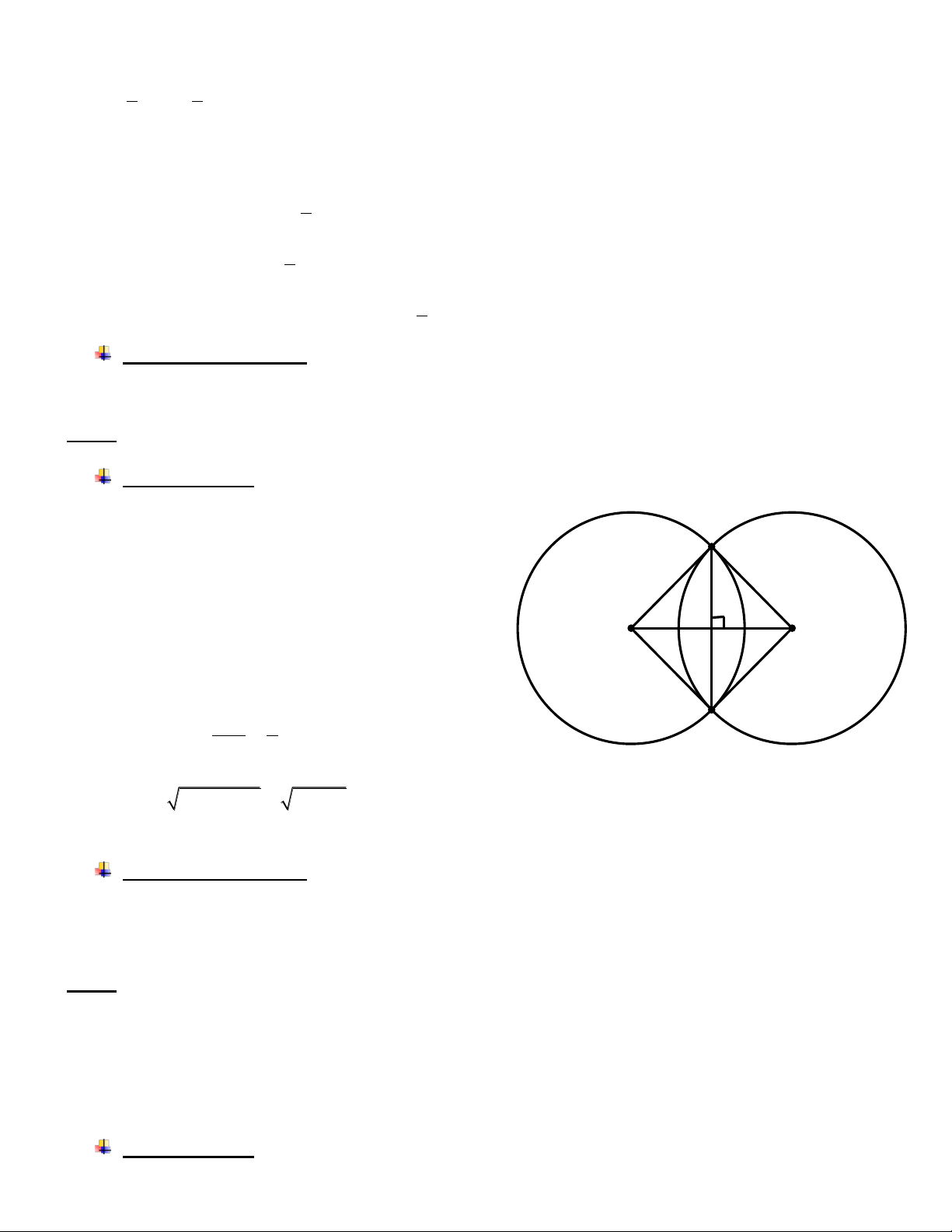
2 2 2 2
2
1 2 1 2
31
2 3 2 8 3 2 8 0
42
3 6 4 8 0 3 2 4 2 0 2 3 4 0
2
20 4
3 4 0 3
4
: ; 2
3
x x x x x x
x x x x x x x x
x
x
xx
Do x x x x




Thế vào A = 3x1 + x2, ta được:
4
3. 2 2
3
A
Bình luận về bài toán:
Đây là một bài tập quen thuộc với các em. Các em chỉ lưu ý câu b, phải xem yêu cầu của đề để
chọn ra x1 và x2 tương ứng.
Bài 3: Cho hai đường tròn (O; 5cm) và (O’; 5cm) cắt nhau tại A và B . Tính độ dài dây chung AB biết
OO’ = 8cm
Bài giải chi tiết:
Gọi I là giao điểm của OO’ và AB.
Ta có:
5OA OB cm R
' ' 5 'O A O B cm R
' ' 5OA OB O A O B cm
Tứ giác OAO’B là hình thoi (tứ giác có 4
cạnh bằng nhau)
'AB OO
tại I
I là trung điểm của OO’ và AB
'8
'4
22
OO
IO IO cm
Xét tam giác vuông OAI, áp dụng định lý Pitago ta có:
2 2 2 2
5 4 1AI OA OI cm
2 2.1 2AB AI cm
Vậy: Độ dài dây chung AB là 2cm.
Bình luận về bài toán:
Đây là một bài tập cơ bản, chủ yếu xoay quanh các tính chất của hình thoi. Nếu từ đầu các em
không nhận ra và chứng minh ra được hình thoi OAO’B thì bài toán sẽ dài hơn.
Các em cũng có thể dùng tính chất đường trung trực để giải bài này.
Bài 4: Một vận động viên bơi lội nhảy cầu (xem hình minh họa bên dưới) . Khi nhảy, độ cao h từ
người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu
(tính bằng mét) bởi công thức:
2
14hx
. Hỏi khoảng cách x bằng bao nhiêu:
a) Khi vận động viên ở độ cao 3m?
b) Khi vận động viên chạm mặt nước?
Bài giải chi tiết:
I
B
A
O'
O