SỞ GD VÀ ĐT TPHCM ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2018-2019
ĐỀ MINH HỌA SỐ 11 MÔN: TOÁN
Đề thi gồm 2 trang Thời gian làm bài :120 phút ( không tính thời gian phát đề)
Bài 1: Bạn Tý và Quân cùng tham gia giải Lê Quý Đôn trên báo Khăn Quàng Đỏ đang tranh luận về một bài toán.
Bạn Tý nói: “Để biểu thức A có giá trị nguyên thì
16;49;36x
”. Bạn Quân cho rằng:
16;49;25;1x
. Hãy trình
bày ý kiến của em, biết rằng:
2 9 3 2 1 0; 4; 9
5 6 2 3
x x x
A x x x
x x x x
Bài 2:
Dựng một cái thang lên tường với độ cao là 3m, thì khoảng cách từ
chân thang tới chân tường tối thiểu là bao nhiêu để đảm bảo an toàn?
Khi đó, em hãy tính chiều dài của cái thang? Biết rằng để có sự an
toàn thì hệ số góc của cầu thang tối đa là 4.
Bài 3: Cho đường tròn (O, 3cm) và đường tròn (O’, 1cm) tiếp xúc ngoài tại
A. Vẽ hai bán kính OB, O’C song song với nhau thuộc cùng một nửa mặt phẳng có bờ OO’.
a) Tính số đo góc BAC.
b) Gọi I là giao điểm của BC và OO’. Tính độ dài OI.
Bài 4: Một xe ôtô chuyển động theo phương trình
2
60 4S t t
, trong đó S( km) là quãng đường xe đi được trong
thời gian t (giờ), t là thời gian chuyển động của xe tính từ lúc 11h sáng. Xem như xe chuyển động trên một
đoạn đường thẳng và không nghỉ.
a) Hỏi từ lúc 11h30phút đến lúc13h15phút xe đã đi được quãng đường dài bao nhiêu km?
b) Đến lúc mấy giờ thì xe đi được quãng đường dài 64km (tính từ lúc 11h)?
Bài 5: Hai cây cọ mọc đối diện nhau ở hai bờ sông, một cây cao 30m, một cây cao 20m. Trên đỉnh mỗi cây có 1 con
chim đang đậu. Chợt có 1 con cá xuất hiện trên sông giữa hai cây cọ. Cả hai con chim lập tức bay xuống và
vồ mồi cùng một lúc. Hỏi con cá cách gốc mỗi cây cọ bao nhiêu mét biết rằng hai gốc cây cách nhau 50m?
Xem vận tốc bay của hai con chim là nhau.
50m
20m
30m
EC
D
B
A
x=?
3m
Bài 6:
a) Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 5 quyển tập và 2 cây bút. Nhưng khi ra đến nơi,
giá quyển tập mà bạn An dự định mua đã tăng lên 1000 đồng một quyển còn giá một cây bút thì giảm 500
đồng một cây so với dự định. Vậy để mua 5 quyển tập và 2 cây bút như dự định ban đầu thì bạn An còn thừa
hay thiếu số tiền là bao nhiêu?
b) Một tổ mua nguyên vật liệu để tổ chức thuyết trình tại lớp hết 72.000 đồng, chi phí được chia đều cho mỗi
thành viên của tổ. Nếu tổ giảm bớt 2 người thì mỗi người phải đóng thêm 3.000 đồng. Hỏi số người của tổ?
Bài 7: Một bóng đèn sợi đốt giá 5000 đồng có công suất 60W và thời gian thắp
sáng tối đa là 1000h. Một bóng đèn compact giá 50.000 đồng có công suất
15W và thời gian thắp sáng tối đa là 8000h. Hai đèn có độ sáng tương
đương nhau. Giá tiền 1KW.h điện là 1800 đồng. Tính chi phí cho việc sử
dụng mỗi loại đèn trên trong 8000h.
Bài 8: Người ta cho thêm 1kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là
20%
(nồng độ axit là tỉ
số khối lượng axit so với khối lượng dung dịch). Sau đó lại cho thêm 1kg axit vào dung dịch B thì được dung
dịch C nồng độ axit là
1
33 %
3
. Tính nồng độ axit trong dung dịch A?
Bài 9: Tổng kết học kỳ 2, trường trung học cơ sở N có 60 học sinh không đạt học sinh giỏi trong đó có 6 em từng đạt
học sinh giỏi học kỳ 1; số học sinh giỏi của học kỳ 2 bằng
40
37
số học sinh giỏi học kỳ 1 và 8% số học sinh của
trường không đạt học sinh giỏi của học kỳ 1 nhưng đạt học sinh giỏi của học kỳ 2. Tìm số học sinh giỏi của
học kỳ 2 của trường, biết số học sinh của trường không thay đổi trong suốt năm học.
(Trích đề thi vào PTNK TPHCM )
Bài 10:
a) Lớp 9A có 27 học sinh nam và 18 học sinh nữ. Nhân dịp sinh nhật của bạn X ( là một thành viên của lớp), các
bạn trong lớp có rất nhiều món quà tặng X. Ngoài ra mỗi bạn nam của lớp làm 3 tấm thiệp và mỗi bạn nữ xếp
2 hoặc 5 con hạc để tặng bạn X. Biết số tấm thiệp và số con hạc bằng nhau, hỏi bạn X là nam hay nữ?
b) Sóng cực ngắn có tần số 30 -30000MHz. Năng lượng rất lớn, không bị tầng điện ly hấp thụ, truyền đi rất xa (>
2200km) theo đường thẳng . Dùng trong thông tin liên lạc vũ trụ, ra đa và truyền hình. Tại một thời điểm có
hai vệ tinh đang ở hai vị trí A và B cùng cách mặt đất 230km, một tín hiệu (truyền bằng sóng cực ngắn) được
truyền đi từ vệ tinh A truyền đến vệ tinh B theo phương AB. Hỏi vệ tinh B có nhận được tín hiệu đó không?
Biết khoảng cách giữa A và B theo đường thẳng là 2200km và bán kính Trái Đất là 6400km.
O
B
A
2200km
BÀI GIẢI CHI TIẾT
Bài 1: Bạn Tý và Quân cùng tham gia giải Lê Quý Đôn trên báo Khăn Quàng Đỏ đang tranh luận về một bài toán.
Bạn Tý nói: “Để biểu thức A có giá trị nguyên thì
16;49;36x
”. Bạn Quân cho rằng:
16;49;25;1x
.
Hãy trình bày ý kiến của em, biết rằng:
2 9 3 2 1 0; 4; 9
5 6 2 3
x x x
A x x x
x x x x
Bài giải chi tiết:
Rút gọn biểu thức A
2 9 3 2 1
5 6 2 3
2 9 3 2 1
2 3 6 2 3
2 9 3 2 1
23
2 3 2
3 3 2 1 2
29
2 3 2 3 3 2
2 9 9 2 4 2
2 3 2 3 2 3
2 9 9 2 4 2
23
2
23
x x x
A
x x x x
x x x
x x x x x
x x x
xx
x x x
x x x x
x
x x x x x x
x x x x x
x x x x x x
x x x x x
xx
xx
xx
x




22
23
22
23
21
23
1
3
xx
xx
x x x
xx
xx
xx
x
x





Ta có:
1 3 3 1 3 4 4
1
3 3 3 3 3
x x x
Ax x x x x
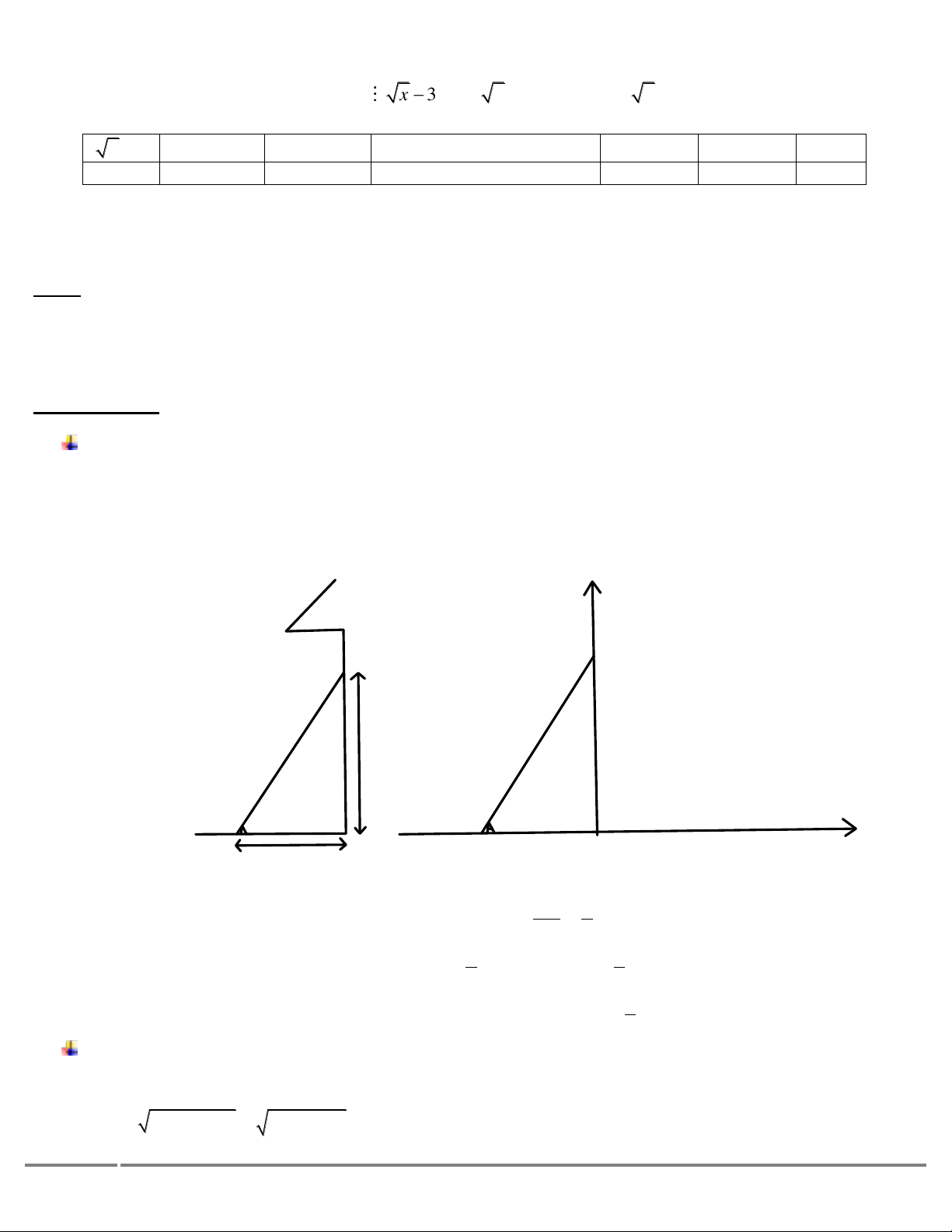
Để biểu thức A có giá trị nguyên
43x
3x
Ư(4)
3 4; 2; 1x
3x
-4
-2
-1
2
4
x
1
4 (loại do điều kiện)
25
49
Vậy: Để biểu thức A có giá trị nguyên thì:
1; 16; 25; 49x
, nên ý kiến của bạn Quân đúng.
Bài 2:
Dựng một cái thang lên tường với độ cao là 3m, thì khoảng cách từ chân thang tới chân tường tối thiểu là bao
nhiêu để đảm bảo an toàn? Khi đó, em hãy tính chiều dài của cái thang? Biết rằng để có sự an toàn thì hệ số
góc của cầu thang tối đa là 4.
Bài giải chi tiết:
Tìm khoảng cách từ chân thang tới chân tường tối thiểu để đảm bảo an toàn.
Gọi x là khoảng cách từ chân thang chân tường
Xét hệ tọa độ Oxy như trong hình vẽ.
Ta có: A(-x ; 0) là giao điểm của đường thẳng (diễn tả cái thang) với trục Ox và T(0; 3) là điểm thuộc
đường thẳng có tung độ dương (giao điểm của cái thang với trục Oy).
Ta có: Đường thẳng nêu trên có hệ số góc
3
tan OAT OT
aOA x
Theo giả thiết , để đảm bảo an toàn thì
4a
nên
33
4 3 4 4
xx
x
Vậy: Khoảng cách x tối thiểu từ chân thang tới chân tường phải là
30,75
4
xm
Tính chiều dài của cái thang
Ta có: OA = 0,75m, OT = 3m
Áp dụng dịnh lý Pitago cho tam giác vuông AOT, vuông tại O, ta có:
2 2 2 2
0,75 3 3,1AT OA OT m
y
x
O
T(0; 3)
A(-x; 0)
3m
x
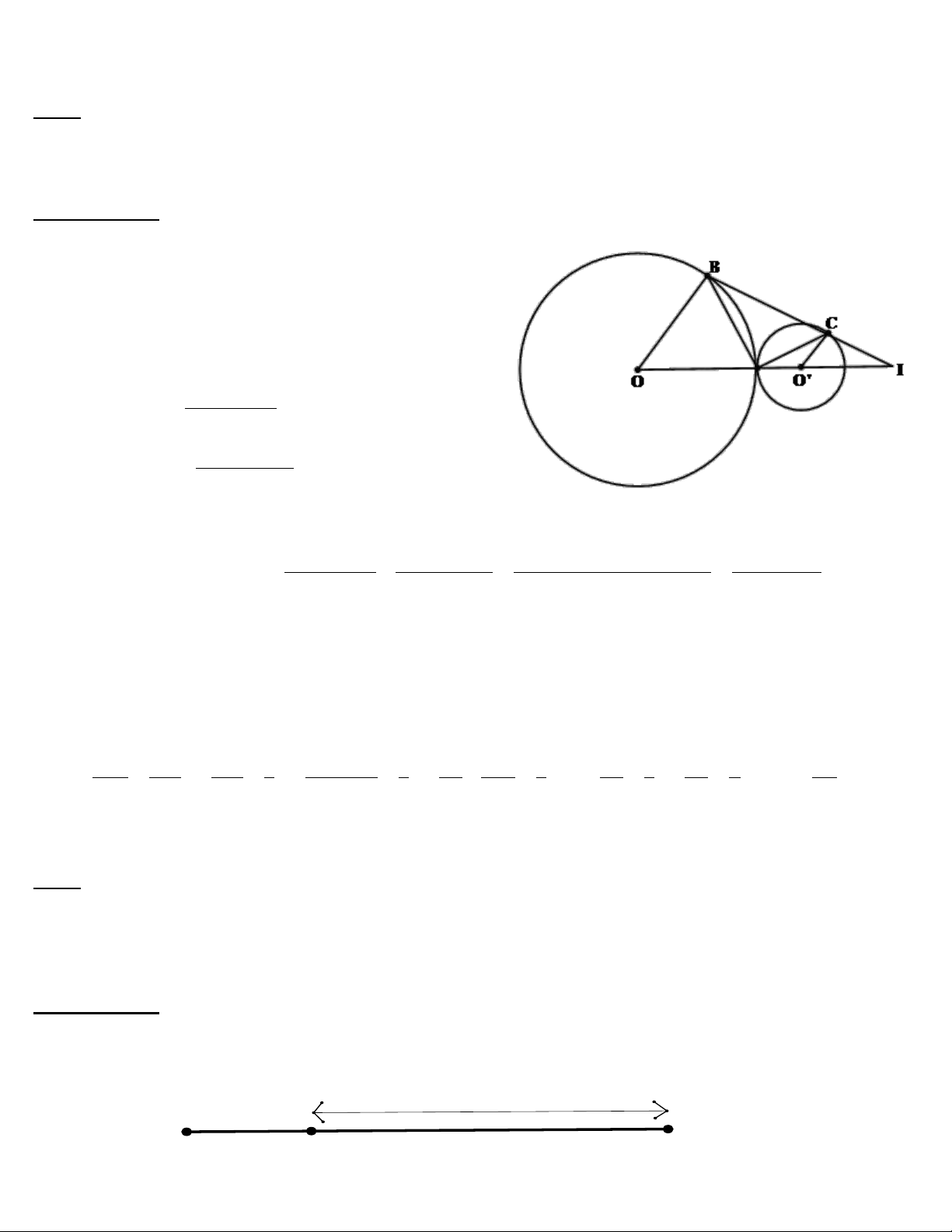
Vậy: Ứng với x = 0,75m thì chiều dài của cái thang khi đó là 3,1 m
Bài 3: Cho đường tròn (O, 3cm) và đường tròn (O’, 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB, O’C song song
với nhau thuộc cùng một nửa mặt phẳng có bờ OO’.
a) Tính số đo góc BAC.
b) Gọi I là giao điểm của BC và OO’. Tính độ dài OI.
Bài giải chi tiết:
a) Tính số đo góc BAC.
Tam giác OAB có OA = OB ( =R ) nên là tam giác
cân tại O.
Tam giác O’AC có O’A = O’C ( =R’ ) nên là tam
giác cân tại O’.
Do đó, ta có:
Góc
^
0
180
2
AOB
OAB
Góc
^
0
180 'C
'2
AO
O AC
Mặt khác, theo giả thiết OB// O’C
góc AOB + góc AO’C = 1800 ( tổng hai góc trong cùng phía)
Góc OAB + góc O’AC =
^^
0
0 0 0 0 0
360 '
180 180 'C 360 180 90
2 2 2 2
AOB AO C
AOB AO
0
90BAC
Lưu ý: ký hiệu
""
là ký hiệu của góc
b) Gọi I là giao điểm của BC và OO’. Tính độ dài OI.
Do đường tròn (O, 3cm) và đường tròn (O’, 1cm) tiếp xúc ngoài tại A
' ' 3 1 4OO R R cm
Trong tam giác OIB, ta có: O’C // OB.
Theo định lý Ta-let, ta có:
' ' ' 1 ' 1 ' 1 4 1 4 2 4.3
16
3 3 3 3 3 2
O C O I O I OI OO OI OO OI cm
OB OI OI OI OI OI OI OI
Vậy : Độ dài đoạn O I = 6cm
Bài 4: Một xe ôtô chuyển động theo phương trình
2
60 4S t t
, trong đó S( km) là quãng đường xe đi được trong
thời gian t (giờ), t là thời gian chuyển động của xe tính từ lúc 11h sáng. Xem như xe chuyển động trên một
đoạn đường thẳng và không nghỉ.
a) Hỏi từ lúc 11h30phút đến lúc13h15phút xe đã đi được quãng đường dài bao nhiêu km?
b) Đến lúc mấy giờ thì xe đi được quãng đường dài 64km (tính từ lúc 11h)?
Bài giải chi tiết:
a) Hỏi từ lúc 11h30phút đến lúc13h15phút xe đã đi được quãng đường dài bao nhiêu km?
A
?km
13h15phút
11h30phút
11h