S GIÁO DC VÀ ðÀO TO ð THI TUYN SINH VÀO LP 10
BN TRE TRUNG HC PH THÔNG CÔNG LP
NĂM HC 2017– 2018
ð Môn : TOÁN (chung)
Thi gian: 120 phút (không k phát ñ)
Câu 1. (2 ñim)
Không s dng máy tính cm tay:
a) Tính
5
18 2 2
2
− + ;
b) Gii h phương trình:
3 1
2 5
x y
x y
− =
+ =
Câu 2. ( 2 ñim)
Trong mt phng ta ñ Oxy cho parabol (P): y = – 2x2 và ñưng thng (d) : y = 2x – 4.
a) V ñ th ca (P) và (d) trên cùng mt phng ta ñ;
b) Bng phương pháp ñi s, hãy tìm ta ñ giao ñim ca (P) và (d) .
Câu 3. ( 2.5 ñim)
Cho phương trình x2 – 2(m – 1)x – (2m + 1) = 0 (1) (m là tham s)
a) Gii phương trình (1) vi m = 2;
b) Chng minh rng phương trình (1) luôn có hai nghim phân bit vi mi m;
c) Tìm m ñ phương trình (1) luôn có hai nghim bng nhau v giá tr tuyt ñi và trái
du nhau.
Câu 4. ( 3.5 ñim)
Cho ñưng tròn O, ñưng kinh AB. Tren tip tuyn ca ñưng tròn (O) ti A ly
ñim M (M khác A). T M v tip tuyn th hai MC vi ñưng tròn (O) (C là tip ñim). K
CH
⊥
AB (H
∈
AB), MB ct ñưng tròn (O) ti ñim th hai là K và ct CH ti N. Chng
minh rng:
a) T giác AKNH ni tip trong mt ñưng tròn;
b) AM2 = MK. MB ;
c)
KAC OMB
=;
d) N là trung ñim ca CH.
HT
GI Ý GII VÀ D KIN THANG ðIM
Câu
Ý Ni dung ðim
5
18 2 2
2
− + =
5 2
3 2 2 2
2
− + 0,50
a)
(1,00)
= (3 – 2 +
5
2
)
2
=
7 2
2
0,50
3 1
2 5
x y
x y
− =
+ =
⇔
6 2 2
2 5
x y
x y
− =
+ =
0,25
⇔
7 7
2 5
x
x y
=
+ =
⇔
1
2
x
y
=
=
0,50
1
b)
(1,00)
Vy h phương trình có nghim:
1
2
x
y
=
=
0,25
V (P): y = – 2x2:
Bng giá tr ca (P):
x -2 -1 0 1 2
y = – 2x2-8 -2 0 -2 -8
0,25
V (d): y = 2x – 4:
Cho x = 0
⇒
y = – 4
⇒
(0; – 4)
Cho y = 0
⇒
x = 2
⇒
(2; 0)
V (d) ñi qua (0; – 4) và (2; 0).
0,25
a)
(1,00)
-4
-8
-2
02
1-1-2
y
x
(d)
(P)
0,50
Phương trình hoành ñ giao ñim ca (P) và (d): – 2x2 = 2x – 4 0,25
⇔
2x2 + 2x – 4 = 0 0,25
⇔
1
2
x 1
x 2
=
=−
⇒
1
2
y 2
y 8
= −
=−
0,25
2
b)
(1,00)
Vy ta ñ giao ñim ca (P) và (d) là: (1; –2) và (– 2; –8). 0,25
Vi m = 2, phương trình tr thành: x2 – 2x – 3 = 0 0,25
Phương trình có: a – b + c = 1 – (– 2) + (– 3) 0,25
⇒
pt có 2 nghim: 1
2
x 1
x 3
= −
=
0,25
a)
(1,00)
Vy khi m = 2, pt (1) có hai nghim phân bit: x1 = – 1; x2 = 3. 0,25
Pt (1) có:
'
∆
= [– (m – 1)]2 – 1. [– (2m + 1)] = m2 + 2 > 0,
∀
m. 0,50
b)
(0,75)
Vy phương trình (1) luôn có hai nghim phân bit vi mi m. 0,25
Theo h thc Vi-ét:
( )
1 2
1 2
S x x 2m 2
P x x 2m 1
= + = −
= = − +
0,25
Theo ñ bài ta có x1, x2 là hai nghim ñi nhau
⇔
S 0
P 0
=
<
⇔
( )
2m 2 0
2m 1 0
− =
− + <
⇔
m 1
1
m
2
=
> −
⇔
m = 1 (*) 0,25
3
c)
(0,75)
Vy khi m = 1, pt (1) có 2 nghim bng nhau v giá tr tuyt ñi và trái du
nhau. 0,25
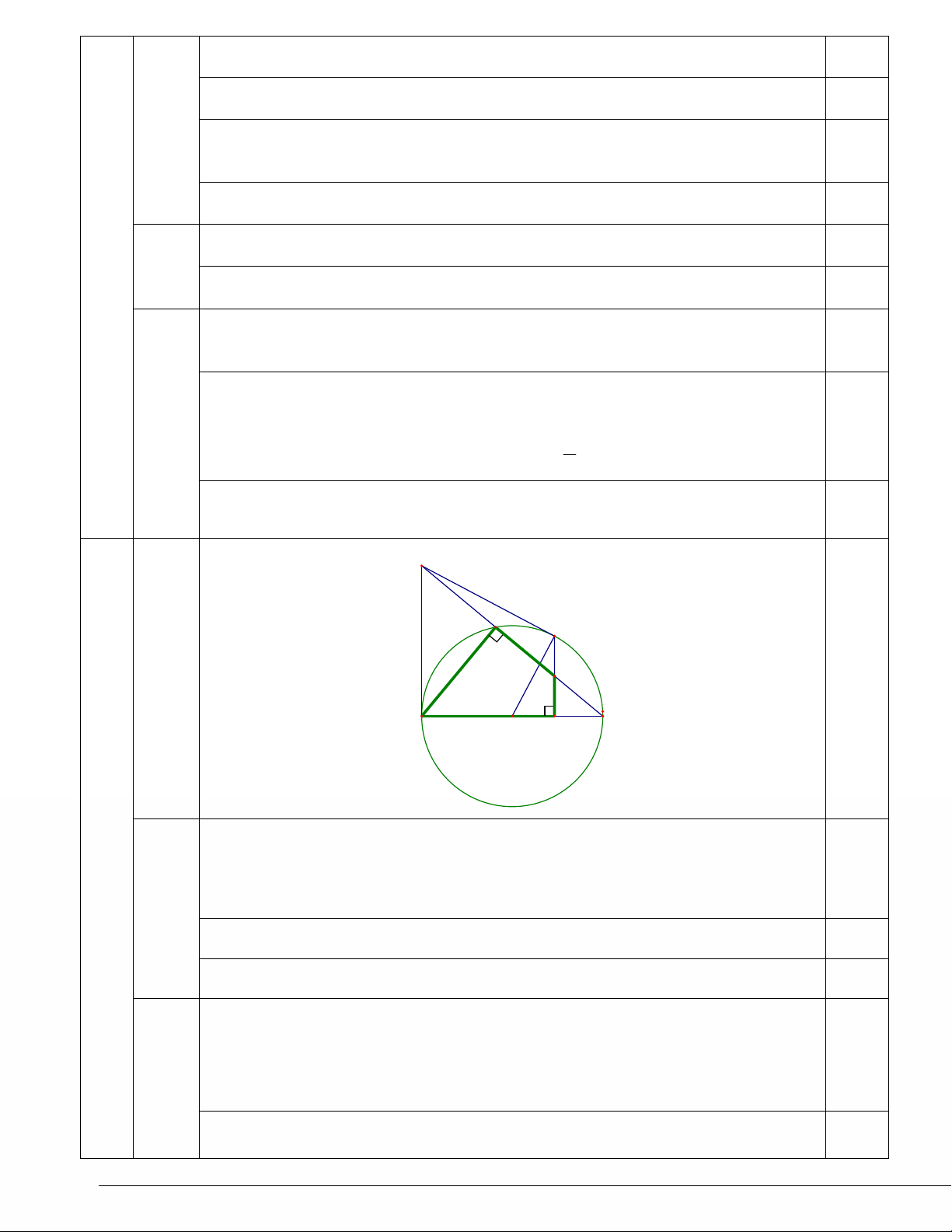
Hình
(0,50)
N
K
H
M
B
O
A
C
Hình
v
ñn
câu b
0,25
Chng minh rng t giác AKNH ni tip:
AKB
= 900 (góc ni tip chn na ñưng tròn),
AHN
= 900 (CH
⊥
AB) 0,50
⇒
AKB
+
AHN
= 18000,25
a)
(1,00)
Vy t giác AKNH ni tip ñư!c ñưng tròn. 0,25
Chng minh rng AM2 = MK. MB:
ABM
∆
vuông ti A có AK
⊥
MB
0,25
4
b)
(0,50)
⇒
AM2 = MK. MB (H thc lư!ng trong tam giác vuông) 0,25
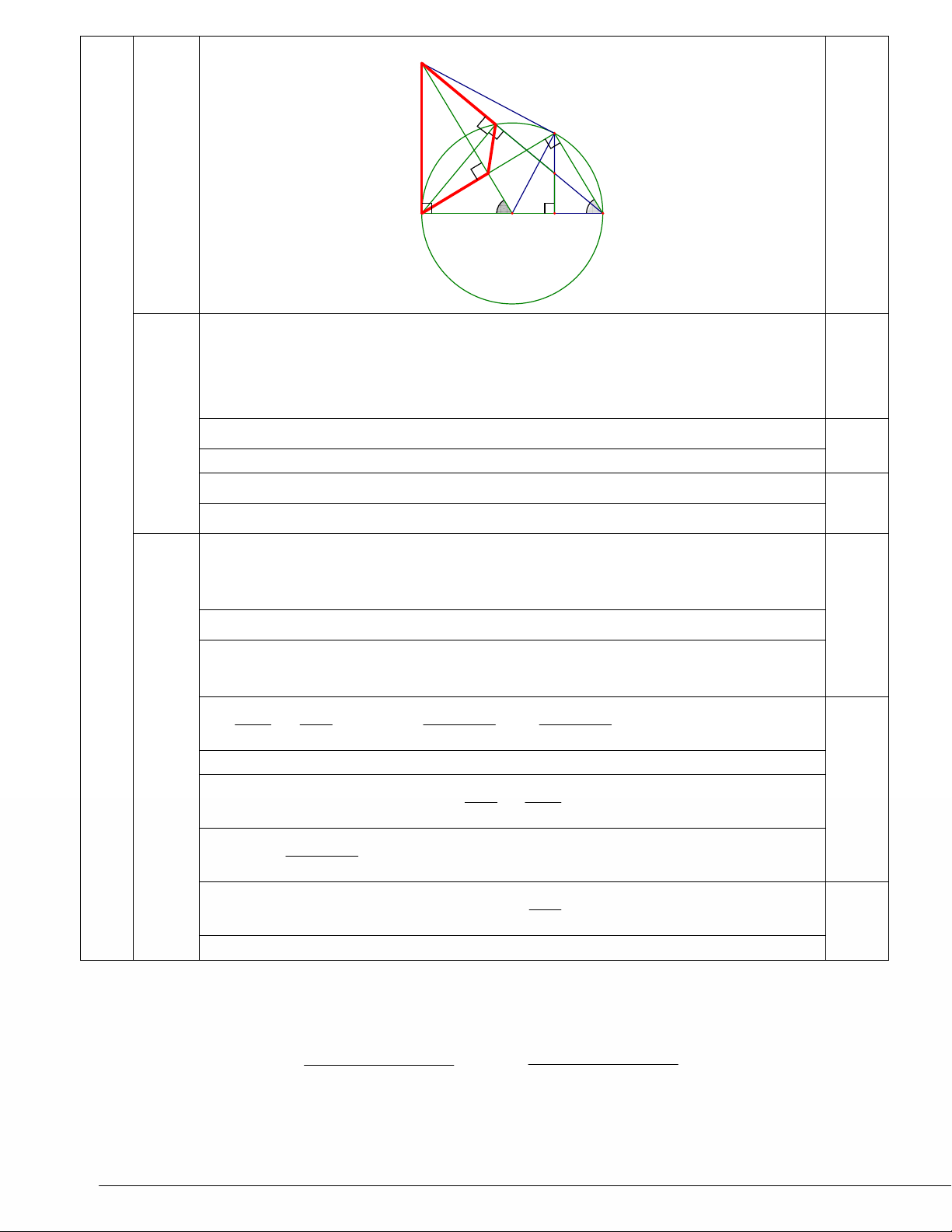
I
N
K
H
M
B
O
A
C
0,25
Chng minh rng
KAC OMB
=:
Gi I là giao ñim ca AC và OM.
MA = MC (tính cht ca 2 tip tuyn ct nhau) và OA = OC = R
⇒
OM là ñưng trung tr"c ca AC
⇒
OM
⊥
AC 0,25
Ta có:
=
MKA
= 900 nhìn ñon MA
⇒
T giác AMKI ni tip ñưng tròn ñưng kính MA 0,25
Trong ñưng tròn ñưng kính MA:
KAI
=
KMI
(ni tip cùng chn
IK
)
c)
(0,75)
⇒
KAC
=
OMB
0,25
Chng minh rng N là trung ñim ca CH:
ACB
= 900 (góc ni tip chn na ñưng tròn)
⇒
BC
⊥
AC
OM
⊥
AC (cmt)
⇒
OM // BC
⇒
AOM
=
HBC
(so le trong)
∆
AOM và
∆
HBC có:
AOM
=
HBC
và
OAM
=
BHC
= 900
⇒
∆
AOM ∽
∆
HBC (g.g) 0,25
⇒
AM
HC
=
OA
BH
⇒
HC =
AM .BH
OA
= 2.
AM .BH
AB
(1)
MA
⊥
AB và CH
⊥
AB
⇒
CH // MA
∆
ABM có CH // MA (cmt)
⇒
BH
BA
=
HN
AM
(h qu ca ñnh lý Ta-lét)
⇒
HN =
AM .BH
AB
(2) 0,25
T (1) và (2)
⇒
HC = 2. HN
⇒
HN =
HC
2
d)
0,75)
⇒
N là trung ñim ca CH. 0,25
Chú ý: ðim nh$ nht trong tng phn là 0,25 ñ và ñim toàn bài không làm tròn.
HT