Bài tập xung số Svth: Nguyễn Đăng Minh Quân
-1- mquanik@yahoo.com
Bài tập xung số
3.3 Trong các biểu thứclogic dưới đây, Z=1 với tổ hợp giá trị nào của những
biến A,B,C
a.
Z AB BC AC
A
B
C
AB
BC
AC
Z AB BC AC
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
1
1
0
1
1
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
1
0
0
1
1
1
1
1
0
Vậy các tổ hợp của các biến A,B,C làm Z=1 là: 001,011,110,111
b.
Z AB BC AC
A
B
C
AB
BC
AC
Z AB BC AC
0
0
0
1
1
0
0
0
1
1
0
0
0
1
0
0
0
0
0
1
1
0
1
0
1
0
0
0
1
1
1
1
0
1
0
0
0
1
1
0
0
0
1
1
1
1
0
0
0
0
Vậy các tổ hợp của các biến A,B,C làm Z=1 là: 000,001,100,110
c.
Z AB ABC AB ABC
A
B
C
AB
ABC
AB
ABC
Z AB ABC AB ABC
0
0
0
0
1
0
0
1
0
0
1
0
0
0
0
0
0
1
0
0
0
1
0
1
0
1
1
0
0
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
0
0
0
1
1
1
0
0
0
0
1
1
1
1
1
0
0
0
0
0
Vậy các tổ hợp của các biến A,B,C làm Z=1 là: 000,010,011,100,101,110
Bài tập xung số Svth: Nguyễn Đăng Minh Quân
-2- mquanik@yahoo.com
d.
Z AB BC(A B)
A
B
C
AB
BC
AB BC
A+B
Z AB BC(A B)
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
0
1
0
0
1
1
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
1
0
0
1
1
1
1
1
0
1
1
0
1
0
1
1
1
1
0
0
1
0
Vậy các tổ hợp của các biến A,B,C làm Z=1 là: 011,100,101
3.4 Chứng minh đẳng thức sau:
a.
A BC D A.(B C).D
Cm:
VT A BC D A.BC.D A.(B C).D VP
b.
AB AB C A B C
Cm:
VT AB AB C AB.AB.C A B . A B .C
AA AB AB BB .C AB AB .C
A B .C VP
c.
A A B C A BC
Cm:
VT A A B C A A B C
A B C A B.C VP
d.
AB AB AB AB 1
Cm:
A
1
1
1
1
B
0
1
0
1
Bài tập xung số Svth: Nguyễn Đăng Minh Quân
-3- mquanik@yahoo.com
3.5 Chứng minh các đẳng thức sau
a.
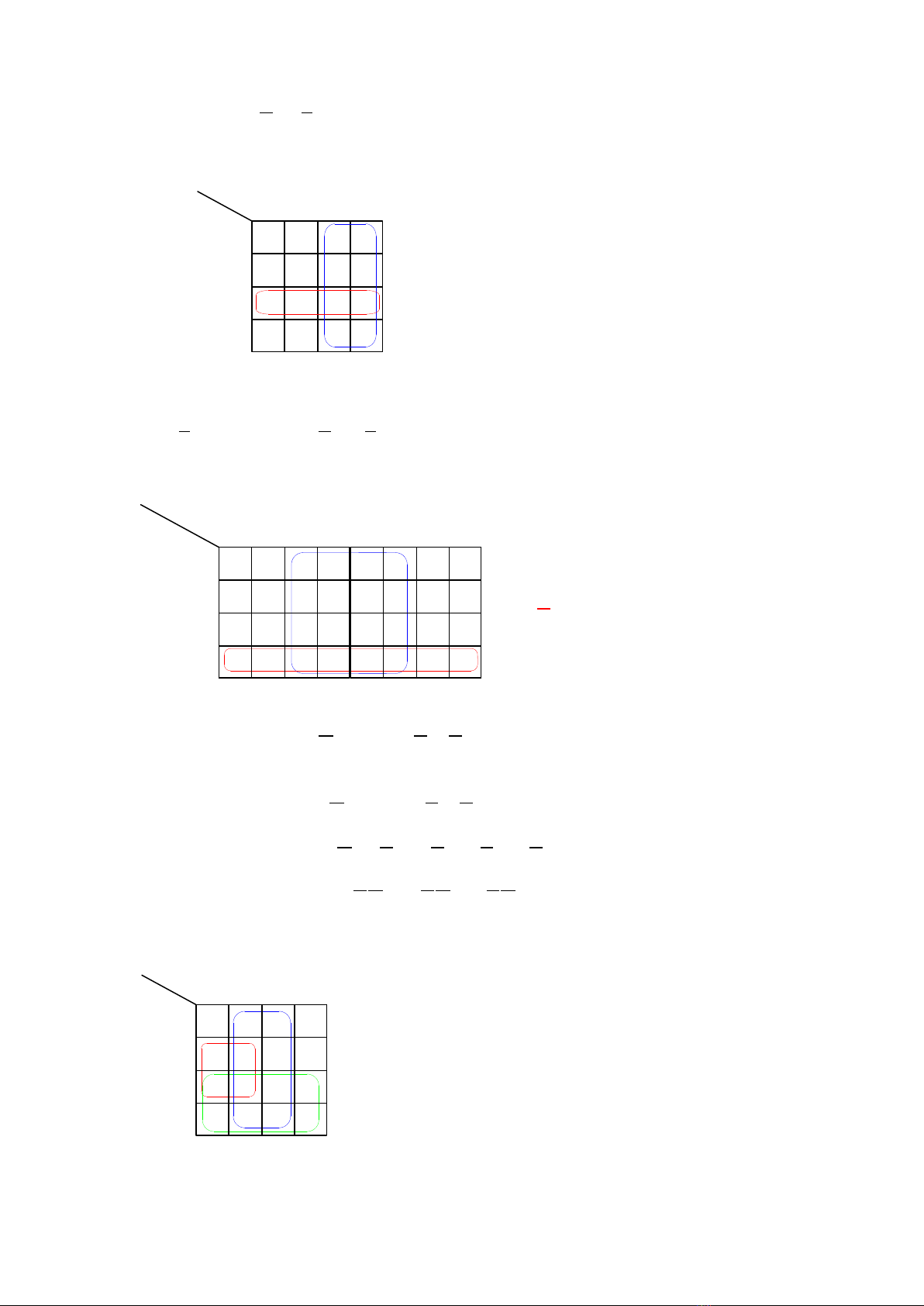
AB BCD AC BC AB C
Ta có bảng Karnaugh:
AB
C
Vậy đẳng thức đã cho là đúng.
b.
AB BD DCE DA AB D
Ta có bảng Karnaugh:
AB
D
Vậy đẳng thức đã cho là đúng.
c.
AB C D D D A B B C A BC D
Ta có:
AB C D D D A B B C A BC D
ABC ABD D D AB AC BB BC A BC D
ABC ABD D ABD ACD BCD A BC D
Ta có bảng Karnaugh:
A
BC
D
Vậy đẳng thức đã cho là đúng.
AB
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
CD
00
01
11
10
00
01
11
10
AB
0
0
1
1
0
0
1
1
0
0
1
1
1
1
1
1
CDE
000
001
011
010
00
01
11
10
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
110
111
101
100
AB
0
0
1
1
0
0
1
1
1
1
1
1
0
0
1
1
CD
00
01
11
10
00
01
11
10
Bài tập xung số Svth: Nguyễn Đăng Minh Quân
-4- mquanik@yahoo.com
d.
ABCD ABCD AB BC CD DA
Cm:
VP AB BC CD DA
A B B C C D A D
AB AC BB BC C D A D
AB AC BC C D A D
ABC ACC BCC ABD ACD BCD A D
ABC ABD ACD BCD A D
AABC AABD AACD ABCD ABCD ABDD ACDD BCDD
ABCD ABCD
VT

e.
AB BC CA AB BC CA
Cm:
AB BC CA AB BC CA
AB BC CA AB BC CA
A B B C A C A B B C A C
AB BB AC BC A C AB BB AC BC A C
AB AC BC A C AB AC BC A C
AAB AAC ABC ABC ACC BCC
AAB AAC ABC ABC ACC BCC
ABC ABC ABC ABC
Vậy đẳng thức đã được chứng minh.
f.
A B B C C D AB BC CD DA
Cm:
A B B C C D AB BC CD DA
A B B C C D AB BC CD DA
A B B C C D AB BC CD DA (2)
Thay vì chứng minh đẳng thức (1) ta chứng minh đẳng thức (2)
Bài tập xung số Svth: Nguyễn Đăng Minh Quân
-5- mquanik@yahoo.com
Ta có:
VT A B B C C D
AB AB BC BC CD CD
AB BC CD AB BC CD
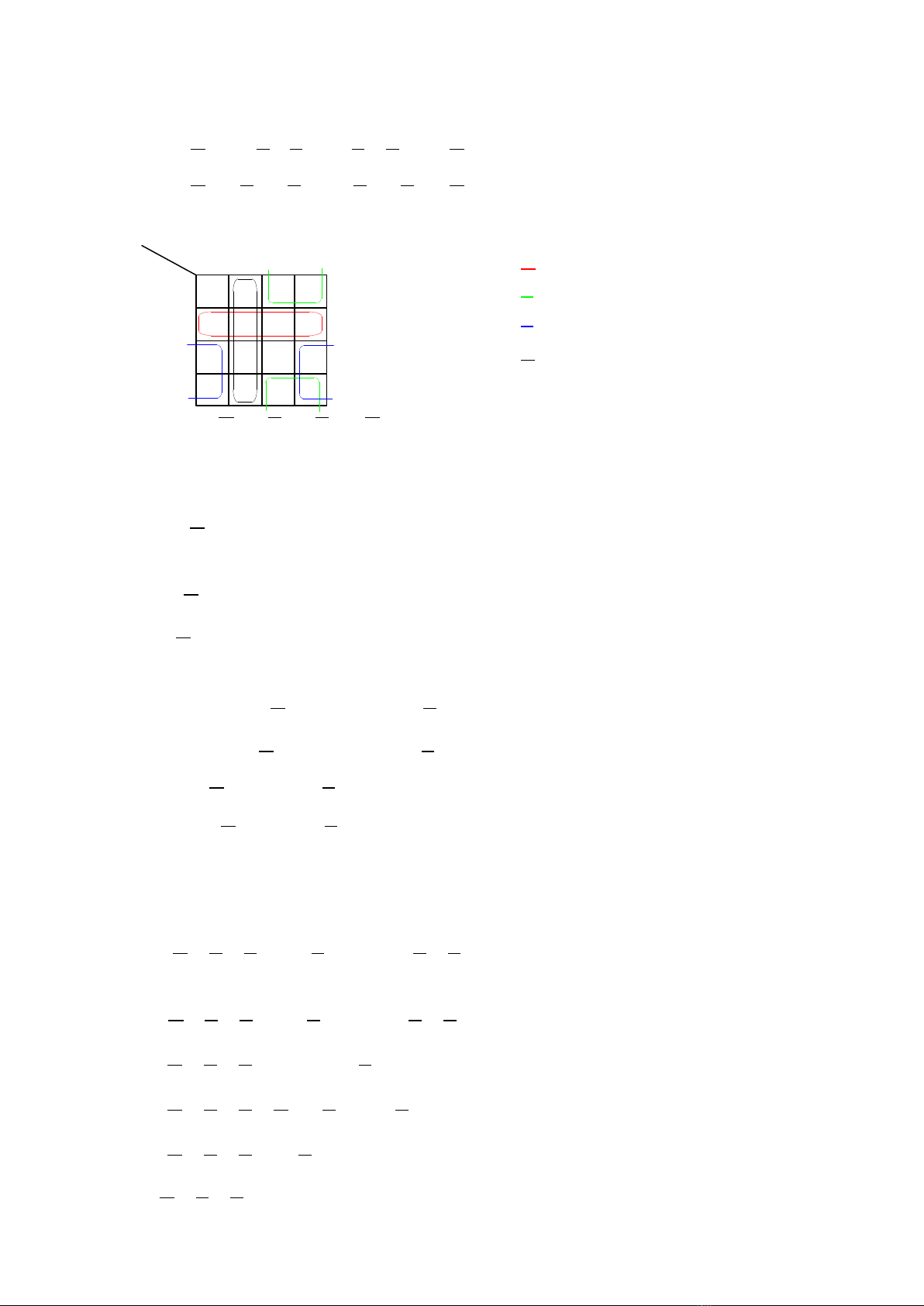
Ta có bảng Karnaugh:
AB
BC
CD
DA
VT AB BC CD DA
Vậy đẳng thức (2) đúng nên đẳng thức (1) đúng.
3.32 Tối thiểu hóa các hàm logic về dạng tối giản:
a.
A A B B B C B
Ta có:
A A B B B C B
AA AB BB BC B
AB B BC B
AB B A A BC B C C
AB AB AB BC BC BC
AB AB BC BC
B A A B C C
BB
B

b.
A B C B B C C B C
Ta có
A B C B B C C B C
A B C 1 C 1 B
A B C AC BC 1 B
A B C 1 B
A B C
AB
0
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
CD
00
01
11
10
00
01
11
10