45
dấu * là tích chập. Ảnh nhận được tại đầu ra được cho bởi:
),(
),( yxo
eyxg (4.7)
Thuật toán này sẽ làm giảm ảnh hưởng của những tín hiệu chói không đồng
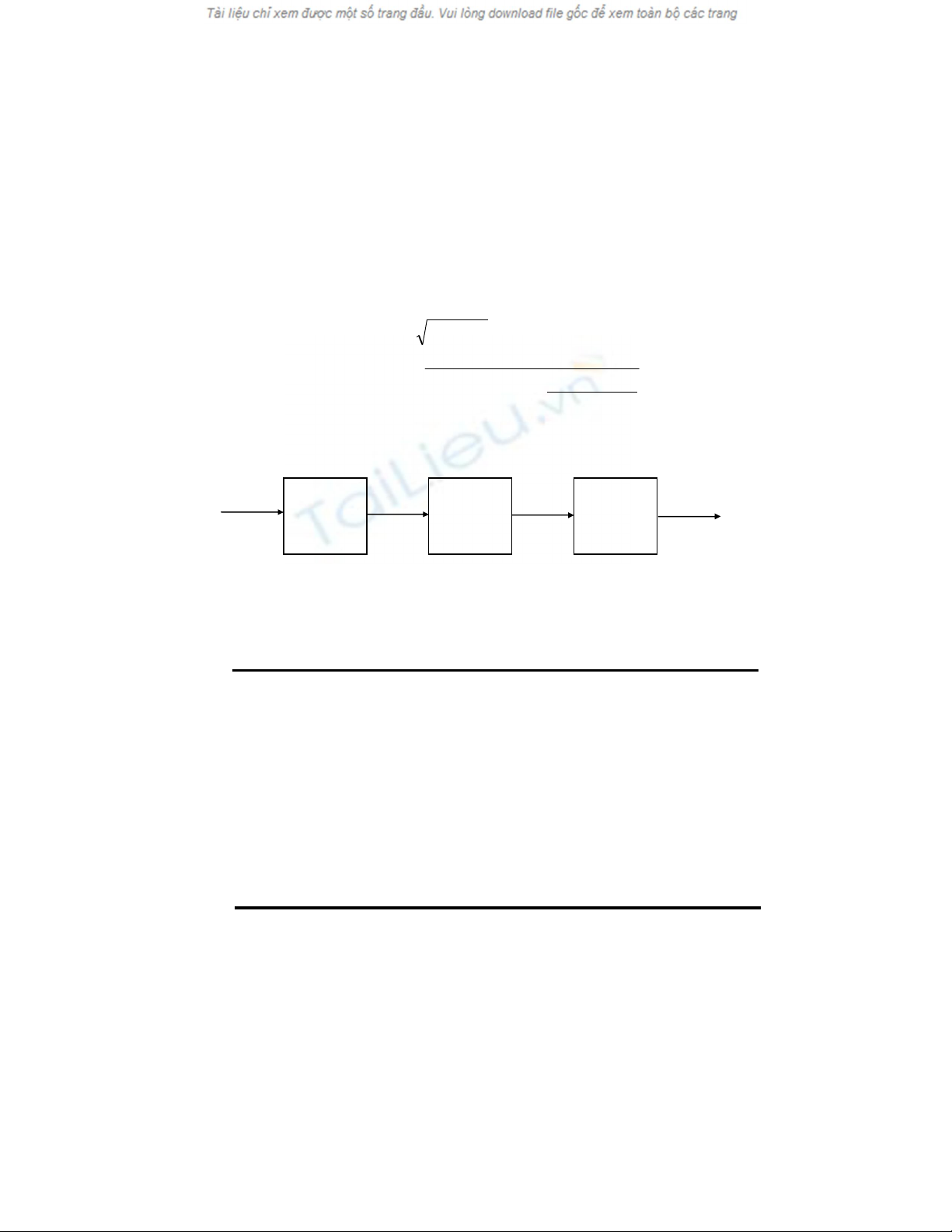
đều trong ảnh và làm nổi các chi tiết trên ảnh. Ba tham số trong hình 4.1 (H
,L ,,D0) được chọn từ thực nghiệm. Đặc tuyến trong hình 4.1 có thể được mô
tả, cho ví dụ, bằng hàm Butterworth, cho trong trường hợp này theo biểu thức:
Cho
H
LH
LH
LH
DD
D
H
)(
1
),(
),(
),( 2
0
2
21
2
21
21
các trường hợp còn lại HH
( , )
1 2
(4.8)
Hình 4.2 Lọc đồng hình.
Bảng 4.1 Các hệ số của bộ lọc 5 5 được dùng theo kiểu lọc đồng hình.
0.02675 -0.001526 -0.007420 -0.001526 -
.002675
-
0.001526 -0.034115
-0.059471 -0.034115 -
.001526
-
0.007420 -0.059471 0.902895 -0.059471 -
.007420
-
0.001526 -0.034115 -0.059471 -0.034115 -
.001526
-
0.002675 -0.001526 -0.007420 -0.001526 0.00267
5
Dùng chương trình (2.1) trong chương 2, chúng ta có thể thiết kế bộ lọc FIR
có đặc tuyến mô tả bằng biểu thức (4.8). Các hệ số của bộ lọc 5 5 có H =
1.0, L = 0.5 và D0 = 0.8 được cho ở bảng 4.1. Đáp ứng tần số được cho ở
hình 4.3.
Chương trình lọc ảnh dùng bộ lọc FIR được cho ở trong chương 3, chương
trình 3.2, có thể thay đổi thành lọc đồng hình. Chú ý rằng, nếu logarit của giá
ln[f(x,y)] H(1, 2)
eo(x ,y)
ảnh đã lọc
f(x,y)
o(x,y)
0
2
2
2
121 ),( DD
46
trị điểm ảnh đã được chuyển vào bộ đệm, thì bộ đệm chuyển ảnh trong hình
3.1 phải có kiểu "float" thay cho kiểu "unsigned char". Kết quả của chương
trình được chứa vào các biến con trỏ float thay thế cho các biến giá trị nguyên.
Trước khi lấy logarit, tốt nhất là nên chia các mức xám của ảnh đầu vào
nằm trong khoảng giữa 0.0000001 đến 10. Điều này sẽ hạn chế đầu vào với
phần chia của hệ số logarit, việc đó sẽ qui định sự phân ly giữa các giá trị
điểm, ngaọi trừ giá trị không, giá trị này sẽ là  trong hệ số logarit.
Bài tập 4.1 Thay đổi chương trình 3.2 để đưa ra bộ lọc đồng hình.
Chúng ta sẽ kiểm tra khái niệm lọc đồng hình. Hình 4.5 đưa ra một ảnh sẽ
được sử dụng để kiểm tra. Hình 4.6 trình bày một ảnh sau khi áp dụng lọc
đồng hình với bộ lọc có hệ số cho trong bảng 4.1. Bạn chú ý rằng nhiều đặc
điểm trong ảnh bây giờ trở nên rõ ràng hơn. Tuy nhiên, lọc đồng hình đã
không di chuyển một vài ảnh hưởng ánh sáng, cũng như các vùng phản chiếu
và bóng tối.
Bài tập 4.2
1. Thiết kế bộ lọc 7 7 dùng xấp xỉ hàm Butterword cho bởi biểu thức
(4.8) với H = 1.0, L= 0.25 và D0 = 0.8 và H = 1.0, L= 0.25 và D0
= 0.6 . Thiết kế bộ lọc FIR 7 7 dùng xấp xỉ hàm bộ lọc thông cao
Butterword được cho trong ví dụ 2.6 trong chương 2.
2. Dùng bộ lọc có các hệ số cho trong bảng 4.1 và thiết kế để lọc ảnh cho
trên đĩa với file có tên là "TESH.IMG".
3. Bây giờ lọc ảnh "TESH. IMG" với bộ lọc thông cao có cùng đặc tuyến.
4. Lặp lại phần 2 và 3 trên ảnh "PISTON.IMG" có sẵn trên ảnh đi kèm
5. Giải thích các kết quả khác nhau thu được từ bài tập này.
47
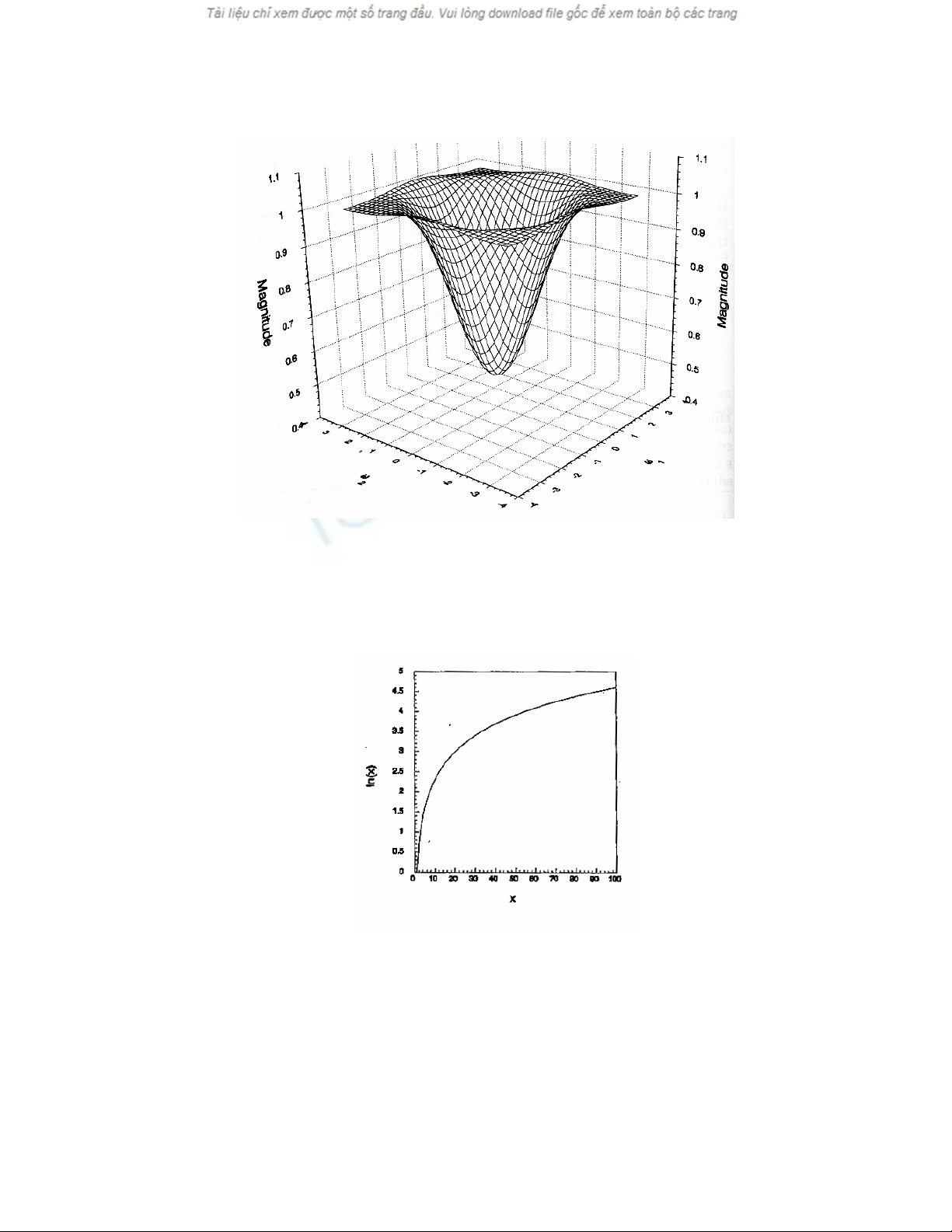
Hình 4.3 Ảnh 3-D thiết kế bộ lọc 5 5 với D0 = 0.8, L= 0.5.
Hệ số được cho trong bảng 4.1.
Hình 4.4 Đồ thị ln(x).
48
Hình 4.5 Ảnh dùng kiểm tra lọc đồng hình.
49
Hình 4.6 Ảnh đã lọc đồng hình.
4.4 Lọc pha tương phản
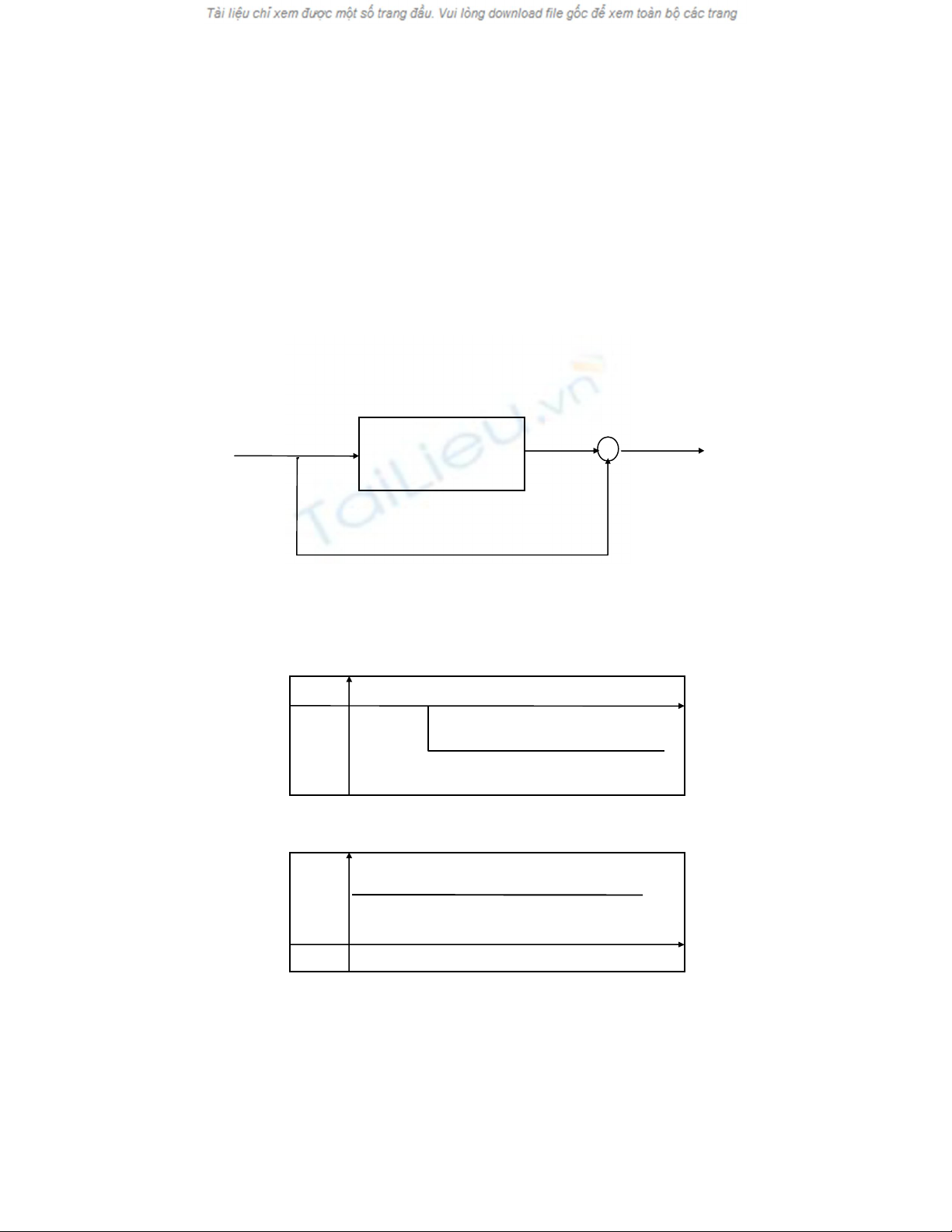
Giải pháp lọc pha tương phản được mô tả tốt nhất bằng biểu đồ hình 4.7.
Ảnh I(x,y) đi qua bộ lọc thông toàn bộ với các đặc tuyến pha mô tả ở hình 4.8.
Hình 4.7 Sơ đồ khối của lọc pha tương phản.
H(1 , 2)
I(x,y) g(x,y)
c
D(
1 ,
2)
(
1 ,
2)
1
D(
1 ,
2)
H (
1 ,
2)